2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
18. (9分)如图,网格中每个小正方形的边长为1,请你认真观察图1,2,3中阴影部分构成的图案,解答下面的问题.
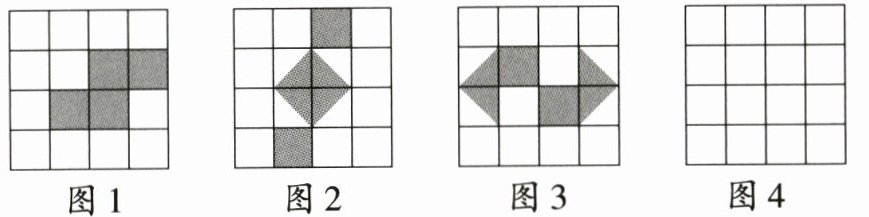
(1)这三个图案都具有以下共同特征:
①都是
②每个图案的面积均为
(2)请在图4中设计出一个具备上述特征的图案,要求所画图案不能与图1,2,3中所给出的图案相同.

(1)这三个图案都具有以下共同特征:
①都是
中心
对称图形,都不是轴
对称图形;②每个图案的面积均为
4
.(2)请在图4中设计出一个具备上述特征的图案,要求所画图案不能与图1,2,3中所给出的图案相同.
答案:
18.解:
(1)①中心 轴 (4分)
②4 (6分)
(2)所画图案如图所示.(答案不唯一) (9分)

18.解:
(1)①中心 轴 (4分)
②4 (6分)
(2)所画图案如图所示.(答案不唯一) (9分)

19. 〔南昌市〕(9分)如图,将△ABC绕着点B逆时针旋转α(0°<α<180°)得到△A′BC′,若点C′恰好落在边AC上,A′B//AC.
(1)求证:△ABC是等腰三角形;
(2)连接AA′,已知AC = 4 cm,当α = 30°时,求四边形AA′BC的面积.
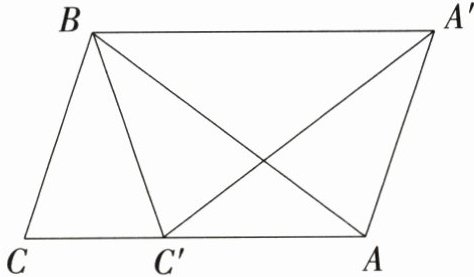
(1)求证:△ABC是等腰三角形;
(2)连接AA′,已知AC = 4 cm,当α = 30°时,求四边形AA′BC的面积.

答案:
19.解:
(1)证明:由旋转的性质,得A'B = AB,BC = BC',∠ABC = ∠A'BC'.
∴∠C = ∠BC'C. (2分)
∵A'B//AC,
∴∠A'BC' = ∠BC'C.
∴∠C = ∠ABC.
∴AB = AC.
∴△ABC是等腰三角形. (4分)
(2)过点B作BH⊥AC于点H.
根据题意,得∠ABA' = α = 30°.
∵A'B//AC,
∴∠BAC = ∠ABA' = 30°.
∵BH⊥AC,AB = AC = A'B = 4cm,
∴BH = $\frac{1}{2}$AB = 2cm. (7分)
∴S△ABC = $\frac{1}{2}$AC·BH = 4cm²,
S△ABA' = $\frac{1}{2}$A'B·BH = 4cm².
∴S四边形AA'BC = S△ABC + S△ABA' = 8cm². (9分)
(1)证明:由旋转的性质,得A'B = AB,BC = BC',∠ABC = ∠A'BC'.
∴∠C = ∠BC'C. (2分)
∵A'B//AC,
∴∠A'BC' = ∠BC'C.
∴∠C = ∠ABC.
∴AB = AC.
∴△ABC是等腰三角形. (4分)
(2)过点B作BH⊥AC于点H.
根据题意,得∠ABA' = α = 30°.
∵A'B//AC,
∴∠BAC = ∠ABA' = 30°.
∵BH⊥AC,AB = AC = A'B = 4cm,
∴BH = $\frac{1}{2}$AB = 2cm. (7分)
∴S△ABC = $\frac{1}{2}$AC·BH = 4cm²,
S△ABA' = $\frac{1}{2}$A'B·BH = 4cm².
∴S四边形AA'BC = S△ABC + S△ABA' = 8cm². (9分)
20. 〔武汉模拟〕(9分)如图,已知点A(-2,-1),B(-5,-5),C(-2,-3),P(-6,0).
(1)将△ABC绕点P逆时针旋转90°得△A₁B₁C₁,画出△A₁B₁C₁,点C的对应点C₁的坐标为
(2)画出△ABC关于原点成中心对称的图形△A₂B₂C₂,点A的对应点A₂的坐标为
(3)把△A₂B₂C₂向下平移6个单位长度得△A₃B₃C₃,画出△A₃B₃C₃,△A₃B₃C₃可由△A₁B₁C₁绕点Q逆时针旋转90°得到,画出点Q,点Q的坐标为
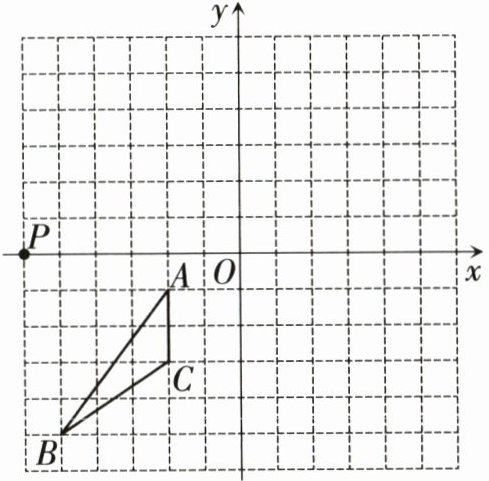
(1)将△ABC绕点P逆时针旋转90°得△A₁B₁C₁,画出△A₁B₁C₁,点C的对应点C₁的坐标为
(-3,4)
;(2)画出△ABC关于原点成中心对称的图形△A₂B₂C₂,点A的对应点A₂的坐标为
(2,1)
;(3)把△A₂B₂C₂向下平移6个单位长度得△A₃B₃C₃,画出△A₃B₃C₃,△A₃B₃C₃可由△A₁B₁C₁绕点Q逆时针旋转90°得到,画出点Q,点Q的坐标为
(3,3)
.
答案:
20.解:
(1)△A₁B₁C₁如图所示. (2分)
(-3,4) (3分)
(2)△A₂B₂C₂如图所示. (5分)
(2,1) (6分)
(3)△A₃B₃C₃和点Q如图所示. (8分)
(3,3) (9分)

20.解:
(1)△A₁B₁C₁如图所示. (2分)
(-3,4) (3分)
(2)△A₂B₂C₂如图所示. (5分)
(2,1) (6分)
(3)△A₃B₃C₃和点Q如图所示. (8分)
(3,3) (9分)

查看更多完整答案,请扫码查看


