2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
9. 如图,直角三角形$AOB$的直角顶点在坐标原点,$\angle OAB = 30^{\circ}$,若点$A$在反比例函数$y = \frac{6}{x}(x > 0)$的图象上,则经过点$B$的反比例函数图象的解析式为 (

A.$y = - \frac{6}{x}$
B.$y = - \frac{4}{x}$
C.$y = - \frac{2}{x}$
D.$y = \frac{2}{x}$
C
)
A.$y = - \frac{6}{x}$
B.$y = - \frac{4}{x}$
C.$y = - \frac{2}{x}$
D.$y = \frac{2}{x}$
答案:
9.C [解析]如图,过点B作BC⊥x轴于点C,过点A 作AD⊥x轴于点D.
∵∠BOA=90°,
∴∠BOC+∠AOD=90°.
∵∠AOD+∠OAD=90°,
∴∠BOC=∠OAD.
∵∠BCO=∠ADO=90°,
∴△BCO∽△ODA.
∵∠OAB=30°,∠BOA=90°,
∴AB=2OB,AO²+OB²=AB²,即AO²+OB²=4OB².
∴AO²=3OB².
∴$\frac{OB}{AO}$=$\frac{\sqrt{3}}{3}$,$\frac{S_{\triangle BCO}}{S_{\triangle ODA}}$=($\frac{\sqrt{3}}{3}$)²=$\frac{1}{3}$.
∵点A在反比例函数y=$\frac{6}{x}$的图象上,
∴S△ODA=$\frac{1}{2}$×6=3.
∴S△BCO=$\frac{1}{3}$S△ODA=1.设经过点B的反比例函数图象的解析式为y=$\frac{k}{x}$.
∴S△BCO=$\frac{1}{2}$|k|=1.
∴k=2或k=−2.
∵经过点B的反比例函数图象在第二象限,
∴k=−2.
∴经过点B的反比例函数图象的解析式为y=−$\frac{2}{x}$.故选C.

9.C [解析]如图,过点B作BC⊥x轴于点C,过点A 作AD⊥x轴于点D.
∵∠BOA=90°,
∴∠BOC+∠AOD=90°.
∵∠AOD+∠OAD=90°,
∴∠BOC=∠OAD.
∵∠BCO=∠ADO=90°,
∴△BCO∽△ODA.
∵∠OAB=30°,∠BOA=90°,
∴AB=2OB,AO²+OB²=AB²,即AO²+OB²=4OB².
∴AO²=3OB².
∴$\frac{OB}{AO}$=$\frac{\sqrt{3}}{3}$,$\frac{S_{\triangle BCO}}{S_{\triangle ODA}}$=($\frac{\sqrt{3}}{3}$)²=$\frac{1}{3}$.
∵点A在反比例函数y=$\frac{6}{x}$的图象上,
∴S△ODA=$\frac{1}{2}$×6=3.
∴S△BCO=$\frac{1}{3}$S△ODA=1.设经过点B的反比例函数图象的解析式为y=$\frac{k}{x}$.
∴S△BCO=$\frac{1}{2}$|k|=1.
∴k=2或k=−2.
∵经过点B的反比例函数图象在第二象限,
∴k=−2.
∴经过点B的反比例函数图象的解析式为y=−$\frac{2}{x}$.故选C.

10. 如图,在$\bigtriangleup ABC$中,$CD\perp AB$,且$CD^2 = AD · DB$,$AE$平分$\angle CAB$交$CD$于点$F$,交$BC$于点$E$,$\angle EAB = \angle B$,$CN =$
$BE$,连接$FN$.则下列结论正确的是 (
①$CF = BN$;②$\angle ACB = 90^{\circ}$;③$FN // AB$;④$AD^2 = DF · CD$.
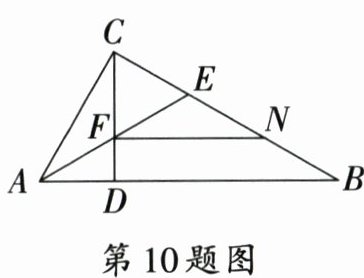
A.①②④
B.②③④
C.①②③④
D.①③
$BE$,连接$FN$.则下列结论正确的是 (
C
)①$CF = BN$;②$\angle ACB = 90^{\circ}$;③$FN // AB$;④$AD^2 = DF · CD$.

A.①②④
B.②③④
C.①②③④
D.①③
答案:
10.C [解析]
∵CD⊥AB,
∴∠ADC=∠CDB=90°.
∵CD²=AD·DB,
∴$\frac{CD}{DB}$=$\frac{AD}{CD}$.
∴△ADC∽△CDB.
∴∠ACD=∠B.
∴∠ACB=∠ACD+∠BCD=∠B +∠BCD=90°.②正确.
∵AE平分∠CAB,
∴∠EAC=∠EAB.
∵∠ACE=∠ADF=90°,
∴∠AFD=∠AEC.
∵∠AFD=∠CFE,
∴∠CFE=∠AEC.
∴CF=CE.
∵CN=BE,
∴CE=BN.
∴CF=BN.①正确.
∵∠EAB=∠B,
∴AE=BE,∠ACD=∠B=∠EAB=∠EAC.
∴AF=CF=BN.
∴EF=NE.
∴$\frac{EF}{AE}$=$\frac{NE}{BE}$.
∵∠FEN=∠AEB,
∴△EFN∽△EAB.
∴∠EFN=∠EAB.
∴FN//AB.③正确.
∵∠EAB=∠ACD,∠ADF=∠ADC,
∴△ADF∽△CDA.
∴$\frac{AD}{CD}$=$\frac{DF}{AD}$,即AD²=DF·CD.④正确.综上所述,结论正确的是①②③④.故选C.
∵CD⊥AB,
∴∠ADC=∠CDB=90°.
∵CD²=AD·DB,
∴$\frac{CD}{DB}$=$\frac{AD}{CD}$.
∴△ADC∽△CDB.
∴∠ACD=∠B.
∴∠ACB=∠ACD+∠BCD=∠B +∠BCD=90°.②正确.
∵AE平分∠CAB,
∴∠EAC=∠EAB.
∵∠ACE=∠ADF=90°,
∴∠AFD=∠AEC.
∵∠AFD=∠CFE,
∴∠CFE=∠AEC.
∴CF=CE.
∵CN=BE,
∴CE=BN.
∴CF=BN.①正确.
∵∠EAB=∠B,
∴AE=BE,∠ACD=∠B=∠EAB=∠EAC.
∴AF=CF=BN.
∴EF=NE.
∴$\frac{EF}{AE}$=$\frac{NE}{BE}$.
∵∠FEN=∠AEB,
∴△EFN∽△EAB.
∴∠EFN=∠EAB.
∴FN//AB.③正确.
∵∠EAB=∠ACD,∠ADF=∠ADC,
∴△ADF∽△CDA.
∴$\frac{AD}{CD}$=$\frac{DF}{AD}$,即AD²=DF·CD.④正确.综上所述,结论正确的是①②③④.故选C.
11. 如图,四边形$ABCD\sim$四边形$A'B'C'D'$,则$\alpha =$

83°
.
答案:
11.83°
12. 设题新角度 开放性试题 如图,已知$\angle 1 = \angle 2$,请添加一个条件:
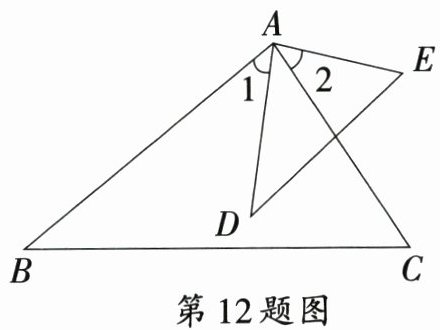
∠B=∠D(答案不唯一)
,使$\bigtriangleup ABC\sim\bigtriangleup ADE$.
答案:
12.∠B=∠D(答案不唯一)
13. 如图,四边形$ABCD$与四边形$EFGH$位似,其位似中心为点$O$,且$\frac{OE}{EA} = \frac{5}{4}$,则$\frac{EH}{AD} =$
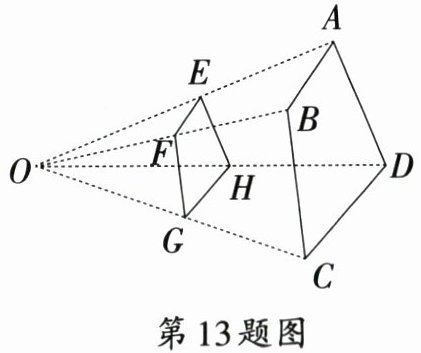
$\frac{5}{9}$
.
答案:
13.$\frac{5}{9}$
14. 小明同学想测量公园内某棵冷杉的高度$AB$,如图,他调整自己的位置,设法使自制的直角三角板$DEF$的斜边$DF$保持水平,并且边$DE$与点$B$在同一直线上.已知直角三角板的两条直角边$DE = 30 cm$,$EF = 15 cm$,测得边$DF$离地面的高度$AC = 1.6 m$,$CD = 10 m$,则冷杉$AB$高

6.6m
.
答案:
14.6.6m [解析]
∵∠DEF=∠DCB=90°,∠D=∠D,
∴△DEF∽△DCB.
∴$\frac{DE}{CD}$=$\frac{EF}{BC}$
∵DE=30cm=0.3m,EF=15cm=0.15m,CD=10m,
∴$\frac{0.3}{10}$=$\frac{0.15}{BC}$.
∴BC=5m.
∴AB=AC+BC=6.6m.
∵∠DEF=∠DCB=90°,∠D=∠D,
∴△DEF∽△DCB.
∴$\frac{DE}{CD}$=$\frac{EF}{BC}$
∵DE=30cm=0.3m,EF=15cm=0.15m,CD=10m,
∴$\frac{0.3}{10}$=$\frac{0.15}{BC}$.
∴BC=5m.
∴AB=AC+BC=6.6m.
15. 〔开封市〕如图,在$\bigtriangleup ABC$中,$\angle B = 90^{\circ}$,$AB = 6 mm$,$BC = 12 mm$,动点$P$从点$A$开始沿边$AB$向点$B$以$2 mm/s$的速度移动,动点$Q$从点$B$开始沿边$BC$向点$C$以$4 mm/s$的速度移动,如果$P$,$Q$两点同时出发,那么当$\bigtriangleup PBQ$与$\bigtriangleup ABC$相似时,$\bigtriangleup PBQ$的面积是
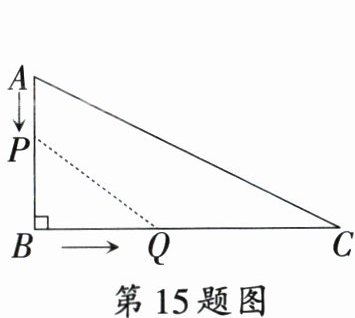
5.76或9
$ mm^2$.
答案:
15.5.76或9 [解析]设点P,Q运动的时间为ts.根据题意,得AP=2tmm,BQ=4tmm.
∴PB=(6 - 2t)mm.
∵∠PBQ=∠ABC=90°,
∴△PBQ与△ABC相似时,分两种情况:
①当△PBQ~△ABC时,$\frac{PB}{AB}$=$\frac{BQ}{BC}$,
∵AB=6mm,BC=12mm,
∴$\frac{6−2t}{6}$=$\frac{4t}{12}$.
∴t=1.5.
∴6−2t=3,4t=6.
∴PB=3mm,BQ=6mm.
∴S△PBQ=$\frac{1}{2}$PB·BQ=9mm².
②当△PBQ∽△CBA时,$\frac{PB}{BC}$=$\frac{BQ}{AB}$,
∴$\frac{6−2t}{12}$=$\frac{4t}{6}$.
∴t=0.6.
∴6−2t=4.8,4t=2.4.
∴PB=4.8mm,BQ=2.4mm.
∴S△PBQ=$\frac{1}{2}$PB·BQ=5.76mm².
综上所述,△PBQ的面积是5.76mm²或9mm².
∴PB=(6 - 2t)mm.
∵∠PBQ=∠ABC=90°,
∴△PBQ与△ABC相似时,分两种情况:
①当△PBQ~△ABC时,$\frac{PB}{AB}$=$\frac{BQ}{BC}$,
∵AB=6mm,BC=12mm,
∴$\frac{6−2t}{6}$=$\frac{4t}{12}$.
∴t=1.5.
∴6−2t=3,4t=6.
∴PB=3mm,BQ=6mm.
∴S△PBQ=$\frac{1}{2}$PB·BQ=9mm².
②当△PBQ∽△CBA时,$\frac{PB}{BC}$=$\frac{BQ}{AB}$,
∴$\frac{6−2t}{12}$=$\frac{4t}{6}$.
∴t=0.6.
∴6−2t=4.8,4t=2.4.
∴PB=4.8mm,BQ=2.4mm.
∴S△PBQ=$\frac{1}{2}$PB·BQ=5.76mm².
综上所述,△PBQ的面积是5.76mm²或9mm².
查看更多完整答案,请扫码查看


