《2026年王朝霞考点梳理时习卷九年级数学全一册人教版》

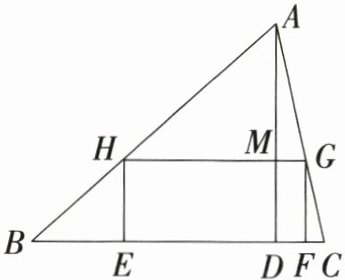
21. 课后题改编 (10分)如图所示，要在底边$BC = 160$、高$AD = 120$的$\bigtriangleup ABC$上截取一个矩形$EFGH$，使点$H$在
$AB$上，点$G$在$AC$上，点$E$，$F$在$BC$上，$AD$交$HG$于点$M$.
(1)设矩形$EFGH$的长$HG = y$、宽$HE = x$，求$y$与$x$的函数关系式.
(2)设矩形$EFGH$的面积为$S$，当$x$为何值时，矩形$EFGH$的面积$S$最大？并求出最大值.

答案： 21.解:
(1)在矩形EFGH中,HG//EF,∠HEF=90°.
∵AD是△ABC中BC边上的高，
∴∠ADB=90°.
∵AD=120,HE=x,
∴HE=MD=x,AM=AD−MD=120−x.(3分)
∵HG//EF,
∴△AHG∽△ABC.
∴$\frac{HG}{BC}$=$\frac{AM}{AD}$.
∵BC=160,
∴$\frac{y}{160}$=$\frac{120−x}{120}$,
∴y与x的函数关系式为y=−$\frac{4}{3}$x+160.　　(6分)
(2)S=xy=x(−$\frac{4}{3}$x + 160)=−$\frac{4}{3}$(x−60)²+4800.
∵−$\frac{4}{3}$＜0,
∴当x=60时,矩形EFGH的面积S最大,最大值为4800.　　　　　　　　　　　　　　　(10分)

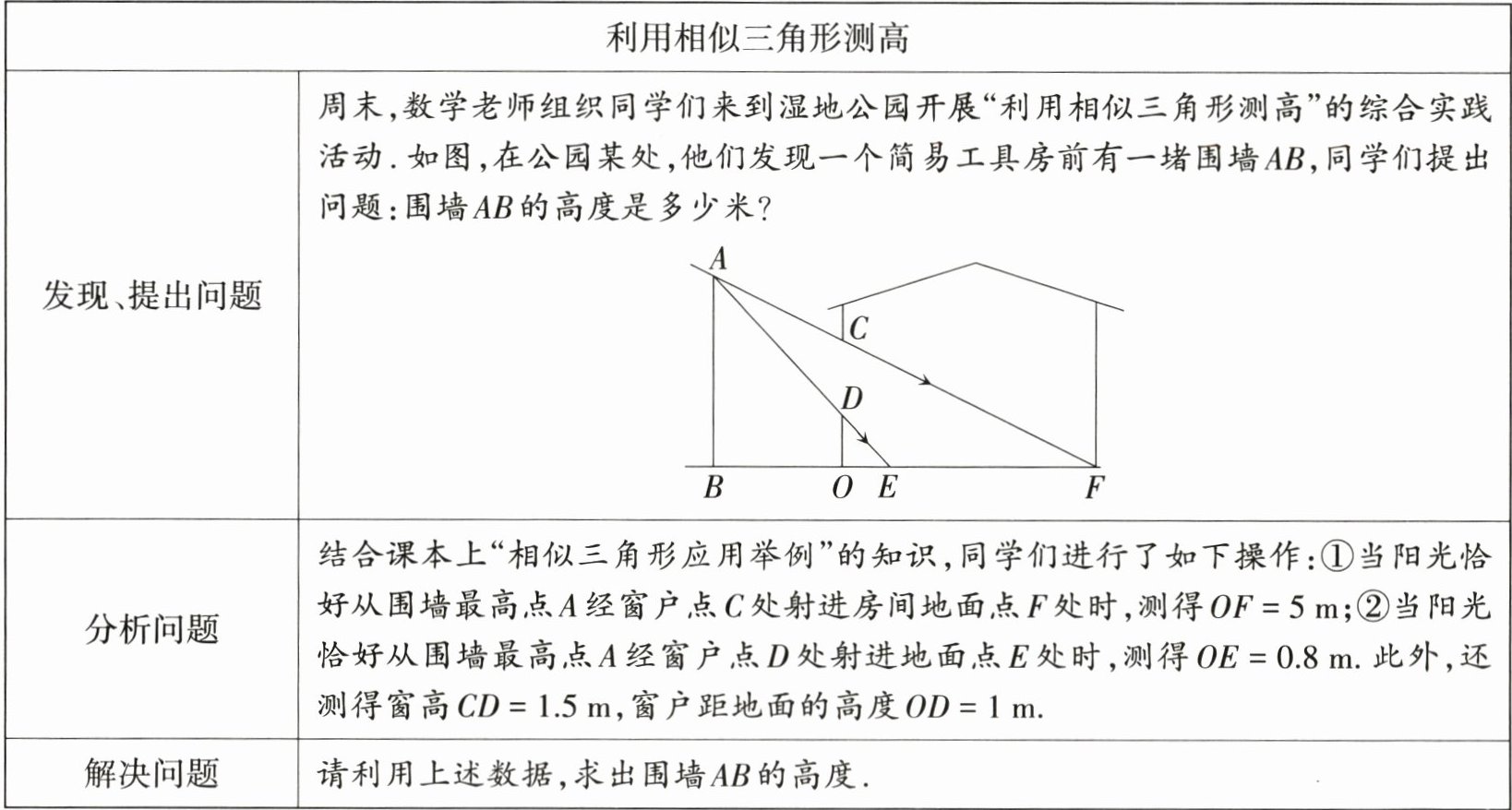
22. 设题新角度 综合与实践 (10分)根据以下材料，完成探究任务.

答案： 22.解:连接CD.
根据题意，得AB⊥BF,DO⊥BF.
∴AB//OC.
∴△ABE∽△DOE,△ABF∽△COF.　　　　(3分)
∴$\frac{AB}{OD}$=$\frac{BE}{OE}$,$\frac{AB}{CO}$=$\frac{BF}{OF}$.
∴$\frac{AB}{BE}$=$\frac{AB}{0.8}$,$\frac{AB}{1.5 + 1}$=$\frac{BF}{OF}$.
∴$\frac{5}{4}$BE=BF.
∵BF=BE+EF,EF=5−0.8=4.2m,
∴$\frac{5}{2}$BE=BE+4.2.　　　　　　　　　　　　(6分)
∴BE=2.8m.
∴AB=$\frac{5}{4}$BE=3.5m.
∴围墙AB的高度为3.5m.　　　　　　　(10分)