《2026年王朝霞考点梳理时习卷九年级数学全一册人教版》

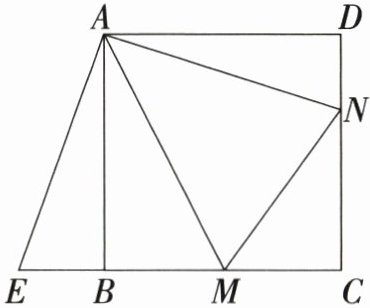
21. 教材例题改编 (10分)如图，点M，N分别在正方形ABCD的边BC，CD上，且∠MAN = 45°，把△ADN按顺时针方向旋转一定角度后得到△ABE.
(1)△ADN绕旋转中心A点，按顺时针方向旋转90°得到△ABE；
(2)求证：△AEM≌△ANM；
(3)若BM = 3，DN = 2，求正方形ABCD的边长.

答案： 21.解：
(1)A　90　　　　　　　　　　　　　　(2分)
(2)证明：由旋转的性质，得AE = AN，∠BAE = ∠DAN.
∵四边形ABCD是正方形，
∴∠BAD = 90°，即∠BAN + ∠DAN = 90°.
∴∠BAN + ∠BAE = 90°，即∠EAN = 90°.
∵∠MAN = 45°，
∴∠MAE = ∠EAN - ∠MAN = 45°.　　　　　(4分)
∴∠MAE = ∠MAN.
∵AM = AM，
∴△AEM≌△ANM.　　　　　　　　　　　(6分)
(3)设正方形ABCD的边长为x，则BC = CD = x.
∵BM = 3，DN = 2，
∴CM = BC - BM = x - 3，CN = CD - DN = x - 2.
由旋转的性质，得BE = DN = 2.
∴ME = BE + BM = 2 + 3 = 5.
由
(2)知，△AEM≌△ANM.
∴MN = ME = 5.　　　　　　　　　　　　(8分)
∵四边形ABCD是正方形，
∴∠C = 90°.
在Rt△CMN中，CM² + CN² = MN²，
即(x - 3)² + (x - 2)² = 5².
解得x = 6或x = -1(不符合题意，舍去).
∴正方形ABCD的边长为6.　　　　　　(10分)

22. (10分)问题情境：综合与实践课上，老师提出如下问题，如图1，在Rt△ABC中，∠C = 90°，AC = 6，BC = 8.将△ABC绕点A逆时针旋转得到△ADE，旋转角小于∠CAB，点B的对应点为点D，点C的对应点为点E，DE交AB于点O，延长DE交BC于点P.

　　　　　　　　
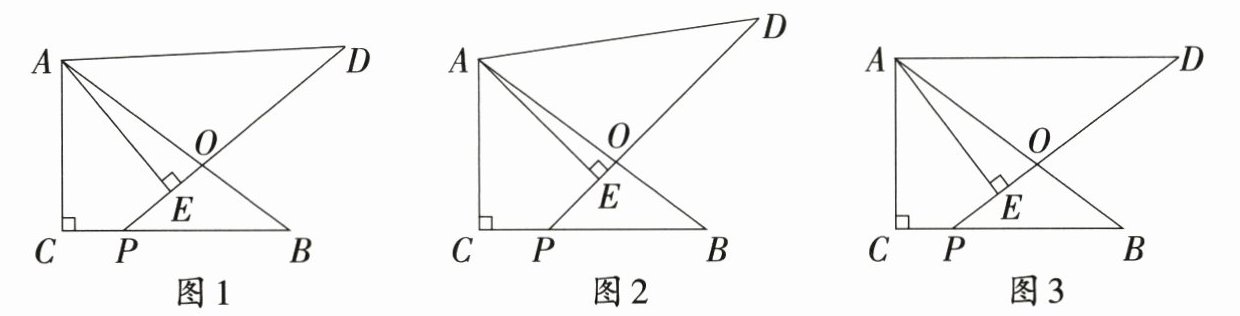
数学思考：(1)PC与PE的数量关系为PC=PE.
深入探究：(2)在以上图形旋转的过程中，老师让同学们提出新的问题.
①“乐学小组”提出问题：如图2，当∠CAE = 45°时，线段BP的长为14-6$\sqrt{2}$.
②“善思小组”提出问题：如图3，当∠CAE = ∠B时，求线段BP的长.

答案：
22.解：
(1)PC = PE　　　　　　　　　　　　　(2分)
(2)①14 - 6$\sqrt{2}$　　　　　　　　　　　　　(5分)
[解析]如图，连接AP，延长AE交BC于点F.
　　　　　　　　　
由旋转的性质知，AC = AE，∠AED = ∠C = 90°.
∴∠AEP = 90°，
∴∠C = ∠AEP.
∵AP = AP，
∴Rt△APC≌Rt△APE.
∴PC = PE.
∵∠CAE = 45°，∠C = 90°，
∴∠EFP = 45°.
∵∠AEP = 90°，
∴∠PEF = 90°.
∴∠EPF = 45°.
∴∠EPF = ∠EFP = ∠CAE.
∴PE = EF，AC = CF = 6.
设PC = PE = x，则PF = $\sqrt{PE² + EF²}$ = $\sqrt{2}$x.
∴CF = PC + PF = x + $\sqrt{2}$x = 6.
∴x = 6$\sqrt{2}$ - 6.
∴BP = BC - PC = 14 - 6$\sqrt{2}$.
②
∵∠C = 90°，AC = 6，BC = 8，
∴AB = $\sqrt{AC² + BC²}$ = 10.　　　　　　　　(6分)
由旋转的性质，得DE = BC = 8，∠D = ∠B，∠CAB = ∠EAD.
∴∠CAE = ∠B，
∴∠DAB = ∠B.
∵AD//BC，
∴∠DPB = ∠D.
∴∠DAB = ∠DPB = ∠D = ∠B.
∴AO = DO，BO = PO.　　　　　　　　　　(7分)
∵AB = AO + BO = 10，
∴PD = DO + PO = 10.
∴PE = PD - DE = 2，
∴PC = PE = 2.
∴BP = BC - PC = 6.　　　　　　　　　　(10分)