《2026年王朝霞考点梳理时习卷九年级数学全一册人教版》

8. “七巧板”是我国一种古老的益智玩具.由“七巧板”组成的正方形如图所示,若在正方形区域内随意取一点,则该点取在阴影部分的概率为(A)


A.$\frac{1}{8}$
B.$\frac{1}{7}$
C.$\frac{1}{6}$
D.$\frac{2}{7}$

答案： 8.A

9. 如图,$PA,PB$是$\odot O$的切线,$AC$是$\odot O$的直径,$\angle C=55°$,则$\angle APB$等于(A)

A.$70°$
B.$65°$
C.$60°$
D.$55°$

答案： 9.A

10. 〔新乡市〕我们定义一种新函数:形如$y=|ax^2+bx+c|(a\ne0,b^2-4ac＞0)$的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数$y=|x^2-2x-3|$的图象(如图所示),并写出下列5个结论:
①图象与坐标轴的交点为$(-1,0)$,$(3,0)$和$(0,3)$;

②图象具有对称性,对称轴是直线$x=1$;
③当$-1\leqslant x\leqslant1$或$x\geqslant3$时,函数值$y$随$x$值的增大而增大;
④当$x=-1$或$x=3$时,函数有最小值,最小值是0;
⑤当$x=1$时,函数有最大值,最大值是4.
其中正确结论的个数是(A)

A.4个
B.3个
C.2个
D.1个

答案： 10.A [解析]令$y=0$，则有$\vert x^{2}-2x-3\vert=0$。解得$x_{1}=3$，$x_{2}=-1$。$\therefore$函数$y=\vert x^{2}-2x-3\vert$的图象与$x$轴的交点坐标为$(-1,0)$，$(3,0)$。令$x=0$，得$y=3$。$\therefore$函数$y=\vert x^{2}-2x-3\vert$的图象与$y$轴的交点坐标为$(0,3)$。$\therefore$函数$y=\vert x^{2}-2x-3\vert$的图象与坐标轴的交点为$(-1,0)$，$(3,0)$和$(0,3)$。①正确。
$\because$函数$y=x^{2}-2x-3$的图象的对称轴为直线$x=1$，$\therefore$函数$y=\vert x^{2}-2x-3\vert$的图象的对称轴为直线$x=1$。②正确。由①②可知，函数$y=\vert x^{2}-2x-3\vert$的图象与$x$轴的交点坐标为$(-1,0)$，$(3,0)$，对称轴为直线$x=1$。观察函数图象可知，当$-1\leq x\leq1$或$x\geq3$时，函数值$y$随$x$值的增大而增大。③正确。观察函数图象可知，当$x=-1$或$x=3$时，函数有最小值，最小值为$0$。④正确。观察函数图象可知，函数$y=\vert x^{2}-2x-3\vert$没有最大值。⑤错误。综上所述，正确结论的个数是$4$个。故选A。

11. 设题新角度 开放性试题 写出一个开口向上,经过$(0,3)$的二次函数图象的解析式是$y=x^{2}+3($答案不唯一).

答案： 11.$y=x^{2}+3$(答案不唯一)

12. 〔南京市〕劳动教育已纳入人才培养全过程,某学校加大投入,逐年扩建劳动教育基地,校园内劳动教育基地的面积在两年内,从$300\ m^2$增加到$363\ m^2$(每年的增长率一样),设每年增长的百分率为$x$,则可列方程为$300(1+x)^{2}=363$.

答案： 12.$300(1+x)^{2}=363$

13. 跨学科 生物学 人类的性别由一对染色体决定,称为性染色体.女性的性染色体是一对同型的染色体,用$XX$表示,男性的性染色体是一对异型的染色体,用$XY$表示,每个人的成对染色体每次只有一个能遗传给后代,且可能性相等,则一对夫妇的第一个孩子是女孩的概率是$\frac{1}{2}$.

答案： 13.$\frac{1}{2}$

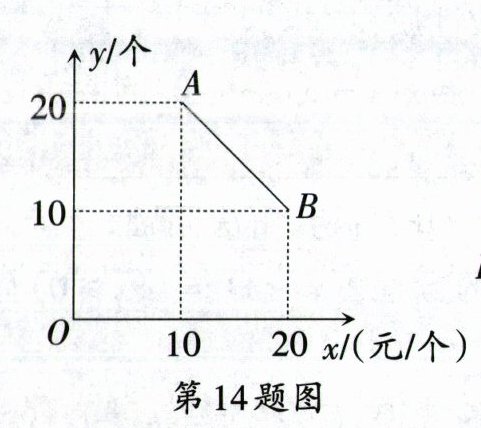
14. 某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量$y$(个)与销售价格$x$(元/个)的关系如图所示.当$10\leqslant x\leqslant20$时,其图象是线段$AB$,则该食品零售店每天销售这款冷饮产品的最大利润为121元(利润$=$总销售额$-$总成本).

答案： 14.121 [解析]当$10\leq x\leq20$时，设线段$AB$的解析式为$y=kx+b$。把点$(10,20)$，$(20,10)$代入，得$\begin{cases}10k + b = 20\\20k + b = 10\end{cases}$，解得$\begin{cases}k = -1\\b = 30\end{cases}$。
$\therefore$当$10\leq x\leq20$时，每天的销售量$y$与销售价格$x$的函数解析式为$y=-x + 30$。
设该食品零售店每天销售这款冷饮产品的利润为$w$元。
根据题意，得$w=(x - 8)y=(x - 8)(-x + 30)=-x^{2}+38x - 240=-(x - 19)^{2}+121$。
$\because -1\lt0$，$\therefore$当$x = 19$时，$w$有最大值，最大值为$121$。

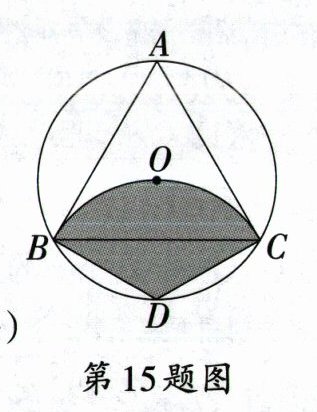
15. 〔河南中考〕如图,$\odot O$是边长为$4\sqrt{3}$的等边三角形$ABC$的外接圆,点$D$是$\widehat{BC}$的中点,连接$BD,CD$.以点$D$为圆心,$BD$的长为半径在$\odot O$内画弧,则阴影部分的面积为$\frac{16\pi}{3}$.

答案： 15.$\frac{16\pi}{3}$ [解析]连接$OD$交$BC$于点$E$。
$\because D$是$\overset{\frown}{BC}$的中点，$\therefore BD = CD$。
$\therefore OD\perp BC$，$BE=\frac{1}{2}BC = 2\sqrt{3}$。
$\because\triangle ABC$为等边三角形，且内接于$\odot O$，
$\therefore\angle BAC = 60^{\circ}$。$\therefore\angle BDC = 180^{\circ}-\angle BAC = 120^{\circ}$。$\therefore\angle DBC=\frac{1}{2}(180^{\circ}-\angle BDC)=30^{\circ}$。
$\therefore BD = 2DE$。由勾股定理，得$BD^{2}=DE^{2}+BE^{2}$，即$4DE^{2}=DE^{2}+12$。
$\therefore DE = 2$。$\therefore BD = 4$。
$\therefore S_{阴影}=\frac{120\pi×4^{2}}{360}=\frac{16\pi}{3}$。