2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
7. [唐山市]如图,$ Rt\triangle ABC$中,$\angle C = 90^{\circ}$,点$D$在$AC$上,$\angle DBC = \angle A$.若$AC = 4$,$\cos A = \frac{4}{5}$,则$BD =$ (
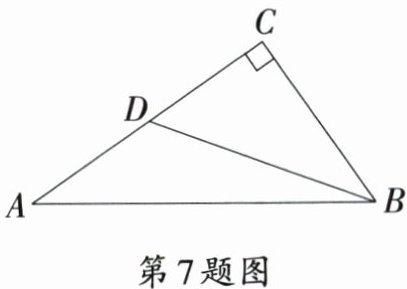
A.$\frac{9}{4}$
B.$\frac{12}{5}$
C.$\frac{15}{4}$
D.$4$
C
)
A.$\frac{9}{4}$
B.$\frac{12}{5}$
C.$\frac{15}{4}$
D.$4$
答案:
7.C
8. 中华优秀传统文化情境 榫卯 榫卯是古代中国建筑、家具及其他器械的主要结构方式.如图,在某燕尾榫中,榫槽的横截面$ABCD$是梯形,其中$AD // BC$,$AB = DC$,燕尾角$\angle B = \alpha$,外口宽$AD = a$,榫槽深度是$b$,则它的里口宽$BC$为 (

A.$\frac{b}{\tan\ \alpha} + a$
B.$\frac{2b}{\tan\ \alpha} + a$
C.$b\tan\ \alpha + a$
D.$2b\tan\ \alpha + a$
B
)
A.$\frac{b}{\tan\ \alpha} + a$
B.$\frac{2b}{\tan\ \alpha} + a$
C.$b\tan\ \alpha + a$
D.$2b\tan\ \alpha + a$
答案:
8.B
9. 如图,在$\triangle ABC$中,$\angle BAC = 120^{\circ}$,$\angle ACB = 20^{\circ}$,$\angle ACB$的平分线与$\angle BAC$的邻补角平分线交于点$D$,连接$BD$,则$\tan\angle BDC$的值是 (
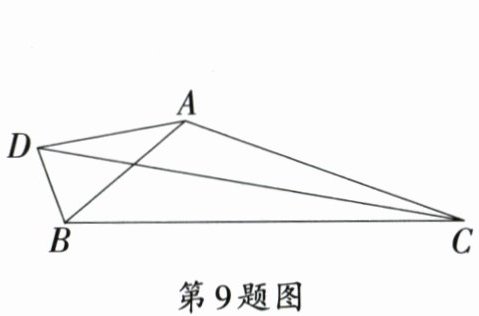
A.$1$
B.$\frac{1}{2}$
C.$\sqrt{3}$
D.$\frac{\sqrt{3}}{3}$
C
)
A.$1$
B.$\frac{1}{2}$
C.$\sqrt{3}$
D.$\frac{\sqrt{3}}{3}$
答案:
9.C [解析]如图,过点D分别作CA,AB,CB所在直线的垂线,垂足分别为E,F,G.

∵∠ACB的平分线与∠BAC的邻补角平分线交于点D,
∴DE=DF=DG,∠ABD=$\frac{1}{2}$∠ABG,∠BCD=$\frac{1}{2}$∠ACB.
∵∠BAC=120°,∠ACB=20°,
∴∠ABC=40°.
∴∠ABG=140°.
∴∠ABD=$\frac{1}{2}$∠ABG =70°.
∴∠DBC=∠ABD+∠ABC=110°.
∵∠BCD=$\frac{1}{2}$∠ACB=10°,
∴∠BDC=180°−∠DBC−∠BCD=60°.
∴tan∠BDC=$\sqrt{3}$.故选C.
9.C [解析]如图,过点D分别作CA,AB,CB所在直线的垂线,垂足分别为E,F,G.

∵∠ACB的平分线与∠BAC的邻补角平分线交于点D,
∴DE=DF=DG,∠ABD=$\frac{1}{2}$∠ABG,∠BCD=$\frac{1}{2}$∠ACB.
∵∠BAC=120°,∠ACB=20°,
∴∠ABC=40°.
∴∠ABG=140°.
∴∠ABD=$\frac{1}{2}$∠ABG =70°.
∴∠DBC=∠ABD+∠ABC=110°.
∵∠BCD=$\frac{1}{2}$∠ACB=10°,
∴∠BDC=180°−∠DBC−∠BCD=60°.
∴tan∠BDC=$\sqrt{3}$.故选C.
10. 如图,在平面直角坐标系$xOy$中,$AB = 2\sqrt{10}$,延长$AB$至点$C$,连接$OC$.若满足$OC^2 = BC · AC$,$\tan\alpha = 3$,则点$C$的坐标为 (
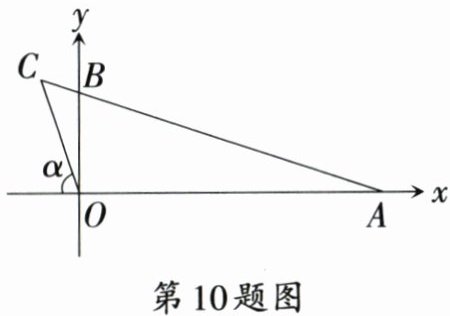
A.$\left( - \frac{3}{4}, \frac{9}{4}\right)$
B.$(-3,9)$
C.$(-2,6)$
D.$\left( - \frac{5}{3}, \frac{15}{4}\right)$
A
)
A.$\left( - \frac{3}{4}, \frac{9}{4}\right)$
B.$(-3,9)$
C.$(-2,6)$
D.$\left( - \frac{5}{3}, \frac{15}{4}\right)$
答案:
10.A [解析]如图,过点C作CD⊥x轴,垂足为点D.

∵OC²=BC·AC,
∴$\frac{OC}{AC}$=$\frac{BC}{OC}$.
∵∠ACO=∠BCO,
∴△COA∽△CBO.
∴∠CAO=∠COB.
∵∠COB+∠COD=90°,∠CAO+∠ABO=90°,
∴∠COD=∠ABO=α.
∵tanα=3,
∴tan∠ABO=$\frac{AO}{BO}$=3.
∴AO=3BO.在Rt△ABO中,
∵AO²+BO²=AB²,
∴9BO²+BO²=40.
∴BO=2.
∴AO=3BO=6.在Rt△CDO中,tanα=$\frac{CD}{DO}$=3,
∴CD=3DO.
∵∠CDO=∠BOA=90°,∠BAO=∠CAD,
∴△BAO ∽△CAD.
∴$\frac{BO}{CD}$=$\frac{AO}{AD}$
∴$\frac{2}{3DO}$=$\frac{6}{6 + DO}$
∴DO=$\frac{3}{4}$
∴CD=3DO=$\frac{9}{4}$.故选A.
10.A [解析]如图,过点C作CD⊥x轴,垂足为点D.

∵OC²=BC·AC,
∴$\frac{OC}{AC}$=$\frac{BC}{OC}$.
∵∠ACO=∠BCO,
∴△COA∽△CBO.
∴∠CAO=∠COB.
∵∠COB+∠COD=90°,∠CAO+∠ABO=90°,
∴∠COD=∠ABO=α.
∵tanα=3,
∴tan∠ABO=$\frac{AO}{BO}$=3.
∴AO=3BO.在Rt△ABO中,
∵AO²+BO²=AB²,
∴9BO²+BO²=40.
∴BO=2.
∴AO=3BO=6.在Rt△CDO中,tanα=$\frac{CD}{DO}$=3,
∴CD=3DO.
∵∠CDO=∠BOA=90°,∠BAO=∠CAD,
∴△BAO ∽△CAD.
∴$\frac{BO}{CD}$=$\frac{AO}{AD}$
∴$\frac{2}{3DO}$=$\frac{6}{6 + DO}$
∴DO=$\frac{3}{4}$
∴CD=3DO=$\frac{9}{4}$.故选A.
11. 如果$\cos A = \frac{\sqrt{3}}{2}$,那么锐角$\angle A$的度数为
30°
.
答案:
11.30°
12. [南京模拟]如图,在一坡度为$1 : 2$的斜坡上种有两棵树,它们之间的距离($AB$)为$10\ m$,则这两棵树的高度差($BC$)为
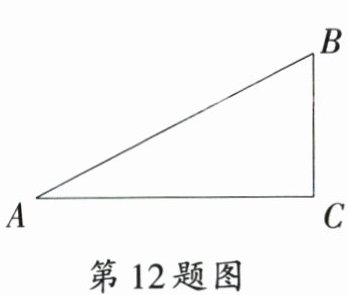
4.47
$ m$.($\sqrt{5} \approx 2.236$,结果精确到$0.01$)
答案:
12.4.47
13. 如图,点$A$,$B$,$C$在正方形网格的格点(网格线的交点)上,则$\sin\angle BAC =$

$\frac{\sqrt{26}}{26}$
.
答案:
13.$\frac{\sqrt{26}}{26}$
14. 一副三角板按如图方式摆放,其中$\angle ADB = \angle BCD = 90^{\circ}$,$\angle A = 60^{\circ}$,$\angle CBD = 45^{\circ}$,$E$为$AB$的中点,过点$E$作$EF \perp CD$于点$F$.若$AD = 4\ cm$,则$EF$的长为
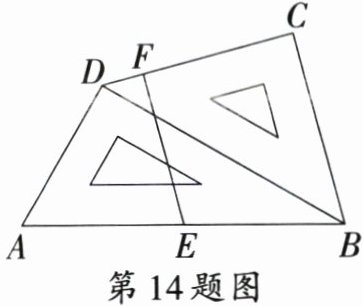
($\sqrt{6}$+$\sqrt{2}$)
$ cm$.
答案:
14.($\sqrt{6}$+$\sqrt{2}$)
查看更多完整答案,请扫码查看


