2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
1. 中华优秀传统文化情境 纹样 纹样是我国古代艺术中的瑰宝.下列四幅纹样图形既是轴对称图形又是中心对称图形的是
(

(
B
)
答案:
B
2. 方程$x^2 = 3x$的解为
(
A.$x_1 = x_2 = 0$
B.$x_1 = x_2 = 3$
C.$x_1 = x_2 = -3$
D.$x_1 = 0$,$x_2 = 3$
(
D
)A.$x_1 = x_2 = 0$
B.$x_1 = x_2 = 3$
C.$x_1 = x_2 = -3$
D.$x_1 = 0$,$x_2 = 3$
答案:
D
3. 抛物线$y = 2(x - 1)^2 - 3$向左平移2个单位长度,再向上平移5个单位长度,所得的抛物线的解析式为
(
A.$y = 2(x + 1)^2 + 2$
B.$y = 2(x - 1)^2 + 2$
C.$y = 2(x + 1)^2 - 2$
D.$y = 2(x - 1)^2 - 2$
(
A
)A.$y = 2(x + 1)^2 + 2$
B.$y = 2(x - 1)^2 + 2$
C.$y = 2(x + 1)^2 - 2$
D.$y = 2(x - 1)^2 - 2$
答案:
A
4. 用配方法解方程$x^2 + 4x = 1$,变形后的结果正确的是
(
A.$(x + 2)^2 = 3$
B.$(x + 4)^2 = 3$
C.$(x + 2)^2 = 5$
D.$(x + 4)^2 = 5$
(
C
)A.$(x + 2)^2 = 3$
B.$(x + 4)^2 = 3$
C.$(x + 2)^2 = 5$
D.$(x + 4)^2 = 5$
答案:
C
5. 如图,将$\triangle OAB$绕点$O$逆时针旋转$60°$得到$\triangle OCD$,连接$BD$,$AC$.若$OA = 4$,$\angle AOB = 35°$,则下列结论不一定正确的是
(
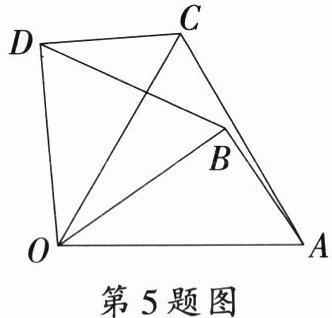
A.$\angle BDO = 60°$
B.$\angle BOC = 25°$
C.$OC = 4$
D.$CD // OA$
(
D
)
A.$\angle BDO = 60°$
B.$\angle BOC = 25°$
C.$OC = 4$
D.$CD // OA$
答案:
D
6. 已知二次函数$y = ax^2 + bx + c$的图象如图所示,那么下列结论中正确的是
(
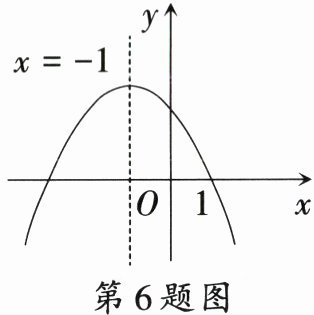
A.$ac > 0$
B.$b > 0$
C.$a + c < 0$
D.$a + b + c = 0$
(
D
)
A.$ac > 0$
B.$b > 0$
C.$a + c < 0$
D.$a + b + c = 0$
答案:
D
7. 已知关于$x$的一元二次方程$x^2 + (2m + 1)x + m - 1 = 0$的两个根分别是$x_1$,$x_2$,且满足$x_1^2 + x_2^2 = 3$,则$m$的值是
(
A.0
B.-2
C.0或$-\frac{1}{2}$
D.-2或0
(
C
)A.0
B.-2
C.0或$-\frac{1}{2}$
D.-2或0
答案:
C
8.〔唐山市〕如图,将一个小球从斜坡的点$O$处抛出,小球的抛出路线可以用抛物线$y = 4x - \frac{1}{2}x^2$刻画,斜坡可以用直线$y = \frac{1}{2}x$刻画.下列结论错误的是
(
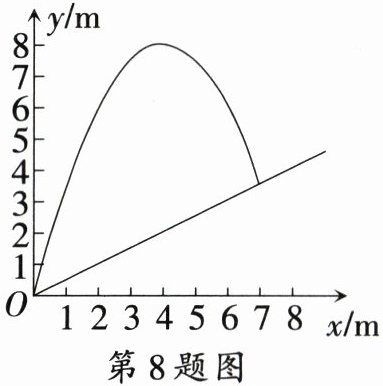
A.小球落地点与点$O$的水平距离为7 m
B.当小球抛出高度达到7.5 m时,小球与点$O$的水平距离为3 m
C.小球与点$O$的水平距离超过4 m时呈下降趋势
D.小球与斜坡的距离的最大值为$\frac{49}{8}$m
(
B
)
A.小球落地点与点$O$的水平距离为7 m
B.当小球抛出高度达到7.5 m时,小球与点$O$的水平距离为3 m
C.小球与点$O$的水平距离超过4 m时呈下降趋势
D.小球与斜坡的距离的最大值为$\frac{49}{8}$m
答案:
B [解析]令4x−$\frac{1}{2}$x²=$\frac{1}{2}$x,解得x₁ = 0,x₂ = 7。
∴小球落地点与点O的水平距离为7m。A正确,不符合题意。把y = 7.5代入y = 4x−$\frac{1}{2}$x²,得4x−$\frac{1}{2}$x² = 7.5,解得x₁ = 3,x₂ = 5。
∴当小球抛出高度达到7.5m时,小球与点O的水平距离为3m或5m。B错误,符合题意。
∵y = 4x−$\frac{1}{2}$x² = −$\frac{1}{2}$(x−4)² + 8,
∴抛物线的对称轴为直线x = 4。
∵−$\frac{1}{2}$<0,
∴当x>4时,y随x的增大而减小。
∴小球与点O的水平距离超过4m时呈下降趋势。C正确,不符合题意。设抛物线上一点A的坐标为(a,4a−$\frac{1}{2}$a²)(0 ≤ a ≤ 7),过点A作AB⊥x轴,交直线y = $\frac{1}{2}$x于点B,则点B(a,$\frac{1}{2}$a)。
∴AB = 4a−$\frac{1}{2}$a²−$\frac{1}{2}$a = −$\frac{1}{2}$a² + $\frac{7}{2}$a = −$\frac{1}{2}$(a−$\frac{7}{2}$)² + $\frac{49}{8}$。
∵−$\frac{1}{2}$<0,
∴当a = $\frac{7}{2}$时,AB有最大值,最大值为$\frac{49}{8}$。
∴小球与斜坡的距离的最大值为$\frac{49}{8}$m。D正确,不符合题意。故选B。
∴小球落地点与点O的水平距离为7m。A正确,不符合题意。把y = 7.5代入y = 4x−$\frac{1}{2}$x²,得4x−$\frac{1}{2}$x² = 7.5,解得x₁ = 3,x₂ = 5。
∴当小球抛出高度达到7.5m时,小球与点O的水平距离为3m或5m。B错误,符合题意。
∵y = 4x−$\frac{1}{2}$x² = −$\frac{1}{2}$(x−4)² + 8,
∴抛物线的对称轴为直线x = 4。
∵−$\frac{1}{2}$<0,
∴当x>4时,y随x的增大而减小。
∴小球与点O的水平距离超过4m时呈下降趋势。C正确,不符合题意。设抛物线上一点A的坐标为(a,4a−$\frac{1}{2}$a²)(0 ≤ a ≤ 7),过点A作AB⊥x轴,交直线y = $\frac{1}{2}$x于点B,则点B(a,$\frac{1}{2}$a)。
∴AB = 4a−$\frac{1}{2}$a²−$\frac{1}{2}$a = −$\frac{1}{2}$a² + $\frac{7}{2}$a = −$\frac{1}{2}$(a−$\frac{7}{2}$)² + $\frac{49}{8}$。
∵−$\frac{1}{2}$<0,
∴当a = $\frac{7}{2}$时,AB有最大值,最大值为$\frac{49}{8}$。
∴小球与斜坡的距离的最大值为$\frac{49}{8}$m。D正确,不符合题意。故选B。
查看更多完整答案,请扫码查看


