2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
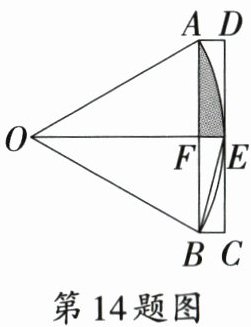
14. [河南中考]我国魏晋时期数学家刘徽在为《九章算术》作注时,创立了“割圆术”.如图是研究“割 圆术”时的一个图形,$\overgroup{AB}$所在圆的圆心为点$O$,四边形$ABCD$为矩形,边$CD$与$\odot O$相切于点$E$,连 接$BE$,$\angle ABE = 15^{\circ}$,连接$OE$交$AB$于点$F$.若$AB = 4$,则图中阴影部分的面积为
$\frac{4\pi}{3}-2\sqrt{3}$
.
答案:
14.$\frac{4\pi}{3}-2\sqrt{3}$ [解析]
∵边CD与⊙O相切于点E,
∴OE⊥CD.
∵四边形ABCD为矩形,
∴AB//CD.
∴OE⊥AB.
∴AF = BF = $\frac{1}{2}$AB = 2.
∵∠ABE = 15°,
∴∠AOE = 30°.
∴OA = 2AF = 4.
∴OF = $\sqrt{OA^{2}-AF^{2}}=2\sqrt{3}$.
∴$S_{阴影}=S_{扇形OAE}-S_{\triangle AFO}=\frac{30×\pi×4^{2}}{360}-\frac{1}{2}×2×2\sqrt{3}=\frac{4\pi}{3}-2\sqrt{3}$.
∵边CD与⊙O相切于点E,
∴OE⊥CD.
∵四边形ABCD为矩形,
∴AB//CD.
∴OE⊥AB.
∴AF = BF = $\frac{1}{2}$AB = 2.
∵∠ABE = 15°,
∴∠AOE = 30°.
∴OA = 2AF = 4.
∴OF = $\sqrt{OA^{2}-AF^{2}}=2\sqrt{3}$.
∴$S_{阴影}=S_{扇形OAE}-S_{\triangle AFO}=\frac{30×\pi×4^{2}}{360}-\frac{1}{2}×2×2\sqrt{3}=\frac{4\pi}{3}-2\sqrt{3}$.
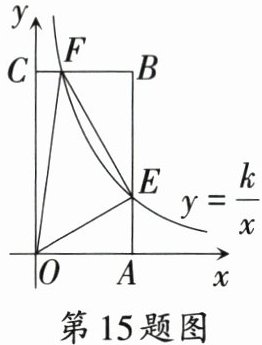
15. 如图,矩形$OABC$中,点$A(1,0)$,$C(0,2)$,反比例函数$y = \frac{k}{x} (0 < k < 2,x > 0)$的图象分别交$AB$, $CB$于点$E$,$F$,连接$OE$,$OF$,$EF$.若$S_{\triangle OEF} = 2S_{\triangle BEF}$,则$k$的值为
$\frac{2}{3}$
,点$F$的横坐标 为$\frac{1}{3}$
.
答案:
15.$\frac{2}{3}$,$\frac{1}{3}$ [解析]
∵四边形OABC是矩形,点A(1,0),C(0,2),
∴点B的坐标为(1,2),点E的坐标为(1,k),点F的坐标为$(\frac{k}{2},2)$.则$S_{\triangle BEF}=\frac{1}{2}(1-\frac{k}{2})(2 - k)=\frac{k^{2}}{4}-k + 1$,$S_{\triangle OFC}=S_{\triangle OAE}=\frac{1}{2}k$.
∴$S_{\triangle OEF}=S_{矩形OABC}-S_{\triangle OFC}-S_{\triangle OAE}-S_{\triangle BEF}=1×2-\frac{1}{2}k-\frac{1}{2}k-(\frac{k^{2}}{4}-k + 1)=-\frac{k^{2}}{4}+1$.
∵$S_{\triangle OEF}=2S_{\triangle BEF}$,
∴$-\frac{k^{2}}{4}+1=2(\frac{k^{2}}{4}-k + 1)$.整理,得$3k^{2}-8k + 4 = 0$.解得$k_{1}=2$(舍去),$k_{2}=\frac{2}{3}$.
∴$k=\frac{2}{3}$.
∴点F的横坐标为$\frac{1}{3}$.
∵四边形OABC是矩形,点A(1,0),C(0,2),
∴点B的坐标为(1,2),点E的坐标为(1,k),点F的坐标为$(\frac{k}{2},2)$.则$S_{\triangle BEF}=\frac{1}{2}(1-\frac{k}{2})(2 - k)=\frac{k^{2}}{4}-k + 1$,$S_{\triangle OFC}=S_{\triangle OAE}=\frac{1}{2}k$.
∴$S_{\triangle OEF}=S_{矩形OABC}-S_{\triangle OFC}-S_{\triangle OAE}-S_{\triangle BEF}=1×2-\frac{1}{2}k-\frac{1}{2}k-(\frac{k^{2}}{4}-k + 1)=-\frac{k^{2}}{4}+1$.
∵$S_{\triangle OEF}=2S_{\triangle BEF}$,
∴$-\frac{k^{2}}{4}+1=2(\frac{k^{2}}{4}-k + 1)$.整理,得$3k^{2}-8k + 4 = 0$.解得$k_{1}=2$(舍去),$k_{2}=\frac{2}{3}$.
∴$k=\frac{2}{3}$.
∴点F的横坐标为$\frac{1}{3}$.
16. ($10$分)解方程:
(1)[福州市]$x^2 + 2x - 5 = 0$;
(2)[山西中考]$2(x - 3)^2 = x^2 - 9$.
(1)[福州市]$x^2 + 2x - 5 = 0$;
(2)[山西中考]$2(x - 3)^2 = x^2 - 9$.
答案:
16.解:
(1)移项,得$x^{2}+2x = 5$.
配方,得$x^{2}+2x + 1 = 5 + 1$,即$(x + 1)^{2}= 6$.
由此可得$x + 1 = \pm\sqrt{6}$.
解得$x_{1}=-1+\sqrt{6}$,$x_{2}=-1-\sqrt{6}$.
(2)移项,得$2(x - 3)^{2}-(x^{2}-9)=0$,
即$2(x - 3)^{2}-(x + 3)(x - 3)=0$.
因式分解,得$(x - 3)(2x - 6 - x - 3)=0$,
即$(x - 3)(x - 9)=0$.
∴$x - 3 = 0$,或$x - 9 = 0$.
解得$x_{1}=3$,$x_{2}=9$.
(1)移项,得$x^{2}+2x = 5$.
配方,得$x^{2}+2x + 1 = 5 + 1$,即$(x + 1)^{2}= 6$.
由此可得$x + 1 = \pm\sqrt{6}$.
解得$x_{1}=-1+\sqrt{6}$,$x_{2}=-1-\sqrt{6}$.
(2)移项,得$2(x - 3)^{2}-(x^{2}-9)=0$,
即$2(x - 3)^{2}-(x + 3)(x - 3)=0$.
因式分解,得$(x - 3)(2x - 6 - x - 3)=0$,
即$(x - 3)(x - 9)=0$.
∴$x - 3 = 0$,或$x - 9 = 0$.
解得$x_{1}=3$,$x_{2}=9$.
17. [唐山市]($8$分)如图,一次函数$y = kx + b$的图象与反比例函数$y = \frac{m}{x}$的图象相交于点$A(-2,1)$、点$B(1,n)$.
(1)求一次函数和反比例函数的解析式;
(2)请直接写出关于$x$的不等式$kx + b - \frac{m}{x} < 0$的解集.
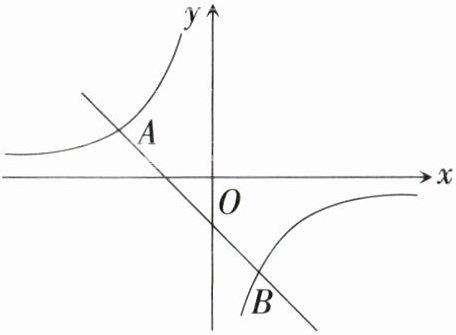
(1)求一次函数和反比例函数的解析式;
(2)请直接写出关于$x$的不等式$kx + b - \frac{m}{x} < 0$的解集.

答案:
17.解:
(1)将点A(-2,1)代入$y=\frac{m}{x}$,得$1=\frac{m}{-2}$.
解得$m = -2$.
∴反比例函数的解析式为$y=-\frac{2}{x}$.
将点B(1,n)代入$y=-\frac{2}{x}$,得$n = -2$.
∴点B(1,-2).
将点A(-2,1),B(1,-2)分别代入$y=kx + b$,
得$\begin{cases}-2k + b = 1\\k + b = -2\end{cases}$,解得$\begin{cases}k = -1\\b = -1\end{cases}$.
∴一次函数的解析式为$y=-x - 1$.
(2)关于$x$的不等式$kx + b-\frac{m}{x}<0$的解集为$-2<x<0$或$x>1$.
(1)将点A(-2,1)代入$y=\frac{m}{x}$,得$1=\frac{m}{-2}$.
解得$m = -2$.
∴反比例函数的解析式为$y=-\frac{2}{x}$.
将点B(1,n)代入$y=-\frac{2}{x}$,得$n = -2$.
∴点B(1,-2).
将点A(-2,1),B(1,-2)分别代入$y=kx + b$,
得$\begin{cases}-2k + b = 1\\k + b = -2\end{cases}$,解得$\begin{cases}k = -1\\b = -1\end{cases}$.
∴一次函数的解析式为$y=-x - 1$.
(2)关于$x$的不等式$kx + b-\frac{m}{x}<0$的解集为$-2<x<0$或$x>1$.
查看更多完整答案,请扫码查看


