2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
15.[河南中考] 如图,在$ Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CA = CB = 3$,线段CD绕点C在平面内旋转,过点B作AD的垂线,交射线AD于点E. 若$CD = 1$,则AE的最大值为
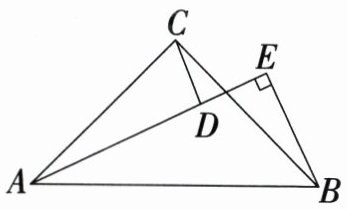
$2\sqrt{2}+1$
,最小值为$2\sqrt{2}-1$
.
答案:
15.$2\sqrt{2}+1$ $2\sqrt{2}-1$
一题多解
方法一:
∵线段CD绕点C在平面内旋转的过程中,BE始终与射线AD垂直,
∴点D在以C为圆心的圆上运动,点E的运动轨迹是以AB为直径的圆上的一段弧.如图①,过点A作⊙C的切线AD、$AD_{1}$,当点D旋转至与$D_{1}$重合时,AE取得最大值,即为线段$AE_{1}$的长度;当点D旋转至与点$D_{2}$重合时,AE取得最小值,即为线段$AE_{2}$的长度.


当点D与点$D_{1}$重合时,$AD_{1}$⊥$CD_{1}$,过点C作CF⊥BE,交$BE_{1}$的延长线于点F,如图②,则∠$AD_{1}C$ = ∠$CD_{1}E_{1}$ = ∠BFC = ∠$AE_{1}F$ = 90°.
∴四边形$CDE_{1}F$为矩形.
∴∠$FCD_{1}$ = 90°.
∵$CD_{1}$ = 1,
∴$AD_{1}$ = $\sqrt{CA^{2}-CD_{1}^{2}}$ = $2\sqrt{2}$.
∵∠ACB = 90°,
∴∠$ACD_{1}$ + ∠$BCD_{1}$ = ∠$BCD_{1}$ + ∠BCF = 90°.
∴∠$ACD_{1}$ = ∠BCF.
∵CA = CB = 3,
∴△$ACD_{1}$≌△BCF.
∴$CD_{1}$ = CF = $DE_{1}$ = 1.
∴$AE_{1}$ = $AD_{1}$ + $DE_{1}$ = $2\sqrt{2}+1$,即AE的最大值为$2\sqrt{2}+1$.
当点D与点$D_{2}$重合时,$AD_{2}$⊥$CD_{2}$,过点C作$CG\perp BE_{2}$于点G,如图③,则∠$AD_{2}C$ = ∠$BGC$ = ∠$CGE_{2}$ = ∠$BE_{2}D_{2}$ = 90°.
∴四边形$CDE_{2}G$为矩形.∠$GCD_{2}$ = 90°.
∵$CD_{2}$ = 1,
∴$AD_{2}$ = $\sqrt{CA^{2}-CD_{2}^{2}}$ = $2\sqrt{2}$.同理可得,△$ACD_{2}$≌△BCG.

∴$CD_{2}$ = CG = $D_{2}E_{2}$ = 1.
∴$AE_{2}$ = $AD_{2}$ - $D_{2}E_{2}$ = $2\sqrt{2}-1$,即AE的最小值为$2\sqrt{2}-1$.
方法二:AE取得最大值、最小值时点D、E所在位置同方法一.
∵∠ACB = 90°,CA = CB = 3,
∴∠BAC = ∠ABC = 45°.当点D与点$D_{1}$重合时,
∵∠ACB = 90°,BE⊥AD,
∴点A、C、$E_{1}$、B均在以AB为直径的圆上.连接$CE_{1}$,如图④,
则∠$AD_{1}C$ = ∠$CD_{1}E_{1}$ = 90°.
∵∠$AE_{1}C$与∠ABC都是AC所对的圆周角,
∴∠$AE_{1}C$ = ∠ABC = 45°.
∴∠$D_{1}CE_{1}$ = ∠$AE_{1}C$ = 45°.
∴$D_{1}E_{1}$ = $CD_{1}$ = 1.
∵$AD_{1}$ = $\sqrt{CA^{2}-CD_{1}^{2}}$ = $2\sqrt{2}$,
∴$AE_{1}$ = $AD_{1}$ + $D_{1}E_{1}$ = $2\sqrt{2}+1$,即AE的最大值为$2\sqrt{2}+1$.当点D与点$D_{2}$重合时,
∵∠ACB = 90°,
$BE_{2}$⊥$AD_{2}$,
∴点A、C、$E_{2}$、B均在以AB为直径的圆上.连接$CE_{2}$,如图⑤,则∠$BE_{2}D_{2}$ = ∠$AD_{2}C$ = 90°.
∵∠$BE_{2}C$与∠BAC都是BC所对的圆周角,
∴∠$BE_{2}C$ = ∠BAC = 45°.
∴∠$CE_{2}D_{2}$ = 90° - ∠$BE_{2}C$ = 45°.
∴∠$D_{2}CE_{2}$ = ∠$CE_{2}D_{2}$ = 45°.
∴$D_{2}E_{2}$ = $CD_{2}$ = 1.
∵$AD_{2}$ = $\sqrt{CA^{2}-CD_{2}^{2}}$ = $2\sqrt{2}$,
∴$AE_{2}$ = $AD_{2}$ - $D_{2}E_{2}$ = $2\sqrt{2}-1$,即AE的最小值为$2\sqrt{2}-1$.


15.$2\sqrt{2}+1$ $2\sqrt{2}-1$
一题多解
方法一:
∵线段CD绕点C在平面内旋转的过程中,BE始终与射线AD垂直,
∴点D在以C为圆心的圆上运动,点E的运动轨迹是以AB为直径的圆上的一段弧.如图①,过点A作⊙C的切线AD、$AD_{1}$,当点D旋转至与$D_{1}$重合时,AE取得最大值,即为线段$AE_{1}$的长度;当点D旋转至与点$D_{2}$重合时,AE取得最小值,即为线段$AE_{2}$的长度.


当点D与点$D_{1}$重合时,$AD_{1}$⊥$CD_{1}$,过点C作CF⊥BE,交$BE_{1}$的延长线于点F,如图②,则∠$AD_{1}C$ = ∠$CD_{1}E_{1}$ = ∠BFC = ∠$AE_{1}F$ = 90°.
∴四边形$CDE_{1}F$为矩形.
∴∠$FCD_{1}$ = 90°.
∵$CD_{1}$ = 1,
∴$AD_{1}$ = $\sqrt{CA^{2}-CD_{1}^{2}}$ = $2\sqrt{2}$.
∵∠ACB = 90°,
∴∠$ACD_{1}$ + ∠$BCD_{1}$ = ∠$BCD_{1}$ + ∠BCF = 90°.
∴∠$ACD_{1}$ = ∠BCF.
∵CA = CB = 3,
∴△$ACD_{1}$≌△BCF.
∴$CD_{1}$ = CF = $DE_{1}$ = 1.
∴$AE_{1}$ = $AD_{1}$ + $DE_{1}$ = $2\sqrt{2}+1$,即AE的最大值为$2\sqrt{2}+1$.
当点D与点$D_{2}$重合时,$AD_{2}$⊥$CD_{2}$,过点C作$CG\perp BE_{2}$于点G,如图③,则∠$AD_{2}C$ = ∠$BGC$ = ∠$CGE_{2}$ = ∠$BE_{2}D_{2}$ = 90°.
∴四边形$CDE_{2}G$为矩形.∠$GCD_{2}$ = 90°.
∵$CD_{2}$ = 1,
∴$AD_{2}$ = $\sqrt{CA^{2}-CD_{2}^{2}}$ = $2\sqrt{2}$.同理可得,△$ACD_{2}$≌△BCG.

∴$CD_{2}$ = CG = $D_{2}E_{2}$ = 1.
∴$AE_{2}$ = $AD_{2}$ - $D_{2}E_{2}$ = $2\sqrt{2}-1$,即AE的最小值为$2\sqrt{2}-1$.
方法二:AE取得最大值、最小值时点D、E所在位置同方法一.
∵∠ACB = 90°,CA = CB = 3,
∴∠BAC = ∠ABC = 45°.当点D与点$D_{1}$重合时,
∵∠ACB = 90°,BE⊥AD,
∴点A、C、$E_{1}$、B均在以AB为直径的圆上.连接$CE_{1}$,如图④,
则∠$AD_{1}C$ = ∠$CD_{1}E_{1}$ = 90°.
∵∠$AE_{1}C$与∠ABC都是AC所对的圆周角,
∴∠$AE_{1}C$ = ∠ABC = 45°.
∴∠$D_{1}CE_{1}$ = ∠$AE_{1}C$ = 45°.
∴$D_{1}E_{1}$ = $CD_{1}$ = 1.
∵$AD_{1}$ = $\sqrt{CA^{2}-CD_{1}^{2}}$ = $2\sqrt{2}$,
∴$AE_{1}$ = $AD_{1}$ + $D_{1}E_{1}$ = $2\sqrt{2}+1$,即AE的最大值为$2\sqrt{2}+1$.当点D与点$D_{2}$重合时,
∵∠ACB = 90°,
$BE_{2}$⊥$AD_{2}$,
∴点A、C、$E_{2}$、B均在以AB为直径的圆上.连接$CE_{2}$,如图⑤,则∠$BE_{2}D_{2}$ = ∠$AD_{2}C$ = 90°.
∵∠$BE_{2}C$与∠BAC都是BC所对的圆周角,
∴∠$BE_{2}C$ = ∠BAC = 45°.
∴∠$CE_{2}D_{2}$ = 90° - ∠$BE_{2}C$ = 45°.
∴∠$D_{2}CE_{2}$ = ∠$CE_{2}D_{2}$ = 45°.
∴$D_{2}E_{2}$ = $CD_{2}$ = 1.
∵$AD_{2}$ = $\sqrt{CA^{2}-CD_{2}^{2}}$ = $2\sqrt{2}$,
∴$AE_{2}$ = $AD_{2}$ - $D_{2}E_{2}$ = $2\sqrt{2}-1$,即AE的最小值为$2\sqrt{2}-1$.


16. (8分)如图,AB为⊙O的直径,$PD$切⊙O于点C,交AB的延长线于点D,且$CO = CD$,求$\angle PCA$的度数.
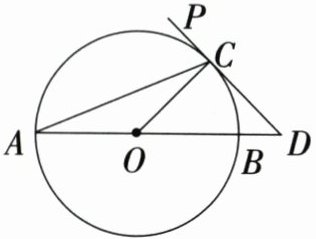

答案:
16.解:
∵PD是⊙O的切线,
∴∠OCD = 90°.(2分)
∵CO = CD,
∴∠D = ∠COD = 45°.
∵OA = OC,
∴∠CAD = ∠ACO.
∴∠CAD = $\frac{1}{2}$∠COD = 22.5°.
∴∠PCA = ∠CAD + ∠D = 67.5°.(8分)
∵PD是⊙O的切线,
∴∠OCD = 90°.(2分)
∵CO = CD,
∴∠D = ∠COD = 45°.
∵OA = OC,
∴∠CAD = ∠ACO.
∴∠CAD = $\frac{1}{2}$∠COD = 22.5°.
∴∠PCA = ∠CAD + ∠D = 67.5°.(8分)
17. 中华优秀传统文化情境 司南(9分)司南(图1)是我国古代辨别方向用的一种仪器,出现在战国时期. 司南中心为一圆形,圆心为点O,直径为20,根据八个方位将圆形八等分(图2中点A~H),过点E的⊙O的切线与AG的延长线交于点M,连接EG.
(1)相邻两个方位间所夹的圆心角的度数为
(2)求线段$AG$,$ME$的长.

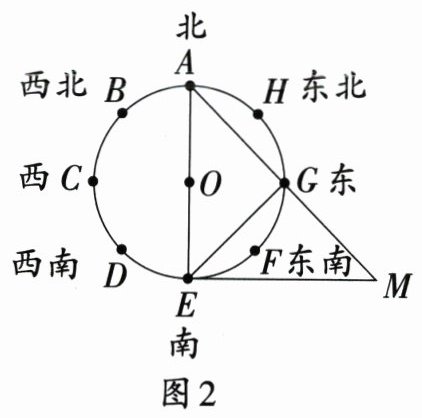
(1)相邻两个方位间所夹的圆心角的度数为
45°
;(2)求线段$AG$,$ME$的长.


答案:
17.解:
(1)45°
(2)
∵AE为⊙O的直径,
∴∠AGE = 90°.
∵AG = EG,
∴∠GAE = ∠AEG = 45°,AG = EG.
在Rt△AGE中,$AG^{2}+EG^{2}=AE^{2}$,AE = 20,
∴AG = $10\sqrt{2}$.
∵ME为⊙O的切线,
∴∠AEM = 90°.
∴∠AME = 45°.
∴∠AME = ∠EAM.
∴ME = AE = 20.(9分)
(1)45°
(2)
∵AE为⊙O的直径,
∴∠AGE = 90°.
∵AG = EG,
∴∠GAE = ∠AEG = 45°,AG = EG.
在Rt△AGE中,$AG^{2}+EG^{2}=AE^{2}$,AE = 20,
∴AG = $10\sqrt{2}$.
∵ME为⊙O的切线,
∴∠AEM = 90°.
∴∠AME = 45°.
∴∠AME = ∠EAM.
∴ME = AE = 20.(9分)
18. (9分)如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.
(1)正方形ABCD与正六边形AEFCGH的边长之比为
(2)连接BE,BE是否为⊙O的内接正n边形的一边? 如果是,求出n的值;如果不是,请说明理由.
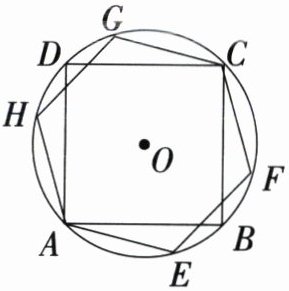
(1)正方形ABCD与正六边形AEFCGH的边长之比为
$\sqrt{2}$:1
;(2)连接BE,BE是否为⊙O的内接正n边形的一边? 如果是,求出n的值;如果不是,请说明理由.

答案:
18.解:
(1)$\sqrt{2}$:1
(2)BE是⊙O的内接正n边形的一边.(4分)
连接OA,OB,OE.
∵在正方形ABCD中,∠AOB = 90°,
在正六边形AEFCGH中,∠AOE = 60°,
∴∠BOE = 30°.(7分)
∴n = $\frac{360°}{30°}$ = 12.
∴BE是⊙O的内接正十二边形的一边.(9分)
(1)$\sqrt{2}$:1
(2)BE是⊙O的内接正n边形的一边.(4分)
连接OA,OB,OE.
∵在正方形ABCD中,∠AOB = 90°,
在正六边形AEFCGH中,∠AOE = 60°,
∴∠BOE = 30°.(7分)
∴n = $\frac{360°}{30°}$ = 12.
∴BE是⊙O的内接正十二边形的一边.(9分)
19. (9分)某蔬菜基地搭建了一座圆弧形蔬菜棚,跨度$AB = 3.2$ m,拱高$CD = 0.8$ m(C为AB的中点,D为弧AB的中点).
(1)求该圆弧所在圆的半径;
(2)在距蔬菜棚的一端0.4 m处竖立支撑杆EF,求支撑杆EF的高度.
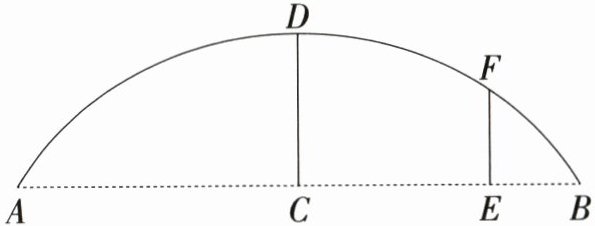
(1)求该圆弧所在圆的半径;
(2)在距蔬菜棚的一端0.4 m处竖立支撑杆EF,求支撑杆EF的高度.

答案:
19.解:
(1)如图,设圆弧AB所在圆的圆心为O,连接OD,OB.
∵D为弧AB的中点,
∴OD经过弦AB的中点,
即O,C,D三点共线.
∴BC = $\frac{1}{2}$AB = 1.6m.(2分)
设⊙O的半径为rm,则OC = (r - 0.8)m.
∵在Rt△OBC中,$OB^{2}=OC^{2}+BC^{2}$,
∴$r^{2}=(r - 0.8)^{2}+1.6^{2}$.
解得r = 2.
∴圆弧所在圆的半径为2m.(4分)

(2)过点O作OH⊥EF,交FE的延长线于点H,连接OF.
∴∠H = 90°.
∵CD⊥AB,EF⊥AB,
∴∠OCE = ∠CEH = ∠DCE = ∠CEF = 90°.
∴四边形OCEH为矩形.
∴OC = EH,OH = CE.
根据题意,得BE = 0.4m,OF = 2m.
∴OH = CE = BC - BE = 1.2m.
在Rt△OHF中,$HF=\sqrt{OF^{2}-OH^{2}} = 1.6$m.
∵HE = OC = OD - CD = 1.2m,
∴EF = HF - HE = 0.4m.
∴支撑杆EF的高度为0.4m.(9分)
19.解:
(1)如图,设圆弧AB所在圆的圆心为O,连接OD,OB.
∵D为弧AB的中点,
∴OD经过弦AB的中点,
即O,C,D三点共线.
∴BC = $\frac{1}{2}$AB = 1.6m.(2分)
设⊙O的半径为rm,则OC = (r - 0.8)m.
∵在Rt△OBC中,$OB^{2}=OC^{2}+BC^{2}$,
∴$r^{2}=(r - 0.8)^{2}+1.6^{2}$.
解得r = 2.
∴圆弧所在圆的半径为2m.(4分)

(2)过点O作OH⊥EF,交FE的延长线于点H,连接OF.
∴∠H = 90°.
∵CD⊥AB,EF⊥AB,
∴∠OCE = ∠CEH = ∠DCE = ∠CEF = 90°.
∴四边形OCEH为矩形.
∴OC = EH,OH = CE.
根据题意,得BE = 0.4m,OF = 2m.
∴OH = CE = BC - BE = 1.2m.
在Rt△OHF中,$HF=\sqrt{OF^{2}-OH^{2}} = 1.6$m.
∵HE = OC = OD - CD = 1.2m,
∴EF = HF - HE = 0.4m.
∴支撑杆EF的高度为0.4m.(9分)
查看更多完整答案,请扫码查看


