《2026年王朝霞考点梳理时习卷九年级数学全一册人教版》

23. 设题新角度 综合与实践 (11分)综合与实践课上,老师让同学们以“图形的变换”为主题开展数学活动.
(1) 操作判断
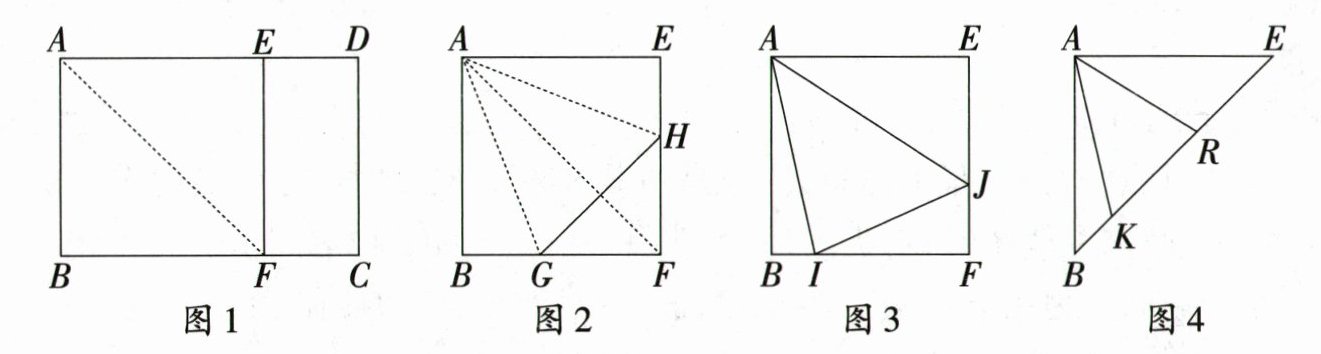
如图1,将矩形纸片$ABCD$折叠,使$AB$落在边$AD$上,点$B$与点$E$重合,折痕为$AF$,即可得到正方形$AEFB$,沿$EF$剪开,将正方形$AEFB$折叠使边$AB,AE$都落在正方形的对角线$AF$上,折痕为$AG,AH$,连接$GH$,如图2.根据以上操作,则$\angle GAH=$45$°$.
(2) 迁移探究
将图2中的$\angle GAH$绕点$A$顺时针旋转,使它的两边分别交边$BF,FE$于点$I,J$,连接$IJ$,如图3.
试猜想线段$BI,IJ,EJ$之间的数量关系,并说明理由.
(3) 拓展应用
连接正方形对角线$BE$,若图3中的$\angle IAJ$的边$AI,AJ$分别交对角线$BE$于点$K,R$,将正方形纸片沿对角线$BE$剪开,如图4.若$BK=2,ER=4$,请直接写出$KR$的长.

答案：
23.解：
(1)$45$(2分)
(2)$IJ = EJ + BI$。(3分)
理由：如图，将$\triangle AEJ$顺时针旋转$90^{\circ}$得到$\triangle ABJ'$。

由旋转的性质，得$AJ = AJ'$，$EJ = BJ'$，$\angle EAJ=\angle BAJ'$。
$\because$四边形$AEFB$为正方形，
$\therefore\angle BAE = 90^{\circ}$。(5分)
由
(1)中结论可得$\angle IAJ = 45^{\circ}$。
$\therefore\angle BAI+\angle EAJ = 45^{\circ}$。
$\therefore\angle BAJ'+\angle BAI = 45^{\circ}$。
$\therefore\angle IAJ=\angle IAJ'$。
$\because AI = AI$，$\therefore\triangle AIJ\cong\triangle AIJ'$。
$\therefore IJ = IJ'$。
$\because IJ' = BJ'+BI$，
$\therefore IJ = EJ + BI$。(9分)
(3)$KR = 2\sqrt{5}$。(11分)
[解析]如图，将$\triangle AER$绕点$A$顺时针旋转$90^{\circ}$得到$\triangle ABR'$，连接$KR'$。

根据旋转的性质，得$\angle E=\angle ABR' = 45^{\circ}$，$ER = BR'$。
与
(2)同理，可得$\triangle AKR'\cong\triangle AKR$。
$\therefore KR = KR'$。
$\because\angle E = 45^{\circ}$，$\therefore\angle ABE = 90^{\circ}-\angle E = 45^{\circ}$。
$\therefore\angle KBR'=\angle ABE+\angle ABR' = 90^{\circ}$。
$\because$在$Rt\triangle KBR'$中，$BK^{2}+BR'^{2}=KR'^{2}$，
$\therefore BK^{2}+ER^{2}=KR^{2}$，即$2^{2}+4^{2}=KR^{2}$。
$\therefore KR = 2\sqrt{5}$。
九年级下册