《2026年王朝霞考点梳理时习卷九年级数学全一册人教版》

21. (9分)交警部门提醒市民,骑车出行必须严格遵守“一盔一带”的规定.某头盔经销商统计了某品牌头盔7月份到9月份的销售量,该品牌头盔7月份销售量为500个,9月份销售量为720个,且从7月份到9月份销售量的月增长率相同.
(1)求该品牌头盔销售量的月增长率.
(2)若该品牌头盔的进价为30元/个,经测算,当售价为40元/个时,月销售量为600个,若在此基础上每个头盔的售价上涨1元,则月销售量将减少10个.为使月销售利润达到10 000元,而且尽可能让顾客得到实惠,该品牌头盔的实际售价应定为多少?

答案： 解：
(1)设该品牌头盔销售量的月增长率为x。
根据题意，得500(1 + x)² = 720。(2分)
解得x₁ = 0.2 = 20%，x₂ = −2.2(不合题意，舍去)。
答：该品牌头盔销售量的月增长率为20%。(4分)
(2)设该品牌头盔的实际售价应定为y元/个。
根据题意，得(y−30)[600−10(y−40)] = 10000。
整理，得y²−130y + 4000 = 0。(7分)
解得y₁ = 80(不合题意，舍去)，y₂ = 50。
答：该品牌头盔的实际售价应定为50元/个。(9分)

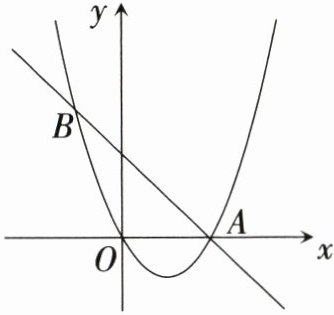
22.〔河南中考〕(10分)如图,抛物线$y = x^2 + mx$与直线$y = -x + b$交于点$A(2,0)$和点$B$.
(1)求$m$和$b$的值;
(2)求点$B$的坐标,并结合图象写出关于$x$的不等式$x^2 + mx ＞ -x + b$的解集;
(3)点$M$是直线$AB$上的一个动点,将点$M$向左平移3个单位长度得到点$N$,若线段$MN$与抛物线只有一个公共点,直接写出点$M$的横坐标$x_M$的取值范围.

答案：
解：
(1)
∵抛物线y = x² + mx经过点A(2，0)，
∴4 + 2m = 0，
∴m = −2。(2分)
∵直线y = −x + b经过点A(2，0)，
∴−2 + b = 0，
∴b = 2。(4分)
(2)当x²−2x = −x + 2时，解得x₁ = −1，x₂ = 2。
当x = −1时，y = −(−1) + 2 = 3。
∴点B的坐标为(−1，3)。(6分)
结合图象可知，关于x的不等式x² + mx＞−x + b的解集为x＜−1或x＞2。(8分)
(3)−1 ≤ xM＜2或xM = 3。(10分)
[解析]由
(1)知抛物线的解析式为y = x²−2x = (x−1)²−1，
∴抛物线的顶点坐标为(1，−1)。
∵点M是直线AB上的一个动点，将点M向左平移3个单位长度得到点N，
∴MN//x轴。
∵直线AB的解析式为y = −x + 2，
∴点N的轨迹为y = −(x + 3) + 2 = −x−1。
将点N的运动轨迹在同一平面直角坐标系表示出来如图所示。
　　　　　
由图象知分两种情况：①当点M在线段AB(不含点A)上运动时，线段MN与抛物线只有一个公共点，
∴−1 ≤ xM＜2。
②当线段MN经过抛物线的顶点(1，−1)时，线段MN与抛物线只有一个公共点。
∵MN//x轴，
∴点M的纵坐标为−1。
∴−xM + 2 = −1，
∴xM = 3。
综上所述，当线段MN与抛物线只有一个公共点时，−1 ≤ xM＜2或xM = 3。