2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
22. 设题新角度 过程性学习 (10分)模具厂计划生产面积为4,周长为$m$的矩形模具.对于$m$的取
值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)建立函数模型
设矩形相邻两边的长分别为$x,y$.由矩形的面积为4,得$xy=4$,即$y=\frac{4}{x}$;由周长为$m$,得
$2(x+y)=m$,即$y=-x+\frac{m}{2}$.满足要求的$(x,y)$应是两个函数图象在第
坐标.
(2)画出函数图象
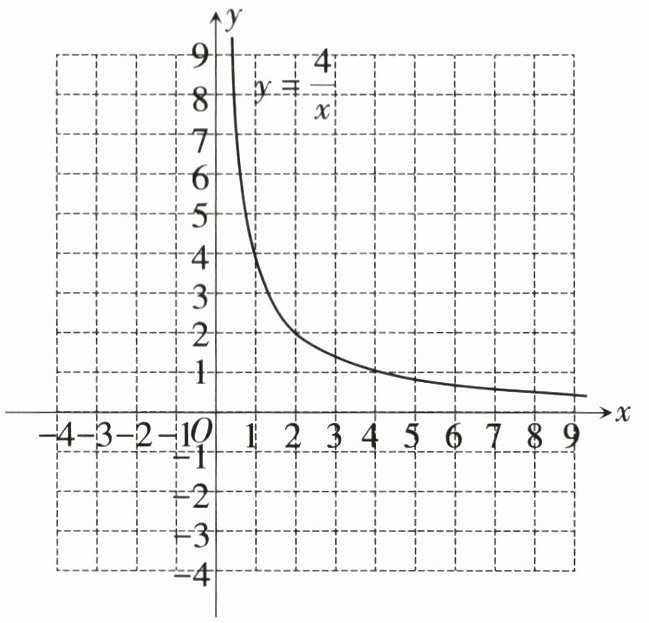
函数$y=\frac{4}{x} (x>0)$的图象如图所示,而函数$y=-x+\frac{m}{2}$的
图象可由直线$y=-x$平移得到,请在同一平面直角坐标系中直接画出直线$y=-x$.
(3)平移直线$y=-x$,观察函数图象
①当直线平移到与函数$y=\frac{4}{x} (x>0)$的图象有唯一交点
$(2,2)$时,周长$m$的值为
②在直线平移过程中,交点个数还有哪些情况?请直接写出交点个数及对应的周长$m$的取值
范围.
(4)得出结论
若能生产出面积为4的矩形模具,则周长$m$的取值范围为
值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)建立函数模型
设矩形相邻两边的长分别为$x,y$.由矩形的面积为4,得$xy=4$,即$y=\frac{4}{x}$;由周长为$m$,得
$2(x+y)=m$,即$y=-x+\frac{m}{2}$.满足要求的$(x,y)$应是两个函数图象在第
一
象限内交点的
坐标.
(2)画出函数图象
函数$y=\frac{4}{x} (x>0)$的图象如图所示,而函数$y=-x+\frac{m}{2}$的
图象可由直线$y=-x$平移得到,请在同一平面直角坐标系中直接画出直线$y=-x$.
(3)平移直线$y=-x$,观察函数图象
①当直线平移到与函数$y=\frac{4}{x} (x>0)$的图象有唯一交点
$(2,2)$时,周长$m$的值为
8
.②在直线平移过程中,交点个数还有哪些情况?请直接写出交点个数及对应的周长$m$的取值
范围.
(4)得出结论
若能生产出面积为4的矩形模具,则周长$m$的取值范围为
m≥8
.
答案:
解:
(1)一
(2)如图所示.

(3)①$8$
②直线与函数$y = \frac { 4 } { x } ( x > 0 )$的图象交点还有两种情况:当有$0$个交点时,周长$m$的取值范围是$0 < m < 8$;当有$2$个交点时,周长$m$的取值范围是$m > 8$.
(4)$m \geq 8$
解:
(1)一
(2)如图所示.

(3)①$8$
②直线与函数$y = \frac { 4 } { x } ( x > 0 )$的图象交点还有两种情况:当有$0$个交点时,周长$m$的取值范围是$0 < m < 8$;当有$2$个交点时,周长$m$的取值范围是$m > 8$.
(4)$m \geq 8$
23. [徐州模拟] (11分)如图,一次函数$y=kx+b$的图象与反比例函数$y=\frac{m}{x} (x>0)$的图象交于点
$A$,与$x$轴交于点$B(10,0)$.若$OB=AB$,且$S_{\triangle OAB}=30$.
(1)求反比例函数与一次函数的解析式;
(2)若$P$为$x$轴上一点,$\triangle ABP$是等腰三角形,求点$P$的坐标.
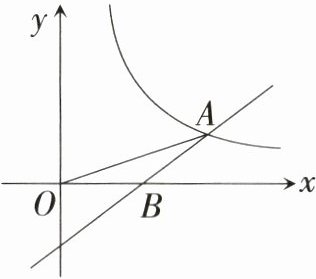
$A$,与$x$轴交于点$B(10,0)$.若$OB=AB$,且$S_{\triangle OAB}=30$.
(1)求反比例函数与一次函数的解析式;
(2)若$P$为$x$轴上一点,$\triangle ABP$是等腰三角形,求点$P$的坐标.

答案:
解:
(1)如图,过点$A$作$A D \perp x$轴于点$D$.
$\because$点$B$的坐标为$( 1 0 , 0 )$,$\therefore O B = 1 0$.
$\because S _ { \triangle O A B } = 3 0$,$\therefore \frac { 1 } { 2 } × 1 0 A D = 3 0$.$\therefore A D = 6$.
$\because O B = A B$,$\therefore A B = 1 0$.
在$ Rt \triangle A D B$中,由勾股定理,得$B D = \sqrt { A B ^ { 2 } - A D ^ { 2 } } = 8$.
$\therefore O D = O B + B D = 1 8$.
$\therefore$点$A$的坐标为$( 1 8 , 6 )$.
把点$A ( 1 8 , 6 )$代入$y = \frac { m } { x } ( x > 0 )$,得$m = 1 0 8$.
$\therefore$反比例函数的解析式为$y = \frac { 1 0 8 } { x } ( x > 0 )$.
把点$A ( 1 8 , 6 )$,$B ( 1 0 , 0 )$代入一次函数$y = k x + b$,
得$\begin{cases} 1 8 k + b = 6 , \\ 1 0 k + b = 0 . \end{cases}$解得$\begin{cases} k = \frac { 3 } { 4 } , \\ b = - \frac { 1 5 } { 2 } . \end{cases}$
$\therefore$一次函数的解析式为$y = \frac { 3 } { 4 } x - \frac { 1 5 } { 2 }$.

(2)当$\triangle A B P$是等腰三角形时,分三种情况:
①当$A B = P B$时,$P B = A B = 1 0$.
$\therefore$点$P$的坐标为$( 0 , 0 )$或$( 2 0 , 0 )$.
②当$A B = A P$时,如图.
$\because A D \perp x$轴,$\therefore D P = B D = 8$.
$\therefore O P = O B + B D + D P = 2 6$.
$\therefore$点$P$的坐标为$( 2 6 , 0 )$.
③当$P B = A P$时,点$P$在线段$A B$的垂直平分线与$x$轴的交点上.设点$P$的坐标为$( a , 0 )$,则$A P ^ { 2 } = P D ^ { 2 } + A D ^ { 2 } = ( 1 8 - a ) ^ { 2 } + 3 6$,$P B ^ { 2 } = ( a - 1 0 ) ^ { 2 }$.
$\therefore ( 1 8 - a ) ^ { 2 } + 3 6 = ( a - 1 0 ) ^ { 2 }$.解得$a = \frac { 6 5 } { 4 }$.
$\therefore$点$P$的坐标为$ ( \frac { 6 5 } { 4 } , 0 )$.
综上所述,当$\triangle A B P$是等腰三角形时,点$P$的坐标为$( 0 , 0 )$,$( 2 0 , 0 )$,$( 2 6 , 0 )$或$ ( \frac { 6 5 } { 4 } , 0 )$.
解:
(1)如图,过点$A$作$A D \perp x$轴于点$D$.
$\because$点$B$的坐标为$( 1 0 , 0 )$,$\therefore O B = 1 0$.
$\because S _ { \triangle O A B } = 3 0$,$\therefore \frac { 1 } { 2 } × 1 0 A D = 3 0$.$\therefore A D = 6$.
$\because O B = A B$,$\therefore A B = 1 0$.
在$ Rt \triangle A D B$中,由勾股定理,得$B D = \sqrt { A B ^ { 2 } - A D ^ { 2 } } = 8$.
$\therefore O D = O B + B D = 1 8$.
$\therefore$点$A$的坐标为$( 1 8 , 6 )$.
把点$A ( 1 8 , 6 )$代入$y = \frac { m } { x } ( x > 0 )$,得$m = 1 0 8$.
$\therefore$反比例函数的解析式为$y = \frac { 1 0 8 } { x } ( x > 0 )$.
把点$A ( 1 8 , 6 )$,$B ( 1 0 , 0 )$代入一次函数$y = k x + b$,
得$\begin{cases} 1 8 k + b = 6 , \\ 1 0 k + b = 0 . \end{cases}$解得$\begin{cases} k = \frac { 3 } { 4 } , \\ b = - \frac { 1 5 } { 2 } . \end{cases}$
$\therefore$一次函数的解析式为$y = \frac { 3 } { 4 } x - \frac { 1 5 } { 2 }$.

(2)当$\triangle A B P$是等腰三角形时,分三种情况:
①当$A B = P B$时,$P B = A B = 1 0$.
$\therefore$点$P$的坐标为$( 0 , 0 )$或$( 2 0 , 0 )$.
②当$A B = A P$时,如图.
$\because A D \perp x$轴,$\therefore D P = B D = 8$.
$\therefore O P = O B + B D + D P = 2 6$.
$\therefore$点$P$的坐标为$( 2 6 , 0 )$.
③当$P B = A P$时,点$P$在线段$A B$的垂直平分线与$x$轴的交点上.设点$P$的坐标为$( a , 0 )$,则$A P ^ { 2 } = P D ^ { 2 } + A D ^ { 2 } = ( 1 8 - a ) ^ { 2 } + 3 6$,$P B ^ { 2 } = ( a - 1 0 ) ^ { 2 }$.
$\therefore ( 1 8 - a ) ^ { 2 } + 3 6 = ( a - 1 0 ) ^ { 2 }$.解得$a = \frac { 6 5 } { 4 }$.
$\therefore$点$P$的坐标为$ ( \frac { 6 5 } { 4 } , 0 )$.
综上所述,当$\triangle A B P$是等腰三角形时,点$P$的坐标为$( 0 , 0 )$,$( 2 0 , 0 )$,$( 2 6 , 0 )$或$ ( \frac { 6 5 } { 4 } , 0 )$.
查看更多完整答案,请扫码查看


