2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
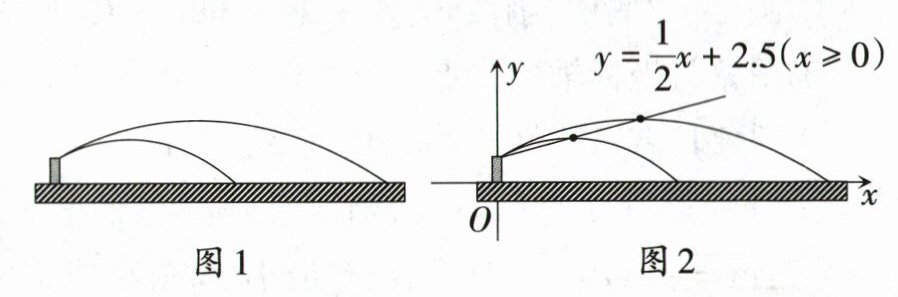
21. 〔洛阳市〕(9分)在一次学校组织的社会实践活动中,小洛看到农田里安装了很多灌溉喷枪,喷枪喷出的水流轨迹是抛物线(如图1),他发现这种喷枪射程是可调节的,且在一定的调节范围内喷射的水流越高射程越远,于是他从该农田的技术部门得到了这种喷枪的一组相关数据,通过研究发现,以地面为$x$轴,以喷枪所在直线为$y$轴,建立平面直角坐标系(如图2所示).设水流的最高点到地面的距离为$y( m)$,水流的最高点与喷枪的水平距离为$x( m)$,且满足$y=\frac{1}{2}x+2.5(x\geqslant0)$.
请解答下列问题:
(1) 该喷枪的出水口到地面的距离为
(2) 当水流的最高点与喷枪的水平距离为$7\ m$时,求水流的最高点到地面的距离;
(3) 在(2)的条件下,请计算水流的射程约为多少米(精确到1$ m$,参考数据$\sqrt{21}\approx4.58$).
请解答下列问题:
(1) 该喷枪的出水口到地面的距离为
2.5
$ m$;(2) 当水流的最高点与喷枪的水平距离为$7\ m$时,求水流的最高点到地面的距离;
(3) 在(2)的条件下,请计算水流的射程约为多少米(精确到1$ m$,参考数据$\sqrt{21}\approx4.58$).

答案:
21.解:
(1)$2.5$(2分)
(2)把$x = 7$代入$y=\frac{1}{2}x + 2.5$。
得$y=\frac{1}{2}×7 + 2.5 = 6$。
$\therefore$水流的最高点到地面的距离为$6m$。(5分)
(3)设水流的轨迹为$w=a(x - 7)^{2}+6$。
把$(0,2.5)$代入,得$a=-\frac{1}{14}$。
$\therefore w=-\frac{1}{14}(x - 7)^{2}+6$。(7分)
当$w = 0$时,$-\frac{1}{14}(x - 7)^{2}+6 = 0$。
解得$x_{1}=7 + 2\sqrt{21}$,$x_{2}=7 - 2\sqrt{21}$(舍去)。
$\therefore$水流的射程约为$7 + 2\sqrt{21}\approx7 + 2×4.58 = 16.16\approx16(m)$。(9分)
(1)$2.5$(2分)
(2)把$x = 7$代入$y=\frac{1}{2}x + 2.5$。
得$y=\frac{1}{2}×7 + 2.5 = 6$。
$\therefore$水流的最高点到地面的距离为$6m$。(5分)
(3)设水流的轨迹为$w=a(x - 7)^{2}+6$。
把$(0,2.5)$代入,得$a=-\frac{1}{14}$。
$\therefore w=-\frac{1}{14}(x - 7)^{2}+6$。(7分)
当$w = 0$时,$-\frac{1}{14}(x - 7)^{2}+6 = 0$。
解得$x_{1}=7 + 2\sqrt{21}$,$x_{2}=7 - 2\sqrt{21}$(舍去)。
$\therefore$水流的射程约为$7 + 2\sqrt{21}\approx7 + 2×4.58 = 16.16\approx16(m)$。(9分)
22. 设题新角度 过程性学习 (10分)函数图象是研究函数的重要工具,结合已有的学习函数图象和性质的经验,请画出函数$y=x(x-3)^2(x\geqslant0)$的图象,探究该函数的性质并解答问题.
(1) 绘制函数图象.
① 列表:下表是$x$与$y$的几组对应值,其中$a=$

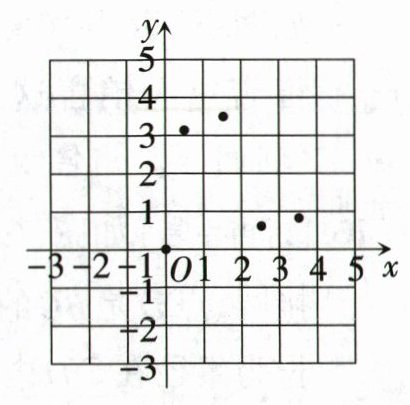
② 描点连线:请在如图的平面直角坐标系中将表中未描出的点补充完整,并用平滑的曲线依次连接.
(2) 探究函数性质.
请写出函数$y=x(x-3)^2(x\geqslant0)$的两条性质:
①
(3) 结合(1)(2)的分析,解决问题.
① 若关于$x$的方程$x(x-3)^2=k(x\geqslant0)$有三个不相等的实数根,则$k$的取值范围是
② 若关于$x$的方程$x(x-3)^2=mx-1(x\geqslant0)$有一个实数根为2,则该方程其他的实数根约为
(1) 绘制函数图象.
① 列表:下表是$x$与$y$的几组对应值,其中$a=$
4
;
② 描点连线:请在如图的平面直角坐标系中将表中未描出的点补充完整,并用平滑的曲线依次连接.
(2) 探究函数性质.
请写出函数$y=x(x-3)^2(x\geqslant0)$的两条性质:

①
当x=0或x=3时,y有最小值0
;② 当$0\leq x\leq1$时,y随x的增大而增大
.(3) 结合(1)(2)的分析,解决问题.
① 若关于$x$的方程$x(x-3)^2=k(x\geqslant0)$有三个不相等的实数根,则$k$的取值范围是
$0\lt k\lt4$
;② 若关于$x$的方程$x(x-3)^2=mx-1(x\geqslant0)$有一个实数根为2,则该方程其他的实数根约为
4.1
(结果保留小数点后一位).
答案:
22.解:
(1)①$4$(1分)
②所补充的点,所画曲线如图所示。

(4分)
(2)①当$x = 0$或$x = 3$时,$y$有最小值$0$
②当$0\leq x\leq1$时,$y$随$x$的增大而增大
(①,②答案不唯一)(6分)
(3)①$0\lt k\lt4$
②$4.1$(答案合理即可)(10分)
22.解:
(1)①$4$(1分)
②所补充的点,所画曲线如图所示。

(4分)
(2)①当$x = 0$或$x = 3$时,$y$有最小值$0$
②当$0\leq x\leq1$时,$y$随$x$的增大而增大
(①,②答案不唯一)(6分)
(3)①$0\lt k\lt4$
②$4.1$(答案合理即可)(10分)
查看更多完整答案,请扫码查看


