《2025年百年学典快乐假期暑假作业七年级人教版》

10. 已知$∠α=45.15^{\circ }$，将$∠α$表示为度、分、秒的形式为$45 ^ { \circ } 9 ^ { \prime }$；$18^{\circ }45'36''$用度表示为18.76$^{\circ }$.

答案： $45 ^ { \circ } 9 ^ { \prime }$ 18.76

11. 计算：$51^{\circ }32'+16^{\circ }28'=$$68^{\circ }$；
$90^{\circ }-42^{\circ }28'10''=$47$^{\circ }$31$'$50$''$；
$30^{\circ }21'×4=$$121^{\circ }24'$.

答案： $68 ^ { \circ }$ 47 31 50 $121 ^ { \circ } 24 ^ { \prime }$

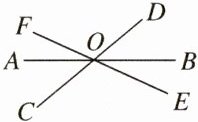
12. 如下图所示，直线$AB$，$CD$，$EF$相交于点$O$，则$∠AOD$的对顶角是$ \angle B O C $，$∠AOC$的邻补角是$ \angle A O D $ 和 $ \angle C O B $；若$∠AOC=50^{\circ }$，则$∠BOD=$$ 50 ^ { \circ } $，$∠COB=$$ 130 ^ { \circ } $.

答案： $ \angle B O C $ $ \angle A O D $ 和 $ \angle C O B $ $ 50 ^ { \circ } $ $ 130 ^ { \circ } $

13. 若$∠α$与$∠β$是对顶角，$∠α$的补角是$110^{\circ }$，则$∠β$的余角的度数为$20^{\circ }$.

答案： $ 20 ^ { \circ } $

14. 如下图所示，$P$是直线$l$外一点，$A$，$B$，$C$是直线$l$上的三点，且$PB$与$l$垂直，在从点$P$到直线$l$的多条道路中，最短路线是④（填序号），理由是垂线段最短.

答案： ④ 垂线段最短

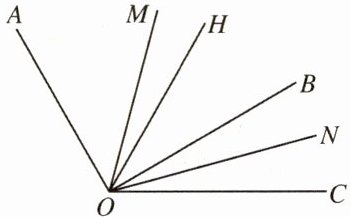
15. 如下图所示，过点$O$在$∠AOC$内部作射线$OB$，且$OH$平分$∠AOC$，$OM$平分$∠AOB$，$ON$平分$∠BOC$. 有下列结论：
①$∠MON=∠HOC$；
②$∠MON=\frac {∠AOC+∠BOH}{2}$；
③$∠MOH=\frac {∠AOH-∠BOH}{2}$；
④$∠HOC+∠HOB=2∠HON$.
其中正确的是____①③④（填序号）.

答案： ①③④

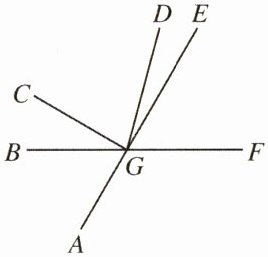
16. 如下图所示，直线$AE$，$BF$相交于点$G$，$GC⊥GE$，$GD$平分$∠CGF$，若$∠DGE:∠EGF=1:4$，则$∠BGC=$$30^{\circ}$.

答案： $ 30 ^ { \circ } $

17. 如右下图所示，直线$AB$，$CD$相交于点$O$，$OM⊥AB$.
（1）若$∠1=40^{\circ }$，$∠2=30^{\circ }$，求$∠NOD$的度数；$100^{\circ }$
（2）如果$∠1=∠2$，那么$ON$与$CD$互相垂直吗？请说明理由.垂直
$\because \angle 1 + \angle A O C = 90 ^ { \circ }, \angle 1 = \angle 2 $,$\therefore \angle 2 + \angle A O C = 90 ^ { \circ } $, 即 $ \angle C O N = 90 ^ { \circ } $,$\therefore O N \perp C D $.

答案： 解:
(1) $ \angle N O D = \angle D O C - \angle A O C - \angle 2 = 100 ^ { \circ } $.
(2) $ O N \perp C D $.
$ \because \angle 1 + \angle A O C = 90 ^ { \circ }, \angle 1 = \angle 2 $,
$ \therefore \angle 2 + \angle A O C = 90 ^ { \circ } $, 即 $ \angle C O N = 90 ^ { \circ } $,
$ \therefore O N \perp C D $.

18. 如右下图所示，直线$a$，$b$相交.
（1）若$∠1=40^{\circ }$，求$∠2$，$∠3$，$∠4$的度数；$∠2=$$140^{\circ }$，$∠3=$$40^{\circ }$，$∠4=$$140^{\circ }$
（2）若$∠1:∠2=2:7$，求各角的度数.$∠1=∠3=$$40^{\circ }$，$∠2=∠4=$$140^{\circ }$

答案： 解:
(1) $ \angle 2 = \angle 4 = 140 ^ { \circ }, \angle 3 = 40 ^ { \circ } $.
(2) $ \angle 1 = \angle 3 = 40 ^ { \circ }, \angle 2 = \angle 4 = 140 ^ { \circ } $.