《2025年百年学典快乐假期暑假作业七年级人教版》

16. 安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害，为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动. 在活动前和活动后分别随机抽取了部分使用电瓶车的市民，就骑电瓶车戴安全帽情况进行问卷调查，将收集的数据制成如下统计图表.

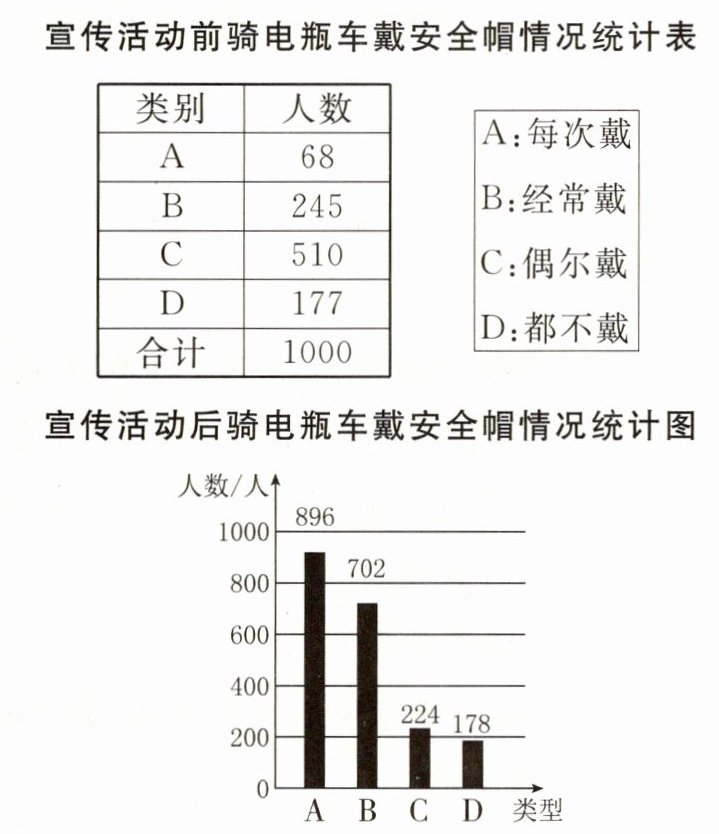
（1）宣传活动前，在抽取的市民中偶尔戴类别的人数最多？占抽取人数的百分之几？51%
（2）该市约有 30 万人使用电瓶车，请估计宣传活动前全市骑电瓶车“都不戴”安全帽的总人数.5.31万人
（3）小明认为，宣传活动后全市骑电瓶车“都不戴”安全帽的人数为 178，比宣传活动前增加了 1 人，因此交警部门开展的宣传活动没有效果. 小明分析数据的方法是否合理？不合理请结合统计图表，谈谈你对小明分析数据的方法及交警部门宣传活动的效果的看法.宣传活动后全市骑电瓶车“都不戴”安全帽的百分比为8.9%，宣传活动前为17.7%，8.9%＜17.7%，所以交警部门开展的宣传活动有效果。

答案： 解：
(1) 宣传活动前，在抽取的市民中“偶尔戴”的人数最多，占抽取人数的 $\frac{510}{1000} \times 100\% = 51\%$。
(2) 估计宣传活动前全市骑电瓶车“都不戴”安全帽的总人数约为 $30 \times \frac{177}{1000} = 5.31$（万人）。
(3) 小明分析数据的方法不合理，理由如下：
宣传活动后全市骑电瓶车“都不戴”安全帽的百分比为 $\frac{178}{896 + 702 + 224 + 178} \times 100\% = 8.9\%$。
宣传活动前全市骑电瓶车“都不戴”安全帽的百分比为 $\frac{177}{1000} \times 100\% = 17.7\%$。
$\because 8.9\% ＜ 17.7\%$，
$\therefore$ 小明分析数据的方法不合理，交警部门开展的宣传活动有效果。

17. 某园林的门票每张 $ 10 $ 元，只能使用一次. 考虑到人们的不同需求，也为了吸引更多游客，该园林除保留原来的售票方法外，还推出了一种“购买个人年票”的售票方法（个人年票从购买日起，可供持票者使用一年）. 年票分 $ \mathrm { A } $，$ \mathrm { B } $，$ \mathrm { C } $ 三类：$ \mathrm { A } $ 类年票每张 $ 120 $ 元，持票者进入园林时，无须再买门票；$ \mathrm { B } $ 类年票每张 $ 60 $ 元，持票者进入该园林时，须再购买门票，每次 $ 2 $ 元；$ \mathrm { C } $ 类年票每张 $ 40 $ 元，持票者进入该园林时，须再购买门票，每次 $ 3 $ 元.
（1）如果你只选择一种购买门票的方式，并且你计划在一年中用 $ 80 $ 元花在该园林的门票上，试通过计算，找出可使进入该园林的次数最多的购票方式；
（2）一年中进入该园林至少超过多少次时，购买 $ \mathrm { A } $ 类年票比较合算？

答案： 解：
(1) $\because 80 ＜ 120$，$\therefore$ 不可能选 A 类年票。
若选 B 类年票，则能进入 $\frac{80 - 60}{2} = 10$（次）；
若选 C 类年票，则能进入 $\frac{80 - 40}{3} \approx 13$（次）；
若不购买年票，则能进入 $\frac{80}{10} = 8$（次）。
所以计划用 80 元花在该园林的门票上时，选择购买 C 类年票的方法进入园林的次数最多，为 13 次。
(2) 设至少超过 $x$ 次时，购买 A 类年票比较合算，
则有不等式组 $\begin{cases}60 + 2x ＞ 120, \\ 40 + 3x ＞ 120, \\ 10x ＞ 120.\end{cases}$ 解得 $\begin{cases}x ＞ 30, \\ x ＞ \frac{80}{3}, \\ x ＞ 12.\end{cases}$
$\therefore x ＞ 30$，$\therefore$ 一年中进入该园林至少超过 30 次时，购买 A 类年票比较合算。