第130页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
1. 若关于 $ x $ 的方程 $ x - 2 + 3k = \frac { x + k } { 3 } $ 的根是负数,则 $ k $ 的取值范围是(
A. $ k > \frac { 3 } { 4 } $
B. $ k \geq \frac { 3 } { 4 } $
C. $ k < \frac { 3 } { 4 } $
D. $ k \leq \frac { 3 } { 4 } $
A
)A. $ k > \frac { 3 } { 4 } $
B. $ k \geq \frac { 3 } { 4 } $
C. $ k < \frac { 3 } { 4 } $
D. $ k \leq \frac { 3 } { 4 } $
答案:
A
2. 在方程组 $ \left\{ \begin{array} { l } { 2 x + y = 1 - m, } \\ { x + 2 y = 2 } \end{array} \right. $ 中,若未知数 $ x $,$ y $ 满足 $ x + y > 0 $,则 $ m $ 的取值范围在数轴上表示应该是(

B
)
答案:
B
3. 两人练习跑步,如果乙先跑 $ 16 \mathrm { m } $,则甲 $ 8 \mathrm { s } $ 可追上乙;如果乙先跑 $ 2 \mathrm { s } $,则甲 $ 4 \mathrm { s } $ 可追上乙. 甲、乙二人每秒各跑多少米?若设甲每秒跑 $ x \mathrm { m } $,乙每秒跑 $ y \mathrm { m } $,则所列方程组应该是(
A. $ \left\{ \begin{array} { l } { 16 = 8 ( x - y ), } \\ { ( 2 + 4 ) y = 4 x } \end{array} \right. $
B. $ \left\{ \begin{array} { l } { 8 x - 8 y = 16, } \\ { 4 x - 4 y = 4 } \end{array} \right. $
C. $ \left\{ \begin{array} { l } { 8 x - 16 = 5 y, } \\ { 4 x - 4 y = 2 } \end{array} \right. $
D. $ \left\{ \begin{array} { l } { 8 x = 8 y + 16, } \\ { 4 x - 2 = 4 y } \end{array} \right. $
A
)A. $ \left\{ \begin{array} { l } { 16 = 8 ( x - y ), } \\ { ( 2 + 4 ) y = 4 x } \end{array} \right. $
B. $ \left\{ \begin{array} { l } { 8 x - 8 y = 16, } \\ { 4 x - 4 y = 4 } \end{array} \right. $
C. $ \left\{ \begin{array} { l } { 8 x - 16 = 5 y, } \\ { 4 x - 4 y = 2 } \end{array} \right. $
D. $ \left\{ \begin{array} { l } { 8 x = 8 y + 16, } \\ { 4 x - 2 = 4 y } \end{array} \right. $
答案:
A
4. 按照如下图所示的操作步骤,若输入的值是 $ \sqrt [ 3 ] { 27 } $,则输出的值为(
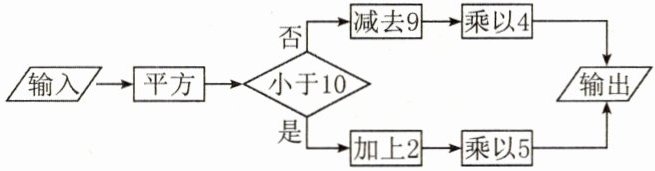
A. $ 45 $
B. $ 50 $
C. $ 55 $
D. $ 66 $
C
)
A. $ 45 $
B. $ 50 $
C. $ 55 $
D. $ 66 $
答案:
C
5. 某商贩去买黄瓜,他先买了 $ 30 $ 斤,价格为每斤 $ x $ 元;接着,他又买了 $ 20 $ 斤,价格为每斤 $ y $ 元. 当他以每斤 $ \frac { x + y } { 2 } $ 元的售价卖完后,结果发现自己赔了钱,其原因是(
A. $ x < y $
B. $ x > y $
C. $ x \leq y $
D. $ x \geq y $
B
)A. $ x < y $
B. $ x > y $
C. $ x \leq y $
D. $ x \geq y $
答案:
B
6. 如右图所示,在平面直角坐标系中,$ A ( 1,1 ) $,$ B ( - 1,1 ) $,$ C ( - 1, - 2 ) $,$ D ( 1, - 2 ) $. 把一条长为 $ 2025 $ 个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点 $ A $ 处,并按 $ A - B - C - D - A - \cdots $ 的规律紧绕在四边形 $ A B C D $ 的边上,则细线另一端所在位置的点的坐标是(
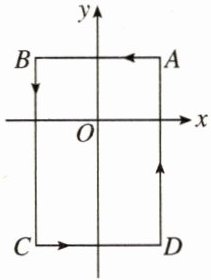
A. $ ( 1, - 1 ) $
B. $ ( - 1,1 ) $
C. $ ( - 1, - 2 ) $
D. $ ( 1, - 2 ) $
C
)
A. $ ( 1, - 1 ) $
B. $ ( - 1,1 ) $
C. $ ( - 1, - 2 ) $
D. $ ( 1, - 2 ) $
答案:
C
7. 我们称使方程 $ \frac { x } { 2 } + \frac { y } { 3 } = \frac { x + y } { 2 + 3 } $ 成立的一对数 $ x $,$ y $ 为“相伴数对”,记为 $ ( x, y ) $.
(1)若 $ ( 6, y ) $ 是“相伴数对”,则 $ y $ 的值为
(2)若 $ ( a, b ) $ 是“相伴数对”,则 $ b = $
(1)若 $ ( 6, y ) $ 是“相伴数对”,则 $ y $ 的值为
$-\frac{27}{2}$
;(2)若 $ ( a, b ) $ 是“相伴数对”,则 $ b = $
$-\frac{9}{4}a$
(用含 $ a $ 的代数式表示).
答案:
(1) $-\frac{27}{2}$
(2) $-\frac{9}{4}a$
(1) $-\frac{27}{2}$
(2) $-\frac{9}{4}a$
8. 如下图所示,已知 $ \angle 1 = \angle 2 $,$ \angle A = 72 ^ { \circ } $,则 $ \angle A D C = $______
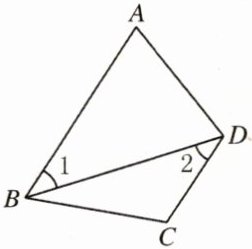
$108^{\circ}$
.
答案:
$108^{\circ}$
9. 有人问一位老师所教班级有多少名学生,老师说:“一半学生在做数学,四分之一的学生在画画,七分之一的学生在读英语,还剩不足七名同学在操场上玩.”那么这个班最多有学生
56
名.
答案:
56
查看更多完整答案,请扫码查看


