第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
1. 科学计数法
把1000记为
把1000记为
$1 × 10^{3}$
,把10000记为$1 × 10^{4}$
,把0.001记为$1 × 10^{-3}$
,把0.01记为$1 × 10^{-2}$
。
答案:
【解析】:
本题考查科学记数法的表示方法。
科学记数法是一种表示大数或小数的方法,其形式为 $a × 10^{n}$,其中 $1 \leq a < 10$ 且 $n$ 为整数。
对于 $1000$,可以表示为 $1 × 10^{3}$;
对于 $10000$,可以表示为 $1 × 10^{4}$;
对于 $0.001$,可以表示为 $1 × 10^{-3}$;
对于 $0.01$,可以表示为 $1 × 10^{-2}$。
【答案】:
$1 × 10^{3}$;$1 × 10^{4}$;$1 × 10^{-3}$;$1 × 10^{-2}$。
本题考查科学记数法的表示方法。
科学记数法是一种表示大数或小数的方法,其形式为 $a × 10^{n}$,其中 $1 \leq a < 10$ 且 $n$ 为整数。
对于 $1000$,可以表示为 $1 × 10^{3}$;
对于 $10000$,可以表示为 $1 × 10^{4}$;
对于 $0.001$,可以表示为 $1 × 10^{-3}$;
对于 $0.01$,可以表示为 $1 × 10^{-2}$。
【答案】:
$1 × 10^{3}$;$1 × 10^{4}$;$1 × 10^{-3}$;$1 × 10^{-2}$。
2. 长度单位
(1)在国际单位制中,长度的基本单位是
(2)单位换算:
1km=
1cm=
1μm=
(1)在国际单位制中,长度的基本单位是
米
,符号是m
。常用的长度单位还有千米
、分米
、厘米
、毫米
、微米
、纳米
等。(2)单位换算:
1km=
1000
m 1dm=0.1
m1cm=
0.01
m 1mm=0.001
m1μm=
10⁻⁶
m 1nm=10⁻⁹
m
答案:
(1)米;m;千米;分米;厘米;毫米;微米;纳米
(2)1000;0.1;0.01;0.001;10⁻⁶;10⁻⁹
(1)米;m;千米;分米;厘米;毫米;微米;纳米
(2)1000;0.1;0.01;0.001;10⁻⁶;10⁻⁹
3. 测量长度
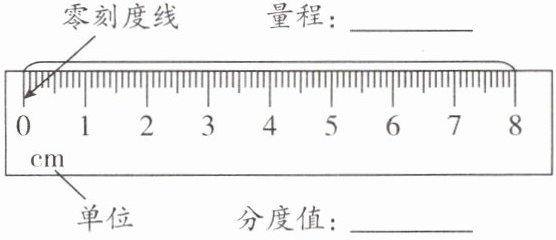
(1)认识刻度尺:
常用的长度测量工具——刻度尺(如图)。
(2)测量方法:
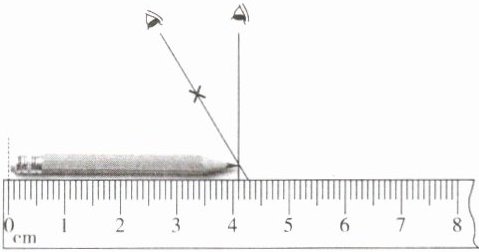
如图所示,测量时,物体的一端与____对齐。读数时,视线应____刻度线,估读到最小刻度值的____位。
(3)测量结果:
测量结果是由____和____构成的。数字又分____值和____值。如果某次测量结果是31.4mm,则31.4是测量结果的____部分,mm是测量结果的____部分;31是____值,4是____值。
(1)认识刻度尺:
常用的长度测量工具——刻度尺(如图)。

(2)测量方法:

如图所示,测量时,物体的一端与____对齐。读数时,视线应____刻度线,估读到最小刻度值的____位。
(3)测量结果:
测量结果是由____和____构成的。数字又分____值和____值。如果某次测量结果是31.4mm,则31.4是测量结果的____部分,mm是测量结果的____部分;31是____值,4是____值。
答案:
【例1】 3200=
$3.2 × 10^{3}$
;0.0067=$6.7 × 10^{-3}$
。
答案:
【解析】:
这道题目考察的是科学记数法的运用,即如何将一个数表示为$a × 10^{n}$的形式,其中$1 \leq a < 10$,n为整数。对于较大的数,我们需要将小数点向左移动,使得数值在1到10之间,同时记录移动了多少位来确定10的指数n。对于较小的数,我们需要将小数点向右移动,同样使得数值在1到10之间,并记录移动的位数以确定负的10的指数。
对于3200,我们可以将其表示为$3.2 × 1000 = 3.2 × 10^{3}$。
对于0.0067,我们可以将其表示为$6.7 × 0.001 = 6.7 × 10^{-3}$。
【答案】:
$3.2 × 10^{3}$;$6.7 × 10^{-3}$。
这道题目考察的是科学记数法的运用,即如何将一个数表示为$a × 10^{n}$的形式,其中$1 \leq a < 10$,n为整数。对于较大的数,我们需要将小数点向左移动,使得数值在1到10之间,同时记录移动了多少位来确定10的指数n。对于较小的数,我们需要将小数点向右移动,同样使得数值在1到10之间,并记录移动的位数以确定负的10的指数。
对于3200,我们可以将其表示为$3.2 × 1000 = 3.2 × 10^{3}$。
对于0.0067,我们可以将其表示为$6.7 × 0.001 = 6.7 × 10^{-3}$。
【答案】:
$3.2 × 10^{3}$;$6.7 × 10^{-3}$。
变式训练1 54300=
5.43 × 10^{4}
;0.0000123=1.23 × 10^{-5}
。
答案:
【解析】:
这道题目考查的是科学记数法的运用。科学记数法是一种表示大数或小数的方法,其形式为$a × 10^{n}$,其中$1 \leq a < 10$,$n$为整数。对于大数,$n$为正数,表示小数点向右移动的位数;对于小数,$n$为负数,其绝对值表示小数点向左移动的位数。
对于$54300$,我们可以将其表示为$5.43 × 10^{4}$,因为$54300$的小数点原本在最后,向左移动了4位到达$5.43$,所以$n=4$。
对于$0.0000123$,我们可以将其表示为$1.23 × 10^{-5}$,因为$0.0000123$的小数点需要向右移动5位才能变为$1.23$,所以$n=-5$。
【答案】:
$5.43 × 10^{4}$;$1.23 × 10^{-5}$
这道题目考查的是科学记数法的运用。科学记数法是一种表示大数或小数的方法,其形式为$a × 10^{n}$,其中$1 \leq a < 10$,$n$为整数。对于大数,$n$为正数,表示小数点向右移动的位数;对于小数,$n$为负数,其绝对值表示小数点向左移动的位数。
对于$54300$,我们可以将其表示为$5.43 × 10^{4}$,因为$54300$的小数点原本在最后,向左移动了4位到达$5.43$,所以$n=4$。
对于$0.0000123$,我们可以将其表示为$1.23 × 10^{-5}$,因为$0.0000123$的小数点需要向右移动5位才能变为$1.23$,所以$n=-5$。
【答案】:
$5.43 × 10^{4}$;$1.23 × 10^{-5}$
【例2】 我们现在使用的初中物理课本的宽度约为 (
A.18nm
B.18mm
C.18cm
D.18dm
C
)A.18nm
B.18mm
C.18cm
D.18dm
答案:
【解析】:
本题主要考查对生活中常见物体长度的估测能力。需要理解不同长度单位之间的换算关系,并能根据生活经验判断物体的实际长度。题目给出了四个选项,分别用不同的长度单位表示,要求我们选择出符合初中物理课本实际宽度的选项。
A选项,$18nm$,这个长度太小,几乎可以忽略不计,显然不符合课本的实际宽度。
B选项,$18mm$,这个长度也太小,相当于一个小物体的尺寸,同样不符合课本的实际宽度。
C选项,$18cm$,这个长度比较符合我们对初中物理课本宽度的实际认知。
D选项,$18dm$,这个长度太大,相当于一个比较大的物体的尺寸,不符合课本的实际宽度。
综上所述,我们可以确定C选项是最符合实际的答案。
【答案】:
C
本题主要考查对生活中常见物体长度的估测能力。需要理解不同长度单位之间的换算关系,并能根据生活经验判断物体的实际长度。题目给出了四个选项,分别用不同的长度单位表示,要求我们选择出符合初中物理课本实际宽度的选项。
A选项,$18nm$,这个长度太小,几乎可以忽略不计,显然不符合课本的实际宽度。
B选项,$18mm$,这个长度也太小,相当于一个小物体的尺寸,同样不符合课本的实际宽度。
C选项,$18cm$,这个长度比较符合我们对初中物理课本宽度的实际认知。
D选项,$18dm$,这个长度太大,相当于一个比较大的物体的尺寸,不符合课本的实际宽度。
综上所述,我们可以确定C选项是最符合实际的答案。
【答案】:
C
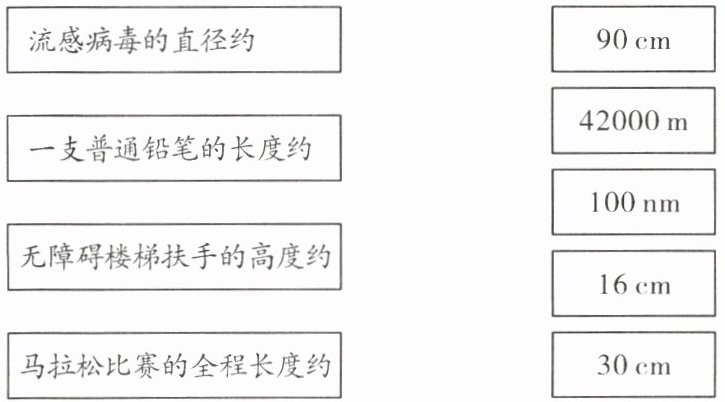
变式训练2 请用连线的方式将左侧的情景与右侧相应的选项连接起来。

答案:
【解析】:
本题考查对生活中常见物体长度的估测以及长度单位的换算能力。
流感病毒的直径非常小,通常用纳米($nm$)作为单位来衡量,$100nm$是比较合理的。
一支普通铅笔的长度一般在$15cm - 20cm$左右,$16cm$符合实际情况。
无障碍楼梯扶手的高度通常是为了方便人们扶握,一般在$0.9m$左右,因为$1m = 100cm$,所以$0.9m=90cm$。
马拉松比赛的全程长度是固定的,为$42.195km$,因为$1km = 1000m$,$42.195km\approx42000m$。
【答案】:
流感病毒的直径约------$100nm$;
一支普通铅笔的长度约------$16cm$;
无障碍楼梯扶手的高度约------$90cm$;
马拉松比赛的全程长度约------$42000m$。
本题考查对生活中常见物体长度的估测以及长度单位的换算能力。
流感病毒的直径非常小,通常用纳米($nm$)作为单位来衡量,$100nm$是比较合理的。
一支普通铅笔的长度一般在$15cm - 20cm$左右,$16cm$符合实际情况。
无障碍楼梯扶手的高度通常是为了方便人们扶握,一般在$0.9m$左右,因为$1m = 100cm$,所以$0.9m=90cm$。
马拉松比赛的全程长度是固定的,为$42.195km$,因为$1km = 1000m$,$42.195km\approx42000m$。
【答案】:
流感病毒的直径约------$100nm$;
一支普通铅笔的长度约------$16cm$;
无障碍楼梯扶手的高度约------$90cm$;
马拉松比赛的全程长度约------$42000m$。
【例3】 完成下列长度单位的换算。
(1)2.8m=
(2)3.5nm=
(1)2.8m=
2.8×10⁻³
km= 2.8×10²cm
。(2)3.5nm=
3.5×10⁻⁹
m= 3.5×10⁻³μm
。
答案:
(1)解:因为$1m = 10^{-3}km$,所以$2.8m=2.8×10^{-3}km$;因为$1m = 10^{2}cm$,所以$2.8m = 2.8×10^{2}cm$。
故答案依次为$2.8×10^{-3}$;$cm$。
(2)解:因为$1nm=10^{-9}m$,所以$3.5nm = 3.5×10^{-9}m$;因为$1nm = 10^{-3}\mu m$,所以$3.5nm=3.5×10^{-3}\mu m$。
故答案依次为$3.5×10^{-9}$;$\mu m$。
(1)解:因为$1m = 10^{-3}km$,所以$2.8m=2.8×10^{-3}km$;因为$1m = 10^{2}cm$,所以$2.8m = 2.8×10^{2}cm$。
故答案依次为$2.8×10^{-3}$;$cm$。
(2)解:因为$1nm=10^{-9}m$,所以$3.5nm = 3.5×10^{-9}m$;因为$1nm = 10^{-3}\mu m$,所以$3.5nm=3.5×10^{-3}\mu m$。
故答案依次为$3.5×10^{-9}$;$\mu m$。
查看更多完整答案,请扫码查看


