《2025年天府前沿八年级物理上册教科版课时同步培优训练》

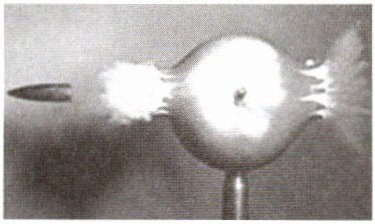
12. (新编)如图所示的是用高速摄影机拍摄子弹打穿苹果的画面。已知打穿苹果的时间为$3.0×10^{-4}s$,则子弹的速度约为(C)

A.50m/s
B.100m/s
C.200m/s
D.400m/s

答案： 解：估计苹果直径约为0.06m，子弹穿过苹果的路程s≈0.06m，时间t=3.0×10⁻⁴s。
根据速度公式v=s/t，可得v=0.06m/(3.0×10⁻⁴s)=200m/s。
答案：C

13. (新编)为了测定某辆轿车在平直公路上行驶的速度,小宇同学拍摄了在同一底片上多次曝光的照片,如图所示。如果每隔1s拍摄1次,轿车本身总长4.5m,那么这辆轿车2s内的速度约为(A)

A.9.5m/s
B.12.5m/s
C.15m/s
D.30m/s

答案： 解：由图可知，轿车在2s内通过的路程约为轿车车身长度的3倍多一点，轿车总长4.5m，故路程s≈4.5m×3.3≈15m，时间t=2s，速度v=s/t=15m/2s=7.5m/s，最接近选项A。
答案：A

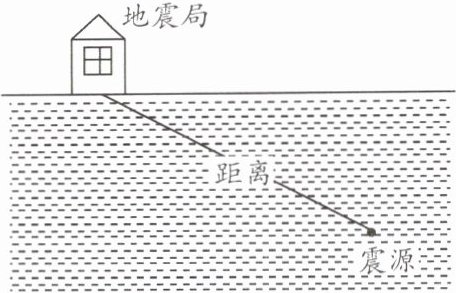
14. (常州中考)2021年12月22日,常州发生4.2级地震,震源处同时产生并向各个方向发出P波和S波。P波的传播速度是$7×10^{3}m/s$,S波的传播速度是$3.5×10^{3}m/s$,常州市地震局于当日21h46min07s探测到P波,于当日21h46min09s探测到S波。
(1)地震局距离震源有多远?
(2)求震源发生地震的时刻。

答案： 【解析】：
本题主要考查速度公式的应用以及如何通过已知信息计算距离和时间。
（1）首先，需要计算P波和S波到达地震局的时间差，然后利用这个时间差和两种波的速度差来计算地震局到震源的距离。
（2）利用已知的P波速度和传播时间来计算震源到地震局的距离所需的时间，然后从探测到P波的时间反推震源发生地震的时刻。
【答案】：
(1)解：由题意可得，地震局探测到P波、S波的时间间隔为：$\Delta t = 21h46min09s - 21h46min07s = 2s$，
设地震局到震源的距离为$s$，由于P波和S波从震源同时出发，传播到地震局的时间差为$\Delta t$，则有：
$t_{S} - t_{P} = \Delta t$，
根据速度公式$v = \frac{s}{t}$，可以得到P波和S波传播的时间分别为：
$t_{P} = \frac{s}{v_{P}}$，
$t_{S} = \frac{s}{v_{S}}$，
将上述两式代入时间差的等式中，得到：
$\frac{s}{v_{S}} - \frac{s}{v_{P}} = \Delta t$，
代入已知的P波和S波的速度，以及时间差，可以解出$s$：
$s = \frac{v_{S} × v_{P} × \Delta t}{v_{P} - v_{S}} = \frac{3.5 × 10^{3} × 7 × 10^{3} × 2}{7 × 10^{3} - 3.5 × 10^{3}} = 1.4 × 10^{4} \text{m} = 14 \text{km}$。
综上，地震局距离震源有14km。
(2)解：利用已知的P波速度和传播距离来计算P波从震源传播到地震局所需的时间：
$t_{P} = \frac{s}{v_{P}} = \frac{14 × 10^{3}}{7 × 10^{3}} = 2\text{s}$，
由于地震局探测到P波的时间是$21h46min07s$，所以震源发生地震的时刻为：
$21h46min07s - 2s = 21h46min05s$。
综上，震源发生地震的时刻为$21h46min05s$。

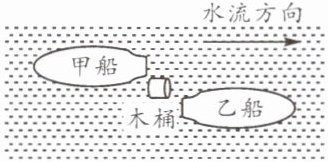
15. (金牛区期末)流速为5km/h的河流中有一只自由漂浮的木桶,甲、乙两船同时从木桶位置出发,均以相对水30km/h的速度分别逆流、顺流而行,1h后两船离木桶的距离是( )B

A.甲船25km,乙船35km
B.甲船30km,乙船30km
C.甲船35km,乙船30km
D.无法确定

答案： 【解析】：
本题主要考查了速度的计算以及运动学中的相对运动问题。需要理解在流水行船问题中，顺流速度、逆流速度、水流速度以及船在静水中的速度之间的关系，并据此计算出两船在1小时内离木桶的距离。
计算甲船离木桶的距离：
甲船逆流而行，其实际速度为船在静水中的速度减去水流速度，即 $v_{甲} = 30 - 5 = 25km/h$。
由于木桶是自由漂浮的，所以它的速度等于水流速度，即 $v_{桶} = 5km/h$。
甲船和木桶的相对速度为 $v_{甲桶} = v_{甲} + v_{桶}（因为方向相反，所以相加） = 25 + 5 = 30km/h$（这里的相对速度是指甲船相对于木桶的速度，由于它们都在水中，所以需要将水流的影响考虑在内）。
1小时后，甲船离木桶的距离为 $s_{甲} = v_{甲桶} × t = 30 × 1 = 30km$。
计算乙船离木桶的距离：
乙船顺流而行，其实际速度为船在静水中的速度加上水流速度，即 $v_{乙} = 30 + 5 = 35km/h$。
同样，木桶的速度为 $v_{桶} = 5km/h$。
但乙船和木桶是同向运动的，所以它们的相对速度为 $v_{乙桶} = v_{乙} - v_{桶} = 35 - 5 = 30km/h$（这里的相对速度是指乙船相对于木桶的速度）。
1小时后，乙船离木桶的距离也为 $s_{乙} = v_{乙桶} × t = 30 × 1 = 30km$。
【答案】：B

16. (新编)糖糖同学早上以2m/s的速度步行去学校,走了30min时,爸爸立即以10m/s的速度从家开车追上了糖糖,追上后糖糖搭上爸爸的车继续前进。到达学校,她发现比平时走路早到1min。糖糖在路上步行了37.5min才遇到爸爸的车,糖糖家到学校的距离为5700m。

答案： 解：设爸爸开车追上糖糖所用时间为$ t $秒。
糖糖先走30min（1800s）的路程：$ s_1 = v_1 t_1 = 2m/s × 1800s = 3600m $
爸爸追上糖糖时，糖糖共走的路程：$ s = s_1 + v_1 t = 3600m + 2m/s × t $
爸爸开车行驶的路程：$ s = v_2 t = 10m/s × t $
则$ 3600 + 2t = 10t $，解得$ t = 450s = 7.5min $
糖糖遇到爸爸时步行总时间：$ 30min + 7.5min = 37.5min $
设糖糖平时走路到学校需时间$ T $秒，家到学校距离为$ S $。
平时走路：$ S = v_1 T = 2T $
此次用时：$ t_总 = 1800s + 450s + \frac{S - s}{v_2} = 2250s + \frac{2T - 10 × 450}{10} $
已知此次比平时早到1min（60s），则$ T - t_总 = 60 $
即$ T - [2250 + \frac{2T - 4500}{10}] = 60 $，解得$ T = 2850s $
$ S = 2m/s × 2850s = 5700m $
37.5；5700