《2025年暑假作业快乐的假日七年级数学》

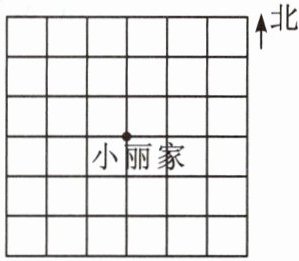
10. 从小丽家先向西走200 m,再向北走100 m到小玲家;从小丽家先向东走100 m,再向北走200 m到小娟家.已知小丽家的位置如图所示(每个小正方形的边长均为100 m).
(1)建立适当的平面直角坐标系,确定小玲家、小娟家的位置,并写出坐标;
(2)说明从小娟家去小玲家的走法.

答案：
解:
(1)建立平面直角坐标系如图所示:
　　　　　　　
小玲家(-200,100)　小娟家(100,200)　
(2)先向西走300m,再向南走100m.(或先向南走100m，再向西走300m)

11. 【阅读理解】若$a≠b$,规定符号$[a,b]$表示a,b两个数中较大的一个.规定符号$(a,b)$表示a,b两个数中较小的一个.
例如$[2,1]= 2,(2,1)= 1$.
【尝试应用】
(1)$[2,\sqrt {3}]= $______;$(-\frac {1}{2},-\frac {2}{3})= $______;
【拓广探索】
(2)若$[-2n-1,-2n+1]-(m,m+1)= 2$.求代数式$(m+2n)^{2024}-2m-4n+5$的值.

答案： 解:
(1)2 $-\frac{2}{3}$
(2)
∵[-2n-1,-2n+1]-(m,m+1)=2,
∴-2n+1-m=2,-2n-m=1,m+2n=-1,
∴(m+2n)^{2024}-2m-4n+5=(m+2n)^{2024}-2(m+2n)+5=(-1)^{2024}-2×(-1)+5=1+2+5=8.