《2025年暑假作业快乐的假日七年级数学》

1. $ x = - 3 $,$ y = 1 $为下列哪一个二元一次方程的解 ( )

A.$ x + 2 y = - 1 $
B.$ x - 2 y = 1 $
C.$ 2 x + 3 y = 6 $
D.$ 2 x - 3 y = - 6 $

答案： A

2. 在 $ 3.1415 $,$ \frac { 1 } { 7 } $,$ \frac { 8 } { 3 } $,$ 0 $,$ - \sqrt { 2 } $,$ - 0.89 $,$ \frac { \pi } { 3 } - 1 $,$ - 2011 $,$ 0.3030030003 … $(相邻两个 $ 3 $ 之间 $ 0 $ 的个数逐次加 $ 1 $),$ 5 + \sqrt { 7 } $ 中,无理数有 ( )

A.$ 2 $ 个
B.$ 3 $ 个
C.$ 4 $ 个
D.$ 5 $ 个

答案： C

3.(广西中考)如图,在平面直角坐标系中,点 $ O $ 为坐标原点,点 $ P $ 的坐标为 $ ( 2,1 ) $,则点 $ Q $ 的坐标为 ( )

A.$ ( 3,0 ) $
B.$ ( 0,2 ) $
C.$ ( 3,2 ) $
D.$ ( 1,2 ) $

答案： C

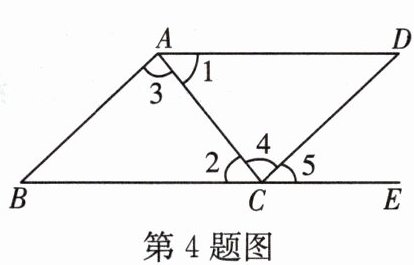
4. 如图,下列能判定 $ A B // C D $ 的条件有 ( )
(1)$ \angle B + \angle B C D = 180 ^ { \circ } $；(2)$ \angle 1 = \angle 2 $；(3)$ \angle 3 = \angle 4 $；(4)$ \angle B = \angle 5 $.
A. $ 1 $ 个 B. $ 2 $ 个 C. $ 3 $ 个 D. $ 4 $ 个

答案： C

5. 计算：$ \sqrt { 9 } - 2 + \sqrt [ 3 ] { 8 } - | - 2 | = $______.

答案： 1

6. 如图,已知 $ A C \perp B C $,$ C D \perp A B $,$ A C = 3 $,$ B C = 4 $,$ C D = 2.4 $,则点 $ C $ 到直线 $ A B $ 的距离等于______.

答案： 2.4

7. 若 $ 3 m - 5 x ^ { 3 + m } ＞ 4 $ 是关于 $ x $ 的一元一次不等式,则该不等式的解集是______.

答案： x＜−2

8.(上海中考)《九章算术》中有一道题的条件是：“今有大器五小器一容三斛,大器一小器五容二斛.”大致意思是：有大小两种盛米的桶,$ 5 $ 大桶加 $ 1 $ 小桶共盛 $ 3 $ 斛米,$ 1 $ 大桶加 $ 5 $ 小桶共盛 $ 2 $ 斛米.依据该条件,$ 1 $ 大桶加 $ 1 $ 小桶共盛______斛米.(注：斛是古代一种容量单位)

答案： $\frac{5}{6}$