《2025年暑假作业快乐的假日七年级数学》

8. (孝感中考)董永社区在创建全国卫生城市的活动中,随机检查了本社区部分住户五月份某周内“垃圾分类”的实施情况,将它们绘制了两幅不完整的统计图(A. 小于 5 天;B. 5 天;C. 6 天;D. 7 天),则扇形统计图 B 部分所对应的圆心角的度数是______.

答案： 【解析】：
本题可先根据A类住户的数量和其所占的百分比求出总户数，再求出B类住户所占的百分比，最后根据扇形圆心角的度数与百分比的关系求出扇形统计图B部分所对应的圆心角的度数。
步骤一：计算总户数
已知A类住户有$9$户，且A类住户在扇形统计图中所占的百分比为$15\%$，根据公式“总数$=$部分数量$÷$该部分所占百分比”，可得总户数为：$9÷15\% = 9÷0.15 = 60$（户）。
步骤二：计算B类住户的数量
由条形统计图可知A类住户有$9$户，C类住户有$21$户，D类住户有$12$户，总户数为$60$户，那么B类住户的数量为：$60 - 9 - 21 - 12 = 18$（户）。
步骤三：计算B类住户所占的百分比
根据公式“百分比$=$部分数量$÷$总数$×100\%$”，可得B类住户所占的百分比为：$18÷60×100\% = 0.3×100\% = 30\%$。
步骤四：计算扇形统计图B部分所对应的圆心角的度数
因为在扇形统计图中，圆心角的度数$ = 360^{\circ}×$该部分所占的百分比，所以扇形统计图B部分所对应的圆心角的度数为：$360^{\circ}×30\% = 360^{\circ}×0.3 = 108^{\circ}$。
【答案】：$108^{\circ}$

9. 如图,$∠AGF= ∠ABC,∠1+∠2= 180^{\circ }$.
(1)BF 与 DE 平行吗? 为什么?

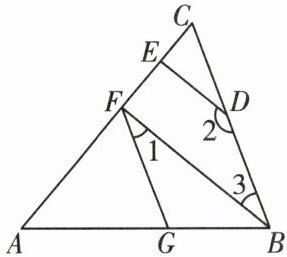
(2)若$BF⊥AC,∠2= 150^{\circ }$,求$∠AFG$的度数.

答案： 【解析】：
(1) 题目要求判断BF与DE是否平行。首先，由于$∠AGF=∠ABC$，根据同位角相等，两直线平行，可以得出$FG// BC$。接着，由于$∠1+∠2=180^{\circ}$，$∠1+∠3=180^{\circ}$，根据同角的补角相等，所以$∠2=∠3$，根据内错角相等，两直线平行，因此可以得出$BF// DE$。
(2) 题目给出了$BF⊥AC$和$∠2=150^{\circ}$，要求求解$∠AFG$的度数。首先，由于$BF// DE$和$BF⊥AC$，根据垂直的定义，$∠AFB=90^{\circ}$。然后，由于$∠1+∠2=180^{\circ}$和$∠2=150^{\circ}$，可以得出$∠1=30^{\circ}$。最后，根据$∠AFG=∠AFB-∠1$，可以得出$∠AFG=90^{\circ}-30^{\circ}=60^{\circ}$。
【答案】：
(1) 解：$BF// DE$。
理由如下：
∵$∠AGF=∠ABC$，
∴$FG// BC$，
∵$∠1+∠2=180^{\circ}$，$∠1+∠3=180^{\circ}$，
∴$∠2=∠3$，
∴$BF// DE$；
(2) 解：
∵$BF// DE$，$BF⊥AC$，
∴$∠AFB=∠ADE=90^{\circ}$，
∵$∠1+∠2=180^{\circ}$，$∠2=150^{\circ}$，
∴$∠1=30^{\circ}$，
∴$∠AFG=∠AFB-∠1=90^{\circ}-30^{\circ}=60^{\circ}$。

10. 某中学七年级(1)班去体育用品商店买一些篮球和排球,供班上同学进行体育锻炼时使用,共买了 2 个篮球和 6 个排球,花费 570 元,并且每个排球比篮球便宜 25 元.
(1)求篮球和排球的单价各是多少;
(2)商店里搞活动,有两种套餐,①套餐打折:五个篮球和五个排球为一套餐,套餐打八折;②满减活动:满 999 减 100,满 1 999 减 200. 两种活动不重复参与,学校打算购买 14 个篮球,12 个排球,请问如何安排更划算?

答案： （2）若按照①套餐打折购买费用为$2×(5×90+5×65)×0.8+4×90+2×65=1730$(元)；若参加②满减活动购买费用为$14×90+12×65=2040$(元).$\because2040＞1999$，$\therefore2040-200=1840$(元).又$\because1840＞1730$，$\therefore$选择套餐①所花费用比选择套餐②所花费用低.答:选用套餐①购买更划算.