《2025年暑假作业快乐的假日七年级数学》

8.已知不等式$2x-a≤0$的正整数解恰好是 1,2,3,4,5,那么 a 的取值范围是______.

答案： 【解析】：
本题主要考查一元一次不等式的解集以及如何根据解集确定参数的取值范围。
首先，我们解不等式$2x - a \leq 0$，得到$x \leq \frac{a}{2}$。
由题意知，这个不等式的正整数解恰好是$1，2，3，4，5$。
这意味着$\frac{a}{2}$应当大于等于$5$（以包含$5$这个解），同时小于$6$（以排除$6$这个非解）。
因此，我们可以列出以下不等式组来确定$a$的取值范围：
$\begin{cases}\frac{a}{2} \geq 5, \\frac{a}{2} ＜ 6.\end{cases}$
解这个不等式组，我们得到：
$\begin{cases}a \geq 10, \\a ＜ 12.\end{cases}$
综合以上两个不等式，我们得到$a$的取值范围是$10 \leq a ＜ 12$。
【答案】：
$10 \leq a ＜ 12$。

9.(淄博中考)如图,已知 A,B 两点的坐标分别为$A(-3,1),B(-1,3)$,将线段AB 平移得到线段 CD.若点 A 的对应点是$C(1,2)$,则点 B 的对应点 D 的坐标是______.

答案： 【解析】：
本题考查坐标与图形的平移。
在平面直角坐标系中，图形的平移与图形上点的平移规律相同。
点$A(-3,1)$的对应点是$C(1,2)$，横坐标的变化为$1-(-3)=4$，纵坐标的变化为$2 - 1 = 1$，即点$A$向右平移$4$个单位长度，向上平移$1$个单位长度得到点$C$。
因为线段$AB$平移得到线段$CD$，所以点$B$的平移规律与点$A$相同，也是向右平移$4$个单位长度，向上平移$1$个单位长度。
已知$B(-1,3)$，那么点$B$向右平移$4$个单位长度，横坐标变为$-1 + 4 = 3$；向上平移$1$个单位长度，纵坐标变为$3 + 1 = 4$。
所以点$D$的坐标是$(3,4)$。
【答案】：
$(3,4)$

10.“昔锦官之地,有匠作弓与箭.作一弓需三日,作一箭需二日.共费四十日,成弓箭十五.”题目大意是:从前在锦官城这个地方,有工匠制作弓和箭.制作一张弓需要三天时间,制作一支箭需要两天时间.总共花费四十天时间,制成弓和箭共计十五件.设弓有x件,箭有y件,则可列方程组为______.

答案： 【解析】：
这是一个典型的线性方程组问题，需要用到线性方程组的解法来求解。
题目中给出了两个关键信息：
总共花费四十天时间。
制成弓和箭共计十五件。
根据题目，可以设弓有$x$件，箭有$y$件。
根据“制作一张弓需要三天时间，制作一支箭需要两天时间，总共花费四十天时间”这一信息，可以列出第一个方程：
$3x + 2y = 40$，
这个方程表示制作弓和箭所花费的总时间。
根据“制成弓和箭共计十五件”这一信息，可以列出第二个方程：
$x + y = 15$，
这个方程表示弓和箭的总数量。
所以，我们可以列出方程组为：
$\left\{ \begin{array}{l} 3x + 2y = 40, \\ x + y = 15. \end{array} \right.$
【答案】：
$\left\{ \begin{array}{l} 3x + 2y = 40, \\ x + y = 15. \end{array} \right.$

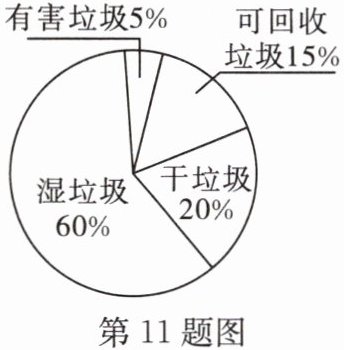
11.(上海中考)小明为了解所在小区居民各类生活垃圾的投放情况,他随机调查了该小区 50 户家庭某一天各类生活垃圾的投放量,统计得出这 50 户家庭各类生活垃圾的投放总量是 100 kg,并画出各类生活垃圾投放量分布情况的扇形图(如图所示),根据以上信息,估计该小区 300 户居民这一天投放的可回收垃圾共约______kg.

答案： 【解析】：
本题考查利用扇形图的信息，通过比例计算来求解问题。
首先，从扇形图中找到可回收垃圾所占的比例，为$15\%$。
然后，根据题目信息，50户家庭各类生活垃圾的投放总量是 100 kg。
因此，50户家庭投放的可回收垃圾量约为 $100 × 15\% = 15（kg）$。
最后，由于需要估计的是300户居民的可回收垃圾投放量，而调查的是50户家庭，所以需要将50户家庭的投放量按比例放大到300户。
即：$300 ÷ 50 × 15 = 6 × 15 = 90（kg）$。
【答案】：90 kg。

12.已知$2a-1$的立方根是 3,$3a+b+6$的算术平方根是 7,求$a+2b$的平方根.

答案： 【解析】：
本题主要考查立方根与平方根的定义和性质，以及代数方程的解法。
首先，根据题目条件，$2a-1$的立方根是3，那么我们可以根据立方根的定义列出方程：
$\sqrt[3]{2a - 1} = 3$，
对方程两边同时立方，得到：
$2a - 1 = 3^3$，
$2a - 1 = 27$，
解得：
$a = 14$。
接着，根据题目条件，$3a+b+6$的算术平方根是7，那么我们可以根据平方根的定义列出方程：
$\sqrt{3a + b + 6} = 7$，
对方程两边同时平方，得到：
$3a + b + 6 = 7^2$，
$3a + b + 6 = 49$，
将$a=14$代入上式，得到：
$3 × 14 + b + 6 = 49$，
$42 + b + 6 = 49$，
解得：
$b = 1$。
最后，我们需要求$a+2b$的平方根，代入$a=14$，$b=1$，得到：
$a + 2b = 14 + 2 × 1 = 16$，
所以，$a+2b$的平方根是$\pm \sqrt{16} = \pm 4$。
【答案】：
$\pm 4$。

13.已知关于x,y的方程组$\left\{\begin{array}{l} x+2y= 1,\\ x-2y= m\end{array} \right. $的解都小于 1,且关于 x 的不等式组$\left\{\begin{array}{l} \frac {1}{5}x+2≥1,\\ 2n-x≥1\end{array} \right. $无解.
(1)分别求出 m 和 n 的取值范围;
(2)化简:$|m+3|+|1-m|+|n+2|$.

答案： 【解析】：
本题主要考查了二元一次方程组的解法，一元一次不等式组的解法以及绝对值的性质。
(1)对于方程组：
$\left\{\begin{array}{l}x + 2y = 1, \\x - 2y = m,\end{array}\right.$
将两个方程相加，得到：
$2x = 1 + m \implies x = \frac{1 + m}{2}$，
将两个方程相减，得到：
$4y = 1 - m \implies y = \frac{1 - m}{4}$，
根据题目条件，$x$ 和 $y$ 都小于 1，即：
$\frac{1 + m}{2} ＜ 1 \implies m ＜ 1$，
$\frac{1 - m}{4} ＜ 1 \implies m ＞ -3$，
综合这两个不等式，得到 $m$ 的取值范围为 $-3 ＜ m ＜ 1$。
对于不等式组：
$\left\{\begin{array}{l}\frac{1}{5}x + 2 \geq 1, \\2n - x \geq 1,\end{array}\right.$
解第一个不等式，得到：
$x \geq -5$，
解第二个不等式，得到：
$x \leq 2n - 1$，
由于不等式组无解，因此有：
$2n - 1 ＜ -5 \implies n ＜-2$，
但考虑到$x$的取值范围，我们得到$n$的实际取值范围应为$n \leq-2$（当$n=-2$时，$x\leq -5$和$x\geq -5$，此时$x$只能取$-5$，但题目要求不等式组无解，所以$n$不能取$-2$，只能是$n＜-2$），综合后得到 $-3 ＜ m ＜ 1$，$n ＜ -2$。
(2)对于绝对值表达式 $|m + 3| + |1 - m| + |n + 2|$，
由于 $-3 ＜ m ＜ 1$，则 $m + 3 ＞ 0$，$1 - m ＞ 0$，
又因为$n＜-2$，则$n + 2＜0$，
所以，$|m + 3| = m + 3$，$|1 - m| = 1 - m$，$|n + 2| =-(n + 2)$，
代入原式，得到：
$|m + 3| + |1 - m| + |n + 2| = (m + 3) + (1 - m) - (n + 2) = 2 - n$。
【答案】：
(1) $m$ 的取值范围是 $-3 ＜ m ＜ 1$，$n$ 的取值范围是 $n ＜ -2$；
(2) $|m + 3| + |1 - m| + |n + 2| = 2 - n$。