第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
8.如图,在平面直角坐标系中,三角形ABC的面积为2,三个顶点的坐标分别为A(3,2),B(1,1),C(a,b),且a,b均为正整数,则点C的坐标为______.
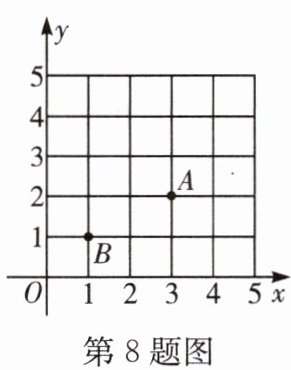

答案:
(5,1),(1,3),(3,4),(5,5)
9.(自贡中考)某活动小组购买了4个篮球和5个足球,一共花费了466元,其中篮球的单价比足球的单价多4元,求篮球的单价和足球的单价.设篮球的单价为x元,足球的单价为y元,依题意,可列方程组为______.
答案:
$\begin{cases} x-y=4, \\ 4x+5y=466 \end{cases}$
10.若$(x - 2024)^2 + √{y + 2025} = 0,$求x + y的立方根.
答案:
解:由题意,得$\begin{cases} x-2024=0, \\ y+2025=0 \end{cases}$解得$\begin{cases} x=2024, \\ y=-2025 \end{cases}$$\therefore x+y=$2024-2025=-1.$\therefore \sqrt[3]{x+y}=\sqrt[3]{-1}=-1$.即$x+y$的立方根是-1.
11.如图,已知直线AB和CD相交于点O,CO⊥EO,OF平分∠AOE.
(1)∠AOC的对顶角是______;∠EOF的余角是______;
(2)若∠BOD= 40°,求∠COF.
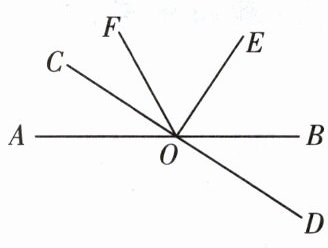
(1)∠AOC的对顶角是______;∠EOF的余角是______;
(2)若∠BOD= 40°,求∠COF.

答案:
解:
(1)$\angle BOD$ $\angle COF$
(2)$\because OE\perp CD$,$\therefore \angle EOC=90^{\circ}$.$\because \angle AOC=\angle BOD=40^{\circ}$,$\therefore \angle AOE=\angle AOC+\angle COE=40^{\circ}+90^{\circ}=130^{\circ}$.$\because OF$平分$\angle AOE$,$\therefore \angle AOF=\frac{1}{2}\angle AOE=65^{\circ}$,$\therefore \angle COF=\angle AOF-\angle AOC=65^{\circ}-40^{\circ}=25^{\circ}$.
(1)$\angle BOD$ $\angle COF$
(2)$\because OE\perp CD$,$\therefore \angle EOC=90^{\circ}$.$\because \angle AOC=\angle BOD=40^{\circ}$,$\therefore \angle AOE=\angle AOC+\angle COE=40^{\circ}+90^{\circ}=130^{\circ}$.$\because OF$平分$\angle AOE$,$\therefore \angle AOF=\frac{1}{2}\angle AOE=65^{\circ}$,$\therefore \angle COF=\angle AOF-\angle AOC=65^{\circ}-40^{\circ}=25^{\circ}$.
12.(山西中考)为加强校园消防安全,学校计划购买某种型号的水基灭火器和干粉灭火器共50个.其中水基灭火器的单价为540元/个,干粉灭火器的单价为380元/个.若学校购买这两种灭火器的总价不超过21000元,则最多可购买这种型号的水基灭火器多少个?


答案:
解:设可购买这种型号的水基灭火器$x$个,则购买干粉灭火器$(50-x)$个.根据题意,得$540x+380(50-x)\leq 21000$,解得$x\leq 12.5$.$\because x$为整数,$\therefore x$取最大值为12.答:最多可购买这种型号的水基灭火器12个.
查看更多完整答案,请扫码查看


