第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
8.(广东中考)关于x的不等式组中,两个不等式的解集如图所示,则这个不等式组的解集是______.
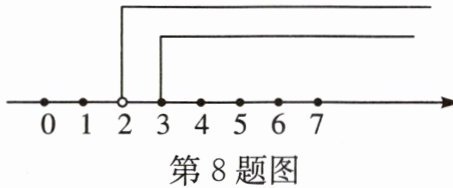

答案:
x≥ 3
9.如图,点 E 是 AD 延长线上一点,如果添加一个条件,使$BC// AD$,则可添加的条件为______.(任意添加一个符合题意的条件即可)


答案:
∠A+∠ABC=180°(答案不唯一)
10.计算:(1)$|1-\sqrt {2}|+|\sqrt {2}-\sqrt {3}|+|\sqrt {2}-1|;$
(2)$\sqrt [3]{-8}-(2+\sqrt {2})+\frac {1}{2}(\sqrt {16}-\sqrt {2})-|-3|.$
(2)$\sqrt [3]{-8}-(2+\sqrt {2})+\frac {1}{2}(\sqrt {16}-\sqrt {2})-|-3|.$
答案:
解:
(1)原式$=-(1-\sqrt {2})-(\sqrt {2}-\sqrt {3})+(\sqrt {2}-1)=-1+\sqrt {2}-\sqrt {2}+\sqrt {3}+\sqrt {2}-1=\sqrt {3}+\sqrt {2}-2. (2)$原式$=-2-(2+\sqrt {2})+\frac {1}{2}(4-\sqrt {2})-3=-2-2-\sqrt {2}+2-\frac {\sqrt {2}}{2}-3=-5-\frac {3\sqrt {2}}{2}.$
(1)原式$=-(1-\sqrt {2})-(\sqrt {2}-\sqrt {3})+(\sqrt {2}-1)=-1+\sqrt {2}-\sqrt {2}+\sqrt {3}+\sqrt {2}-1=\sqrt {3}+\sqrt {2}-2. (2)$原式$=-2-(2+\sqrt {2})+\frac {1}{2}(4-\sqrt {2})-3=-2-2-\sqrt {2}+2-\frac {\sqrt {2}}{2}-3=-5-\frac {3\sqrt {2}}{2}.$
11.(安徽中考)乡村振兴战略实施以来,很多外出人员返乡创业.某村有部分返乡青年承包了一些田地,采用新技术种植 A,B 两种农作物.种植这两种农作物每公顷所需人数和投入资金如下表:
|农作物品种|每公顷所需人数|每公顷所需投入资金(万元)|
|A|4|8|
|B|3|9|
已知农作物种植人员共 24 位,且每人只参与一种农作物种植,投入资金共 60 万元,问 A,B 这两种农作物的种植面积各多少公顷?
|农作物品种|每公顷所需人数|每公顷所需投入资金(万元)|
|A|4|8|
|B|3|9|
已知农作物种植人员共 24 位,且每人只参与一种农作物种植,投入资金共 60 万元,问 A,B 这两种农作物的种植面积各多少公顷?
答案:
【解析】:
本题考查的是二元一次方程组的应用。
设A种农作物的种植面积为$x$公顷,B种农作物的种植面积为$y$公顷。
根据题目描述,可以建立以下两个方程:
根据每公顷所需人数:
A种农作物每公顷需要4人,B种农作物每公顷需要3人,总人数为24人,所以方程为:$4x + 3y = 24$。
根据每公顷所需投入资金:
A种农作物每公顷需要8万元,B种农作物每公顷需要9万元,总投入资金为60万元,所以方程为:$8x + 9y = 60$。
接下来,解这个二元一次方程组:
从第一个方程中解出$y$:$y = \frac{24 - 4x}{3}$。
将这个表达式代入第二个方程中:$8x + 9(\frac{24 - 4x}{3}) = 60$。
解这个方程,得到:$x = 3$。
将$x = 3$代入第一个方程中,得到:$y = 4 - \frac{4 × 3}{3} = 4$。
所以,方程组的解为:$x = 3$,$y = 4$。
【答案】:
A种农作物的种植面积为3公顷,B种农作物的种植面积为4公顷。
本题考查的是二元一次方程组的应用。
设A种农作物的种植面积为$x$公顷,B种农作物的种植面积为$y$公顷。
根据题目描述,可以建立以下两个方程:
根据每公顷所需人数:
A种农作物每公顷需要4人,B种农作物每公顷需要3人,总人数为24人,所以方程为:$4x + 3y = 24$。
根据每公顷所需投入资金:
A种农作物每公顷需要8万元,B种农作物每公顷需要9万元,总投入资金为60万元,所以方程为:$8x + 9y = 60$。
接下来,解这个二元一次方程组:
从第一个方程中解出$y$:$y = \frac{24 - 4x}{3}$。
将这个表达式代入第二个方程中:$8x + 9(\frac{24 - 4x}{3}) = 60$。
解这个方程,得到:$x = 3$。
将$x = 3$代入第一个方程中,得到:$y = 4 - \frac{4 × 3}{3} = 4$。
所以,方程组的解为:$x = 3$,$y = 4$。
【答案】:
A种农作物的种植面积为3公顷,B种农作物的种植面积为4公顷。
查看更多完整答案,请扫码查看


