2025年赢在暑假抢分计划七年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年赢在暑假抢分计划七年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. (1)如图 1,已知 $ AB // CD $,试说明 $ \angle AEP + \angle CFP = \angle EPF $;
(2)如图 2,$ AB // CD $,请写出 $ \angle AEP $,$ \angle EPF $,$ \angle CFP $之间的数量关系,并说明理由.
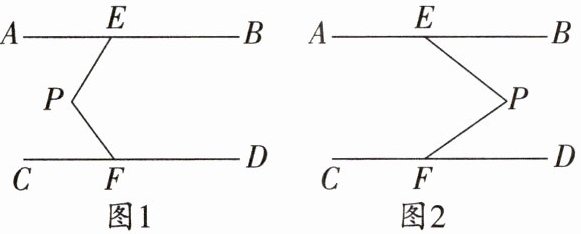
(2)如图 2,$ AB // CD $,请写出 $ \angle AEP $,$ \angle EPF $,$ \angle CFP $之间的数量关系,并说明理由.
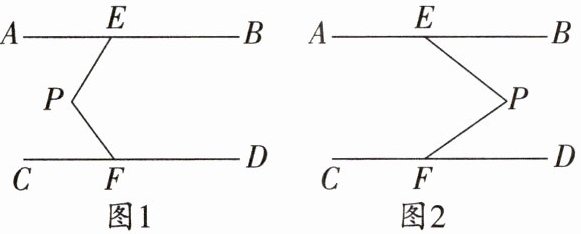
答案:
解:
(1)如图 1,过点 P 作 $PG // AB$。因为 $AB // CD$,所以 $PG // CD$,所以 $ \angle AEP = \angle 1$,$ \angle CFP = \angle 2$。又因为 $ \angle 1 + \angle 2 = \angle EPF$,所以 $ \angle AEP + \angle CFP = \angle EPF$;
(2)如图 2,过点 P 作 $PG // AB$。因为 $AB // CD$,所以 $PG // CD$,所以 $ \angle AEP + \angle GPE = 180^{\circ}$,$ \angle CFP + \angle GPF = 180^{\circ}$,所以 $ \angle AEP + \angle GPE + \angle CFP + \angle GPF = 360^{\circ}$。又因为 $ \angle GPE + \angle GPF = \angle EPF$,所以 $ \angle AEP + \angle EPF + \angle CFP = 360^{\circ}$。

解:
(1)如图 1,过点 P 作 $PG // AB$。因为 $AB // CD$,所以 $PG // CD$,所以 $ \angle AEP = \angle 1$,$ \angle CFP = \angle 2$。又因为 $ \angle 1 + \angle 2 = \angle EPF$,所以 $ \angle AEP + \angle CFP = \angle EPF$;
(2)如图 2,过点 P 作 $PG // AB$。因为 $AB // CD$,所以 $PG // CD$,所以 $ \angle AEP + \angle GPE = 180^{\circ}$,$ \angle CFP + \angle GPF = 180^{\circ}$,所以 $ \angle AEP + \angle GPE + \angle CFP + \angle GPF = 360^{\circ}$。又因为 $ \angle GPE + \angle GPF = \angle EPF$,所以 $ \angle AEP + \angle EPF + \angle CFP = 360^{\circ}$。

2. 已知 $ AB // CD $,点 $ E $,$ F $分别在 $ AB $,$ CD $上,点 $ O $在 $ AB $,$ CD $之间,$ O $,$ B $,$ D $三点均在直线 $ EF $的同侧.
(1)如图 1,试说明:$ \angle EOF = \angle BEO + \angle DFO $;
(2)如图 2,若 $ OE \perp OF $,$ EG $,$ FG $分别平分 $ \angle BEO $和 $ \angle DFO $,求 $ \angle G $的度数;
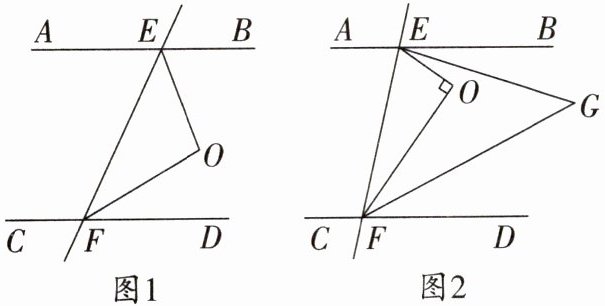
(3)如图 3,若 $ \angle EOF $的度数为 $ \alpha $,$ EM $平分 $ \angle BEO $交 $ FO $的延长线于点 $ M $,$ FN $平分 $ \angle DFO $交 $ EO $的延长线于点 $ N $,求 $ \angle M + \angle N $的度数(用含 $ \alpha $的式子表示).

(1)如图 1,试说明:$ \angle EOF = \angle BEO + \angle DFO $;
(2)如图 2,若 $ OE \perp OF $,$ EG $,$ FG $分别平分 $ \angle BEO $和 $ \angle DFO $,求 $ \angle G $的度数;

(3)如图 3,若 $ \angle EOF $的度数为 $ \alpha $,$ EM $平分 $ \angle BEO $交 $ FO $的延长线于点 $ M $,$ FN $平分 $ \angle DFO $交 $ EO $的延长线于点 $ N $,求 $ \angle M + \angle N $的度数(用含 $ \alpha $的式子表示).

答案:
解:
(1)过点 O 向左作 $OP // AB$,则 $ \angle EOP = \angle BEO$。因为 $OP // AB$,$AB // CD$,所以 $OP // CD$。所以 $ \angle FOP = \angle DFO$。所以 $ \angle EOF = \angle EOP + \angle FOP = \angle BEO + \angle DFO$;
(2)因为 $OE \perp OF$,所以 $ \angle EOF = 90^{\circ}$。由
(1)知 $ \angle BEO + \angle DFO = 90^{\circ}$,$ \angle G = \angle BEG + \angle DFG$。因为 EG,FG 分别平分 $ \angle BEO$ 和 $ \angle DFO$,所以 $ \angle G = \angle BEG + \angle DFG = \frac{1}{2}(\angle BEO + \angle DFO) = \frac{1}{2}\angle EOF = \frac{1}{2} × 90^{\circ} = 45^{\circ}$;
(3)设 $ \angle BEO$ 的度数为 x,$ \angle DFO$ 的度数为 y,则由
(1)得 $x + y = \alpha$。由
(1)
(2)得 $ \angle M = \angle BEM + \angle DFM = \frac{1}{2}x + y$ ①,$ \angle N = \angle BEN + \angle DFN = x + \frac{1}{2}y$ ②。① + ②得 $ \angle M + \angle N = \frac{3}{2}(x + y) = \frac{3}{2}\alpha$。
(1)过点 O 向左作 $OP // AB$,则 $ \angle EOP = \angle BEO$。因为 $OP // AB$,$AB // CD$,所以 $OP // CD$。所以 $ \angle FOP = \angle DFO$。所以 $ \angle EOF = \angle EOP + \angle FOP = \angle BEO + \angle DFO$;
(2)因为 $OE \perp OF$,所以 $ \angle EOF = 90^{\circ}$。由
(1)知 $ \angle BEO + \angle DFO = 90^{\circ}$,$ \angle G = \angle BEG + \angle DFG$。因为 EG,FG 分别平分 $ \angle BEO$ 和 $ \angle DFO$,所以 $ \angle G = \angle BEG + \angle DFG = \frac{1}{2}(\angle BEO + \angle DFO) = \frac{1}{2}\angle EOF = \frac{1}{2} × 90^{\circ} = 45^{\circ}$;
(3)设 $ \angle BEO$ 的度数为 x,$ \angle DFO$ 的度数为 y,则由
(1)得 $x + y = \alpha$。由
(1)
(2)得 $ \angle M = \angle BEM + \angle DFM = \frac{1}{2}x + y$ ①,$ \angle N = \angle BEN + \angle DFN = x + \frac{1}{2}y$ ②。① + ②得 $ \angle M + \angle N = \frac{3}{2}(x + y) = \frac{3}{2}\alpha$。
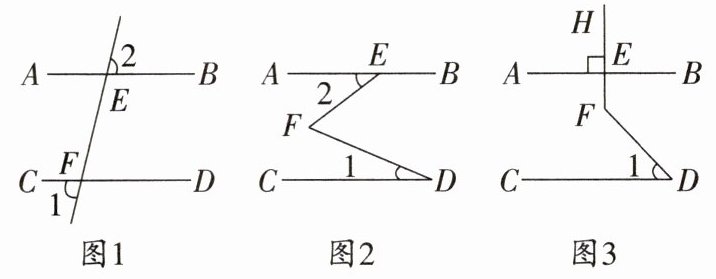
3. 如图,已知 $ AB // CD $.
(1)如图 1,$ EF $分别和 $ AB $,$ CD $相交于点 $ E $,$ F $,试说明 $ \angle 1 = \angle 2 $;
(2)如图 2,试猜想 $ \angle 1 $,$ \angle 2 $,$ \angle EFD $之间有什么数量关系,并说明理由;
(3)如图 3,若 $ FH \perp AB $于点 $ E $,$ \angle 1 = 40^{\circ} $,求 $ \angle EFD $的度数.
(1)如图 1,$ EF $分别和 $ AB $,$ CD $相交于点 $ E $,$ F $,试说明 $ \angle 1 = \angle 2 $;
(2)如图 2,试猜想 $ \angle 1 $,$ \angle 2 $,$ \angle EFD $之间有什么数量关系,并说明理由;
(3)如图 3,若 $ FH \perp AB $于点 $ E $,$ \angle 1 = 40^{\circ} $,求 $ \angle EFD $的度数.

答案:
解:
(1)因为 $AB // CD$,所以 $ \angle 2 = \angle EFD$。因为 $ \angle 1 = \angle EFD$,所以 $ \angle 1 = \angle 2$;
(2)猜想的结论是:$ \angle 1 + \angle 2 = \angle EFD$。理由:如图 1,过点 F 作 $FG // AB$。因为 $FG // AB$,$AB // CD$,所以 $AB // FG // CD$,所以 $ \angle 1 = \angle DFG$,$ \angle 2 = \angle EFG$,所以 $ \angle 1 + \angle 2 = \angle DFG + \angle EFG$。因为 $ \angle DFG + \angle EFG = \angle EFD$,所以 $ \angle 1 + \angle 2 = \angle EFD$;
(3)如图 2,过点 F 作 $FG // AB$。因为 $FG // AB$,$AB // CD$,所以 $AB // FG // CD$。所以 $ \angle EFG = \angle AEF$,$ \angle DFG = \angle 1 = 40^{\circ}$。因为 $FH \perp AB$,所以 $ \angle AEF = 90^{\circ}$,所以 $ \angle EFG = 90^{\circ}$。所以 $ \angle EFD = \angle EFG + \angle DFG = 90^{\circ} + 40^{\circ} = 130^{\circ}$。

解:
(1)因为 $AB // CD$,所以 $ \angle 2 = \angle EFD$。因为 $ \angle 1 = \angle EFD$,所以 $ \angle 1 = \angle 2$;
(2)猜想的结论是:$ \angle 1 + \angle 2 = \angle EFD$。理由:如图 1,过点 F 作 $FG // AB$。因为 $FG // AB$,$AB // CD$,所以 $AB // FG // CD$,所以 $ \angle 1 = \angle DFG$,$ \angle 2 = \angle EFG$,所以 $ \angle 1 + \angle 2 = \angle DFG + \angle EFG$。因为 $ \angle DFG + \angle EFG = \angle EFD$,所以 $ \angle 1 + \angle 2 = \angle EFD$;
(3)如图 2,过点 F 作 $FG // AB$。因为 $FG // AB$,$AB // CD$,所以 $AB // FG // CD$。所以 $ \angle EFG = \angle AEF$,$ \angle DFG = \angle 1 = 40^{\circ}$。因为 $FH \perp AB$,所以 $ \angle AEF = 90^{\circ}$,所以 $ \angle EFG = 90^{\circ}$。所以 $ \angle EFD = \angle EFG + \angle DFG = 90^{\circ} + 40^{\circ} = 130^{\circ}$。

查看更多完整答案,请扫码查看


