例 7 【思考尝试】(1)数学活动课上,老师出了一个问题:如图 1,在矩形 $ABCD$ 中,$E$ 是边 $AB$ 上一点,$DF\perp CE$ 于点 $F$,$GD\perp DF$,$AG\perp DG$,$AG = CF$,试说明矩形 $ABCD$ 是正方形。
【实践探究】(2)小睿受此问题启发,逆向思考并提出新的问题:如图 2,在正方形 $ABCD$ 中,$E$ 是边 $AB$ 上一点,$DF\perp CE$ 于点 $F$,$AH\perp CE$ 交 $CE$ 的延长线于点 $H$,$GD\perp DF$,交 $HA$ 的延长线于点 $G$,可以用等式表示线段 $FH$,$AH$,$CF$ 的数量关系,请你思考并说明理由。

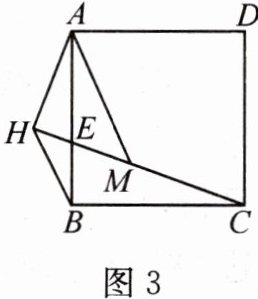
【拓展迁移】(3)小博深入研究小睿提出的这个问题,发现并提出新的探究点:如图 3,在正方形 $ABCD$ 中,$E$ 是边 $AB$ 上一点,$AH\perp CE$ 交 $CE$ 的延长线于点 $H$,点 $M$ 在 $CH$ 上,且 $AH = HM$,连接 $AM$,$BH$,可以用等式表示线段 $CM$,$BH$ 的数量关系,请你思考并说明理由。
【实践探究】(2)小睿受此问题启发,逆向思考并提出新的问题:如图 2,在正方形 $ABCD$ 中,$E$ 是边 $AB$ 上一点,$DF\perp CE$ 于点 $F$,$AH\perp CE$ 交 $CE$ 的延长线于点 $H$,$GD\perp DF$,交 $HA$ 的延长线于点 $G$,可以用等式表示线段 $FH$,$AH$,$CF$ 的数量关系,请你思考并说明理由。

【拓展迁移】(3)小博深入研究小睿提出的这个问题,发现并提出新的探究点:如图 3,在正方形 $ABCD$ 中,$E$ 是边 $AB$ 上一点,$AH\perp CE$ 交 $CE$ 的延长线于点 $H$,点 $M$ 在 $CH$ 上,且 $AH = HM$,连接 $AM$,$BH$,可以用等式表示线段 $CM$,$BH$ 的数量关系,请你思考并说明理由。

答案:
(1)证明矩形$ABCD$是正方形
- 因为$GD\perp DF$,$AG\perp DG$,$DF\perp CE$,所以$\angle G=\angle GDF = \angle DFC = 90^{\circ}$。
- 则$\angle GDA+\angle ADF = 90^{\circ}$,$\angle CDF+\angle ADF = 90^{\circ}$,所以$\angle GDA=\angle CDF$。
- 在$\triangle AGD$和$\triangle DFC$中,$\begin{cases}\angle G=\angle DFC\\\angle GDA=\angle CDF\\AG = CF\end{cases}$,根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等)可得$\triangle AGD\cong\triangle DFC$。
- 所以$AD = DC$。
- 又因为四边形$ABCD$是矩形,一组邻边相等的矩形是正方形,所以矩形$ABCD$是正方形。
(2)探究$FH$,$AH$,$CF$的数量关系
- 解:$FH=CF + AH$。
- 理由:因为$GD\perp DF$,$AH\perp CE$,$DF\perp CE$,所以$\angle G=\angle GFH=\angle DFC = 90^{\circ}$。
- 则$\angle GDA+\angle ADF = 90^{\circ}$,$\angle CDF+\angle ADF = 90^{\circ}$,所以$\angle GDA=\angle CDF$。
- 因为四边形$ABCD$是正方形,所以$AD = DC$。
- 由$\angle G=\angle DFC$,$\angle GDA=\angle CDF$,$AD = DC$,根据$AAS$可得$\triangle AGD\cong\triangle DFC$,所以$AG = DF$,$GD=CF$。
- 又因为$\angle G=\angle GFH=\angle AHF = 90^{\circ}$,所以四边形$GDFH$是矩形,则$GD = FH$,$AG = DF = AH$(矩形对边相等,全等三角形对应边相等)。
- 因为$GD=CF$,所以$FH=CF + AH$。
(3)探究$CM$,$BH$的数量关系
- 解:$CM=\sqrt{2}BH$。
- 理由:因为四边形$ABCD$是正方形,所以$AB = BC$,$\angle ABC = 90^{\circ}$。
- 因为$AH\perp CE$,$AH = HM$,所以$\angle HAM=\angle HMA = 45^{\circ}$,$\angle BAH+\angle EAM = 45^{\circ}$。
- 又因为$\angle BCM+\angle EAM=\angle AMC - \angle ABC=45^{\circ}$(三角形外角性质:三角形的一个外角等于不相邻的两个内角和),所以$\angle BAH=\angle BCM$。
- 在$\triangle ABH$和$\triangle BCM$中,$\begin{cases}\angle BAH=\angle BCM\\AB = BC\\\angle ABH=\angle BCM + 90^{\circ}=\angle ABC+\angle BAH=\angle ABM\end{cases}$,根据$ASA$(两角及其夹边对应相等的两个三角形全等)可得$\triangle ABH\cong\triangle BCM$。
- 所以$BH = CM\sin45^{\circ}$,即$CM=\sqrt{2}BH$。
综上,(1)通过证明三角形全等得出邻边相等,进而证明矩形是正方形;(2)$FH=CF + AH$;(3)$CM=\sqrt{2}BH$。
- 因为$GD\perp DF$,$AG\perp DG$,$DF\perp CE$,所以$\angle G=\angle GDF = \angle DFC = 90^{\circ}$。
- 则$\angle GDA+\angle ADF = 90^{\circ}$,$\angle CDF+\angle ADF = 90^{\circ}$,所以$\angle GDA=\angle CDF$。
- 在$\triangle AGD$和$\triangle DFC$中,$\begin{cases}\angle G=\angle DFC\\\angle GDA=\angle CDF\\AG = CF\end{cases}$,根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等)可得$\triangle AGD\cong\triangle DFC$。
- 所以$AD = DC$。
- 又因为四边形$ABCD$是矩形,一组邻边相等的矩形是正方形,所以矩形$ABCD$是正方形。
(2)探究$FH$,$AH$,$CF$的数量关系
- 解:$FH=CF + AH$。
- 理由:因为$GD\perp DF$,$AH\perp CE$,$DF\perp CE$,所以$\angle G=\angle GFH=\angle DFC = 90^{\circ}$。
- 则$\angle GDA+\angle ADF = 90^{\circ}$,$\angle CDF+\angle ADF = 90^{\circ}$,所以$\angle GDA=\angle CDF$。
- 因为四边形$ABCD$是正方形,所以$AD = DC$。
- 由$\angle G=\angle DFC$,$\angle GDA=\angle CDF$,$AD = DC$,根据$AAS$可得$\triangle AGD\cong\triangle DFC$,所以$AG = DF$,$GD=CF$。
- 又因为$\angle G=\angle GFH=\angle AHF = 90^{\circ}$,所以四边形$GDFH$是矩形,则$GD = FH$,$AG = DF = AH$(矩形对边相等,全等三角形对应边相等)。
- 因为$GD=CF$,所以$FH=CF + AH$。
(3)探究$CM$,$BH$的数量关系
- 解:$CM=\sqrt{2}BH$。
- 理由:因为四边形$ABCD$是正方形,所以$AB = BC$,$\angle ABC = 90^{\circ}$。
- 因为$AH\perp CE$,$AH = HM$,所以$\angle HAM=\angle HMA = 45^{\circ}$,$\angle BAH+\angle EAM = 45^{\circ}$。
- 又因为$\angle BCM+\angle EAM=\angle AMC - \angle ABC=45^{\circ}$(三角形外角性质:三角形的一个外角等于不相邻的两个内角和),所以$\angle BAH=\angle BCM$。
- 在$\triangle ABH$和$\triangle BCM$中,$\begin{cases}\angle BAH=\angle BCM\\AB = BC\\\angle ABH=\angle BCM + 90^{\circ}=\angle ABC+\angle BAH=\angle ABM\end{cases}$,根据$ASA$(两角及其夹边对应相等的两个三角形全等)可得$\triangle ABH\cong\triangle BCM$。
- 所以$BH = CM\sin45^{\circ}$,即$CM=\sqrt{2}BH$。
综上,(1)通过证明三角形全等得出邻边相等,进而证明矩形是正方形;(2)$FH=CF + AH$;(3)$CM=\sqrt{2}BH$。
查看更多完整答案,请扫码查看


