《2025年全效学习学业评价方案九年级数学上册北师大版》

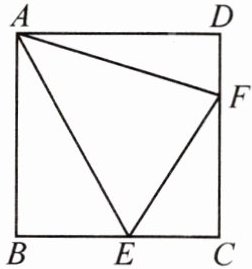
8. 如图，在$Rt\triangle CEF$中，$\angle C = 90^{\circ}$，$\angle CEF$，$\angle CFE$的外角平分线相交于点$A$，过点$A$分别作直线$CE$，$CF$的垂线，$B$，$D$为垂足.
(1)$\angle EAF=$45$^{\circ}$（直接写出结果不写解答过程）；
(2)①求证：四边形$ABCD$是正方形.
②若$BE = EC = 3$，求$DF$的长.

①证明：因为$AB\perp CE$，$AD\perp CF$，$\angle C = 90^{\circ}$，所以四边形$ABCD$是矩形。过点$A$作$AH\perp EF$于$H$。因为$AE$平分$\angle MEF$，$AB\perp CE$，$AH\perp EF$，所以$AB = AH$。同理$AD = AH$，所以$AB = AD$，故四边形$ABCD$是正方形。②解：因为四边形$ABCD$是正方形，$BE = EC = 3$，所以$BC=6$，$AB = AD = 6$。由角平分线性质知$BE = EH = 3$，设$DF=x$，则$FH = x$，$EF=3 + x$，$CF=6 - x$。在$Rt\triangle CEF$中，$3^{2}+(6 - x)^{2}=(3 + x)^{2}$，解得$x = 2$，即$DF=2$。

答案： 1. 求$\angle EAF$的度数：
在$Rt\triangle CEF$中，$\angle C = 90^{\circ}$，则$\angle CEF+\angle CFE = 90^{\circ}$。
设$\angle CEF$的外角为$\angle MEF$，$\angle CFE$的外角为$\angle NFE$，则$\angle MEF = 180^{\circ}-\angle CEF$，$\angle NFE = 180^{\circ}-\angle CFE$。
因为$AE$平分$\angle MEF$，$AF$平分$\angle NFE$，所以$\angle AEF=\frac{1}{2}\angle MEF=\frac{1}{2}(180^{\circ}-\angle CEF)=90^{\circ}-\frac{1}{2}\angle CEF$，$\angle AFE=\frac{1}{2}\angle NFE = 90^{\circ}-\frac{1}{2}\angle CFE$。
在$\triangle AEF$中，根据三角形内角和定理$\angle EAF = 180^{\circ}-(\angle AEF+\angle AFE)$。
把$\angle AEF = 90^{\circ}-\frac{1}{2}\angle CEF$，$\angle AFE = 90^{\circ}-\frac{1}{2}\angle CFE$代入可得：
$\angle EAF=180^{\circ}-(90^{\circ}-\frac{1}{2}\angle CEF + 90^{\circ}-\frac{1}{2}\angle CFE)$。
又因为$\angle CEF+\angle CFE = 90^{\circ}$，所以$\angle EAF = 45^{\circ}$。
2. ①证明四边形$ABCD$是正方形：
因为$AB\perp CE$，$AD\perp CF$，$\angle C = 90^{\circ}$，所以四边形$ABCD$是矩形（有三个角是直角的四边形是矩形）。
过点$A$作$AH\perp EF$于$H$。
因为$AE$平分$\angle MEF$，$AB\perp CE$，$AH\perp EF$，根据角平分线的性质：角平分线上的点到角两边的距离相等，所以$AB = AH$。
同理，因为$AF$平分$\angle NFE$，$AD\perp CF$，$AH\perp EF$，所以$AD = AH$。
所以$AB = AD$。
因为四边形$ABCD$是矩形且$AB = AD$，所以四边形$ABCD$是正方形（一组邻边相等的矩形是正方形）。
3. ②求$DF$的长：
因为四边形$ABCD$是正方形，所以$AB = BC = CD = AD$。
已知$BE = EC = 3$，则$BC=BE + EC=6$，所以$AB = AD = 6$。
因为$AE$平分$\angle MEF$，$AB\perp CE$，$AH\perp EF$，所以$BE = EH = 3$（角平分线性质）。
同理$DF = FH$。
设$DF=x$，则$FH = x$，$EF=EH + FH=3 + x$，$CF=CD - DF=6 - x$，$CE = 3$。
在$Rt\triangle CEF$中，根据勾股定理$CE^{2}+CF^{2}=EF^{2}$。
即$3^{2}+(6 - x)^{2}=(3 + x)^{2}$。
展开得$9+36-12x+x^{2}=9 + 6x+x^{2}$。
移项得$9+36-12x+x^{2}-9 - 6x - x^{2}=0$。
合并同类项得$36-18x = 0$。
移项得$18x = 36$，解得$x = 2$。
综上，（1）$\angle EAF = 45^{\circ}$；（2）①证明如上；②$DF = 2$。

9. [2024秋·锦江区校级月考]如图，在矩形$ABCD$中，$\angle BAD$的平分线交$BC$于点$E$，$EF\perp AD$于点$F$，$DG\perp AE$于点$G$，$DG$与$EF$交于点$O$.
(1)求证：四边形$ABEF$是正方形；
(2)若$AD = AE$，求证：$AB = AG$；
(3)在(2)的条件下，已知$AB = 1$，求$OF$的长.

答案： 1. （1）证明：
因为四边形$ABCD$是矩形，所以$\angle B=\angle BAD = 90^{\circ}$，$AF// BE$。
又因为$EF\perp AD$，所以$\angle AFE = 90^{\circ}$，则四边形$ABEF$是矩形。
因为$AE$平分$\angle BAD$，所以$\angle BAE=\angle FAE = 45^{\circ}$。
在$\triangle ABE$中，$\angle B = 90^{\circ}$，$\angle BAE = 45^{\circ}$，所以$\angle BEA=\angle BAE = 45^{\circ}$，则$AB = BE$。
因为矩形$ABEF$的邻边$AB = BE$，所以四边形$ABEF$是正方形。
2. （2）证明：
因为$AE$平分$\angle BAD$，所以$\angle DAG=\angle BAE = 45^{\circ}$。
因为$DG\perp AE$，所以$\angle AGD = 90^{\circ}$。
在$\triangle AGD$和$\triangle ABE$中：
$\angle AGD=\angle B = 90^{\circ}$，$\angle DAG=\angle BAE = 45^{\circ}$，$AD = AE$。
根据$AAS$（两角及其中一角的对边对应相等的两个三角形全等），可得$\triangle AGD\cong\triangle ABE$。
所以$AB = AG$。
3. （3）解：
因为$AB = 1$，由（2）知$AB = AG = 1$，且四边形$ABEF$是正方形，所以$AE=\sqrt{AB^{2}+BE^{2}}=\sqrt{1 + 1}=\sqrt{2}$（根据正方形边长相等$AB = BE$，利用勾股定理$a^{2}+b^{2}=c^{2}$，这里$a = b = AB$，$c = AE$）。
所以$GE=AE - AG=\sqrt{2}-1$。
因为$\angle FAE = 45^{\circ}$，$\angle AFE = 90^{\circ}$，所以$\angle FGE = 45^{\circ}$，$\angle FEG = 45^{\circ}$，则$FG = EF - EG$。
又因为$EF = AB = 1$，所以$FG = 1-(\sqrt{2}-1)=2 - \sqrt{2}$。
因为$\angle FDO=\angle FGE = 45^{\circ}$，$\angle DFO = 90^{\circ}$，所以$OF = FG$。
所以$OF = 2-\sqrt{2}$。
综上，（1）得证；（2）得证；（3）$OF$的长为$2 - \sqrt{2}$。