《2025年全效学习学业评价方案九年级数学上册北师大版》

1. 下列说法中，错误的是 （C）
A. 有一组邻边相等的平行四边形是菱形
B. 平行四边形对角相等
C. 对角线互相垂直且相等的四边形是矩形
D. 对角线互相垂直的矩形是正方形

答案： C

2. 若菱形的周长为20，两邻角的比为2:1，则一组对边的距离为 （D）
A. $\frac{\sqrt{3}}{2}$
B. $\frac{3\sqrt{3}}{2}$
C. $3\sqrt{3}$
D. $\frac{5\sqrt{3}}{2}$

答案： D

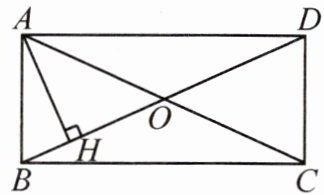
3. 如图，矩形$ABCD$的对角线$AC$，$BD$相交于点$O$，$AH\perp BD$于点$H$，$OH = 2BH$，$AH = 5$.
(1)求$BH$的长；
(2)求矩形$ABCD$的面积.

答案：
(1)$BH=\sqrt {5}$
(2)$30\sqrt {5}$

4. 如图，在$\triangle ABC$中，分别以$AB$，$AC$，$BC$为边在$BC$的同侧作等边三角形$ABD$，等边三角形$ACE$，等边三角形$BCF$.
(1)求证：四边形$DAEF$是平行四边形.
(2)探究下列问题（只填满足的条件，不需证明）：
①当$\triangle ABC$满足$\angle BAC = 150^{\circ}$时，四边形$DAEF$是矩形；
②当$\triangle ABC$满足$AB = AC\neq BC$时，四边形$DAEF$是菱形；
③当$\triangle ABC$满足$\angle BAC = 150^{\circ}$且$AB = AC\neq BC$时，四边形$DAEF$是正方形；
④当$\triangle ABC$满足$\angle BAC = 60^{\circ}$时，以$D$，$A$，$E$，$F$为顶点的四边形不存在.

答案： 1. （1）证明：
因为$\triangle ABD$和$\triangle FBC$都是等边三角形，
所以$BD = BA$，$BF = BC$，$\angle DBA=\angle FBC = 60^{\circ}$。
则$\angle DBA-\angle FBA=\angle FBC - \angle FBA$，即$\angle DBF=\angle ABC$。
在$\triangle DBF$和$\triangle ABC$中，$\begin{cases}BD = BA\\\angle DBF=\angle ABC\\BF = BC\end{cases}$，根据$SAS$（边角边）定理可得$\triangle DBF\cong\triangle ABC$。
所以$DF = AC$。
又因为$\triangle ACE$是等边三角形，所以$AC = AE$，则$DF = AE$。
同理，因为$\triangle ACE$和$\triangle FCB$都是等边三角形，
所以$CF = CB$，$CE = CA$，$\angle FCB=\angle ECA = 60^{\circ}$。
则$\angle FCB-\angle FCA=\angle ECA-\angle FCA$，即$\angle FCE=\angle BCA$。
在$\triangle FCE$和$\triangle BCA$中，$\begin{cases}CF = CB\\\angle FCE=\angle BCA\\CE = CA\end{cases}$，根据$SAS$定理可得$\triangle FCE\cong\triangle BCA$。
所以$EF = AB$。
又因为$\triangle ABD$是等边三角形，所以$AB = AD$，则$EF = AD$。
因为$DF = AE$，$EF = AD$，根据平行四边形的判定定理（两组对边分别相等的四边形是平行四边形），所以四边形$DAEF$是平行四边形。
2. （2）
①当$\angle BAC = 150^{\circ}$时：
因为四边形$DAEF$是平行四边形，$\angle DAE=360^{\circ}-\angle DAB-\angle BAC-\angle CAE$，$\angle DAB = 60^{\circ}$，$\angle CAE = 60^{\circ}$，当$\angle BAC = 150^{\circ}$时，$\angle DAE = 90^{\circ}$，根据矩形的判定定理（有一个角是直角的平行四边形是矩形），所以四边形$DAEF$是矩形。
②当$AB = AC\neq BC$时：
因为$AD = AB$，$AE = AC$，$AB = AC$，所以$AD = AE$，又因为四边形$DAEF$是平行四边形，根据菱形的判定定理（一组邻边相等的平行四边形是菱形），所以四边形$DAEF$是菱形（若$AB = AC = BC$，则$\triangle ABC$是等边三角形，此时$D$、$A$、$E$、$F$共线，四边形不存在）。
③当$\angle BAC = 150^{\circ}$且$AB = AC\neq BC$时：
由①知$\angle DAE = 90^{\circ}$，由②知$AD = AE$，又因为四边形$DAEF$是平行四边形，根据正方形的判定定理（有一个角是直角且一组邻边相等的平行四边形是正方形），所以四边形$DAEF$是正方形。
④当$\angle BAC = 60^{\circ}$时：
此时$\angle DAE=360^{\circ}-\angle DAB-\angle BAC-\angle CAE=360^{\circ}-60^{\circ}-60^{\circ}-60^{\circ}=180^{\circ}$，$D$、$A$、$E$共线，所以以$D$，$A$，$E$，$F$为顶点的四边形不存在。
综上，答案依次为：（1）证明过程如上述；（2）①$\angle BAC = 150^{\circ}$；②$AB = AC\neq BC$；③$\angle BAC = 150^{\circ}$且$AB = AC\neq BC$；④$\angle BAC = 60^{\circ}$。