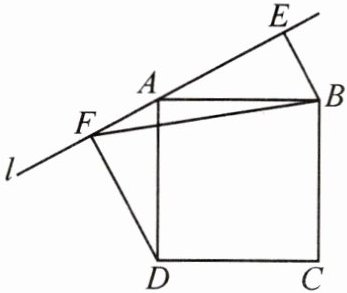
3. (内弦图模型)如图,正方形ABCD的顶点A在直线l上,分别过点B,D作直线l的垂线,垂足分别为E,F,连接BF.
(1)请找出一对全等的三角形,并说明理由;
(2)若$AE=6,AB=2\sqrt {13}$,求$\triangle ABF$的面积.
(1)请找出一对全等的三角形,并说明理由;
(2)若$AE=6,AB=2\sqrt {13}$,求$\triangle ABF$的面积.

答案:
1. (1)
解:$\triangle ABE\cong\triangle DAF$。
理由:
因为四边形$ABCD$是正方形,所以$AB = AD$,$\angle BAD=90^{\circ}$,则$\angle BAE+\angle DAF = 90^{\circ}$。
又因为$BE\perp l$,$DF\perp l$,所以$\angle AEB=\angle DFA = 90^{\circ}$,且$\angle BAE+\angle ABE = 90^{\circ}$。
所以$\angle ABE=\angle DAF$(同角的余角相等)。
在$\triangle ABE$和$\triangle DAF$中,$\left\{\begin{array}{l}\angle AEB=\angle DFA\\\angle ABE=\angle DAF\\AB = DA\end{array}\right.$。
根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ABE\cong\triangle DAF$。
2. (2)
解:在$Rt\triangle ABE$中,根据勾股定理$BE=\sqrt{AB^{2}-AE^{2}}$。
已知$AE = 6$,$AB = 2\sqrt{13}$,则$BE=\sqrt{(2\sqrt{13})^{2}-6^{2}}=\sqrt{52 - 36}=\sqrt{16}=4$。
因为$\triangle ABE\cong\triangle DAF$,所以$AF = BE = 4$。
根据三角形面积公式$S_{\triangle ABF}=\frac{1}{2}AF\cdot AE$。
把$AF = 4$,$AE = 6$代入可得$S_{\triangle ABF}=\frac{1}{2}×4×6 = 12$。
综上,(1)$\triangle ABE\cong\triangle DAF$(理由见上述过程);(2)$\triangle ABF$的面积为$12$。
解:$\triangle ABE\cong\triangle DAF$。
理由:
因为四边形$ABCD$是正方形,所以$AB = AD$,$\angle BAD=90^{\circ}$,则$\angle BAE+\angle DAF = 90^{\circ}$。
又因为$BE\perp l$,$DF\perp l$,所以$\angle AEB=\angle DFA = 90^{\circ}$,且$\angle BAE+\angle ABE = 90^{\circ}$。
所以$\angle ABE=\angle DAF$(同角的余角相等)。
在$\triangle ABE$和$\triangle DAF$中,$\left\{\begin{array}{l}\angle AEB=\angle DFA\\\angle ABE=\angle DAF\\AB = DA\end{array}\right.$。
根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ABE\cong\triangle DAF$。
2. (2)
解:在$Rt\triangle ABE$中,根据勾股定理$BE=\sqrt{AB^{2}-AE^{2}}$。
已知$AE = 6$,$AB = 2\sqrt{13}$,则$BE=\sqrt{(2\sqrt{13})^{2}-6^{2}}=\sqrt{52 - 36}=\sqrt{16}=4$。
因为$\triangle ABE\cong\triangle DAF$,所以$AF = BE = 4$。
根据三角形面积公式$S_{\triangle ABF}=\frac{1}{2}AF\cdot AE$。
把$AF = 4$,$AE = 6$代入可得$S_{\triangle ABF}=\frac{1}{2}×4×6 = 12$。
综上,(1)$\triangle ABE\cong\triangle DAF$(理由见上述过程);(2)$\triangle ABF$的面积为$12$。
4. (外弦图模型)如图,在正方形ABCD中,G是边BC上的任意一点(不与点B,C重合),$DE⊥AG$于点E,$BF// DE$,且交AG于点F.
(1)求证:$AF-BF=EF.$
(2)四边形BFDE有可能是平行四边形吗?若可能,请指出此时点G的位置;若不可能,请说明理由.

(1)求证:$AF-BF=EF.$
(2)四边形BFDE有可能是平行四边形吗?若可能,请指出此时点G的位置;若不可能,请说明理由.

答案:
1. (1)证明:
因为四边形$ABCD$是正方形,所以$AB = AD$,$\angle BAD=90^{\circ}$,即$\angle BAF+\angle DAE = 90^{\circ}$。
又因为$DE\perp AG$,所以$\angle AED = 90^{\circ}$,则$\angle ADE+\angle DAE = 90^{\circ}$。
所以$\angle BAF=\angle ADE$(同角的余角相等)。
因为$BF// DE$,$DE\perp AG$,所以$\angle BFA=\angle AED = 90^{\circ}$。
在$\triangle ABF$和$\triangle DAE$中:
$\left\{\begin{array}{l}\angle BFA=\angle AED\\\angle BAF=\angle ADE\\AB = DA\end{array}\right.$
根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ABF\cong\triangle DAE$。
所以$BF = AE$。
因为$AF - AE=EF$,将$BF = AE$代入可得$AF - BF=EF$。
2. (2)
若四边形$BFDE$是平行四边形,因为$BF// DE$,则需$BF = DE$。
由(1)知$\triangle ABF\cong\triangle DAE$,则$BF = AE$,若$BF = DE$,则$AE = DE$。
因为$\angle AED = 90^{\circ}$,所以$\angle DAE=\angle ADE = 45^{\circ}$。
又因为$\angle BAF=\angle ADE$,所以$\angle BAF = 45^{\circ}$。
在$Rt\triangle ABG$中,$\angle ABG = 90^{\circ}$,$\angle BAG = 45^{\circ}$,所以$\angle AGB=\angle BAG = 45^{\circ}$。
根据等角对等边,可得$AB = BG$。
所以当点$G$为$BC$中点时,四边形$BFDE$是平行四边形。
综上,(1)证明见上述过程;(2)当点$G$为$BC$中点时,四边形$BFDE$是平行四边形。
因为四边形$ABCD$是正方形,所以$AB = AD$,$\angle BAD=90^{\circ}$,即$\angle BAF+\angle DAE = 90^{\circ}$。
又因为$DE\perp AG$,所以$\angle AED = 90^{\circ}$,则$\angle ADE+\angle DAE = 90^{\circ}$。
所以$\angle BAF=\angle ADE$(同角的余角相等)。
因为$BF// DE$,$DE\perp AG$,所以$\angle BFA=\angle AED = 90^{\circ}$。
在$\triangle ABF$和$\triangle DAE$中:
$\left\{\begin{array}{l}\angle BFA=\angle AED\\\angle BAF=\angle ADE\\AB = DA\end{array}\right.$
根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ABF\cong\triangle DAE$。
所以$BF = AE$。
因为$AF - AE=EF$,将$BF = AE$代入可得$AF - BF=EF$。
2. (2)
若四边形$BFDE$是平行四边形,因为$BF// DE$,则需$BF = DE$。
由(1)知$\triangle ABF\cong\triangle DAE$,则$BF = AE$,若$BF = DE$,则$AE = DE$。
因为$\angle AED = 90^{\circ}$,所以$\angle DAE=\angle ADE = 45^{\circ}$。
又因为$\angle BAF=\angle ADE$,所以$\angle BAF = 45^{\circ}$。
在$Rt\triangle ABG$中,$\angle ABG = 90^{\circ}$,$\angle BAG = 45^{\circ}$,所以$\angle AGB=\angle BAG = 45^{\circ}$。
根据等角对等边,可得$AB = BG$。
所以当点$G$为$BC$中点时,四边形$BFDE$是平行四边形。
综上,(1)证明见上述过程;(2)当点$G$为$BC$中点时,四边形$BFDE$是平行四边形。
查看更多完整答案,请扫码查看


