5. 如图,点 E,F 在正方形 ABCD 的对角线 AC 上,∠EBF=45°。
(1)如图 1,当 BE=BF 时,求证:
①AE=CF;
②△AFB∽△CEB。
(2)如图 2,延长 BF 交 CD 于点 G,连接 EG。试判断线段 BE 与 EG 的关系,并说明理由。
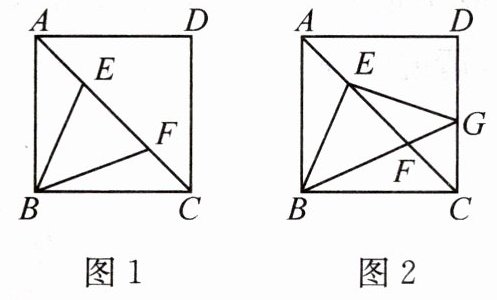
(1)如图 1,当 BE=BF 时,求证:
①AE=CF;
②△AFB∽△CEB。
(2)如图 2,延长 BF 交 CD 于点 G,连接 EG。试判断线段 BE 与 EG 的关系,并说明理由。

答案:
(1)①
证明:
因为四边形$ABCD$是正方形,所以$AB = BC$,$\angle BAC=\angle BCA = 45^{\circ}$。
又因为$BE = BF$,所以$\angle BEF=\angle BFE$。
而$\angle BEF=\angle BAC+\angle ABE$,$\angle BFE=\angle BCA+\angle CBF$,所以$\angle ABE=\angle CBF$。
在$\triangle ABE$和$\triangle CBF$中,$\begin{cases}AB = BC\\\angle BAE=\angle BCF = 45^{\circ}\\\angle ABE=\angle CBF\end{cases}$,根据$ASA$(角 - 边 - 角)定理,$\triangle ABE\cong\triangle CBF$。
所以$AE = CF$。
②
证明:因为$AE = CF$,所以$AE + EF=CF + EF$,即$AF = CE$。
又因为$BE = BF$,$\angle BAC=\angle BCA = 45^{\circ}$,所以$\frac{AF}{CE}=\frac{BF}{BE}=1$,$\angle BAF=\angle BCE = 45^{\circ}$。
根据两边对应成比例且夹角相等的两个三角形相似,可得$\triangle AFB\sim\triangle CEB$。
(2)
解:$BE = EG$,$BE\perp EG$。
理由:
延长$DC$到$H$,使$CH = AE$,连接$BH$。
因为四边形$ABCD$是正方形,所以$AB = BC$,$\angle BAE=\angle BCH = 90^{\circ}$。
在$\triangle ABE$和$\triangle CBH$中,$\begin{cases}AB = BC\\\angle BAE=\angle BCH\\AE = CH\end{cases}$,根据$SAS$(边 - 角 - 边)定理,$\triangle ABE\cong\triangle CBH$。
所以$BE = BH$,$\angle ABE=\angle CBH$。
因为$\angle ABC = 90^{\circ}$,$\angle EBF = 45^{\circ}$,所以$\angle ABE+\angle CBF = 45^{\circ}$,则$\angle CBH+\angle CBF = 45^{\circ}$,即$\angle HBF=\angle EBF = 45^{\circ}$。
在$\triangle EBF$和$\triangle HBF$中,$\begin{cases}BE = BH\\\angle EBF=\angle HBF\\BF = BF\end{cases}$,根据$SAS$定理,$\triangle EBF\cong\triangle HBF$。
所以$EF = FH$,$\angle BEF=\angle BHF$。
因为$\triangle ABE\cong\triangle CBH$,所以$\angle AEB=\angle BHC$。
又因为$\angle BHC+\angle BHG = 180^{\circ}$,$\angle BEF+\angle BEG = 180^{\circ}$,所以$\angle BEG=\angle BHG$。
在$\triangle BCG$中,$\angle BCG = 90^{\circ}$,$\angle GBC+\angle BGC = 90^{\circ}$。
因为$\triangle EBF\cong\triangle HBF$,所以$\angle BFE=\angle BFH$。
又因为$\angle BFC+\angle BFH = 180^{\circ}$,$\angle BFC=\angle BFG+\angle GFC$,$\angle BAE = 45^{\circ}$,$\angle BCH = 90^{\circ}$,$\angle DCF = 45^{\circ}$,$\angle BGF+\angle GFC+\angle FCG = 180^{\circ}$,$\angle FCG = 45^{\circ}$。
可得$\angle BEG = 90^{\circ}$。
因为$\triangle EBF\cong\triangle HBF$,$EF = FH$,$CH = AE$,$\angle ECG = 45^{\circ}$,$\angle BAE = 45^{\circ}$,$\triangle ABE\cong\triangle CBH$,通过角度和边的关系可证$\triangle BEG$是等腰直角三角形。
所以$BE = EG$,$BE\perp EG$。
综上,(1)①得证$AE = CF$;②得证$\triangle AFB\sim\triangle CEB$;(2)$BE = EG$且$BE\perp EG$。
证明:
因为四边形$ABCD$是正方形,所以$AB = BC$,$\angle BAC=\angle BCA = 45^{\circ}$。
又因为$BE = BF$,所以$\angle BEF=\angle BFE$。
而$\angle BEF=\angle BAC+\angle ABE$,$\angle BFE=\angle BCA+\angle CBF$,所以$\angle ABE=\angle CBF$。
在$\triangle ABE$和$\triangle CBF$中,$\begin{cases}AB = BC\\\angle BAE=\angle BCF = 45^{\circ}\\\angle ABE=\angle CBF\end{cases}$,根据$ASA$(角 - 边 - 角)定理,$\triangle ABE\cong\triangle CBF$。
所以$AE = CF$。
②
证明:因为$AE = CF$,所以$AE + EF=CF + EF$,即$AF = CE$。
又因为$BE = BF$,$\angle BAC=\angle BCA = 45^{\circ}$,所以$\frac{AF}{CE}=\frac{BF}{BE}=1$,$\angle BAF=\angle BCE = 45^{\circ}$。
根据两边对应成比例且夹角相等的两个三角形相似,可得$\triangle AFB\sim\triangle CEB$。
(2)
解:$BE = EG$,$BE\perp EG$。
理由:
延长$DC$到$H$,使$CH = AE$,连接$BH$。
因为四边形$ABCD$是正方形,所以$AB = BC$,$\angle BAE=\angle BCH = 90^{\circ}$。
在$\triangle ABE$和$\triangle CBH$中,$\begin{cases}AB = BC\\\angle BAE=\angle BCH\\AE = CH\end{cases}$,根据$SAS$(边 - 角 - 边)定理,$\triangle ABE\cong\triangle CBH$。
所以$BE = BH$,$\angle ABE=\angle CBH$。
因为$\angle ABC = 90^{\circ}$,$\angle EBF = 45^{\circ}$,所以$\angle ABE+\angle CBF = 45^{\circ}$,则$\angle CBH+\angle CBF = 45^{\circ}$,即$\angle HBF=\angle EBF = 45^{\circ}$。
在$\triangle EBF$和$\triangle HBF$中,$\begin{cases}BE = BH\\\angle EBF=\angle HBF\\BF = BF\end{cases}$,根据$SAS$定理,$\triangle EBF\cong\triangle HBF$。
所以$EF = FH$,$\angle BEF=\angle BHF$。
因为$\triangle ABE\cong\triangle CBH$,所以$\angle AEB=\angle BHC$。
又因为$\angle BHC+\angle BHG = 180^{\circ}$,$\angle BEF+\angle BEG = 180^{\circ}$,所以$\angle BEG=\angle BHG$。
在$\triangle BCG$中,$\angle BCG = 90^{\circ}$,$\angle GBC+\angle BGC = 90^{\circ}$。
因为$\triangle EBF\cong\triangle HBF$,所以$\angle BFE=\angle BFH$。
又因为$\angle BFC+\angle BFH = 180^{\circ}$,$\angle BFC=\angle BFG+\angle GFC$,$\angle BAE = 45^{\circ}$,$\angle BCH = 90^{\circ}$,$\angle DCF = 45^{\circ}$,$\angle BGF+\angle GFC+\angle FCG = 180^{\circ}$,$\angle FCG = 45^{\circ}$。
可得$\angle BEG = 90^{\circ}$。
因为$\triangle EBF\cong\triangle HBF$,$EF = FH$,$CH = AE$,$\angle ECG = 45^{\circ}$,$\angle BAE = 45^{\circ}$,$\triangle ABE\cong\triangle CBH$,通过角度和边的关系可证$\triangle BEG$是等腰直角三角形。
所以$BE = EG$,$BE\perp EG$。
综上,(1)①得证$AE = CF$;②得证$\triangle AFB\sim\triangle CEB$;(2)$BE = EG$且$BE\perp EG$。
6. 如图,在 Rt△ABC 中,AC=BC,∠ACB=90°,点 D,E 分别在 AC,BC 上,且 CD=CE。
(1)求证:∠CAE=∠CBD;
(2)若 F,G 分别是 BD,AE 的中点,连接 CF,CG,FG,CF 交 AE 于点 H,AC=2√2,CE=1,求△CGF 的面积。

(1)求证:∠CAE=∠CBD;
(2)若 F,G 分别是 BD,AE 的中点,连接 CF,CG,FG,CF 交 AE 于点 H,AC=2√2,CE=1,求△CGF 的面积。

答案:
1. (1)证明:
在$Rt\triangle ACE$和$Rt\triangle BCD$中:
已知$AC = BC$,$\angle ACB=\angle ACE = \angle BCD = 90^{\circ}$,$CD = CE$。
根据$SAS$(边角边)判定定理,$\triangle ACE\cong\triangle BCD$。
因为全等三角形的对应角相等,所以$\angle CAE=\angle CBD$。
2. (2)
首先,计算$AE$的长度:
已知$AC = 2\sqrt{2}$,$CE = 1$,在$Rt\triangle ACE$中,根据勾股定理$a^{2}+b^{2}=c^{2}$(这里$a = CE$,$b = AC$,$c = AE$),则$AE=\sqrt{AC^{2}+CE^{2}}=\sqrt{(2\sqrt{2})^{2}+1^{2}}=\sqrt{8 + 1}=3$。
同理,在$Rt\triangle BCD$中,$BC = AC = 2\sqrt{2}$,$CD = CE = 1$,$BD=\sqrt{BC^{2}+CD^{2}}=\sqrt{(2\sqrt{2})^{2}+1^{2}} = 3$。
然后,因为$\triangle ACE\cong\triangle BCD$,$F$是$BD$中点,$G$是$AE$中点:
根据直角三角形斜边中线定理:直角三角形斜边的中线等于斜边的一半。在$Rt\triangle BCD$中,$CF=\frac{1}{2}BD$;在$Rt\triangle ACE$中,$CG=\frac{1}{2}AE$。
所以$CF = CG=\frac{3}{2}$。
又因为$\angle CAE=\angle CBD$,$\angle AHC=\angle BHF$,$\angle ACB = 90^{\circ}$,所以$\angle FCG = 90^{\circ}$。
最后,计算$\triangle CGF$的面积:
根据三角形面积公式$S=\frac{1}{2}ab$(这里$a = CF$,$b = CG$,且$\angle FCG = 90^{\circ}$)。
则$S_{\triangle CGF}=\frac{1}{2}×\frac{3}{2}×\frac{3}{2}=\frac{9}{8}$。
综上,(1)得证;(2)$\triangle CGF$的面积为$\frac{9}{8}$。
在$Rt\triangle ACE$和$Rt\triangle BCD$中:
已知$AC = BC$,$\angle ACB=\angle ACE = \angle BCD = 90^{\circ}$,$CD = CE$。
根据$SAS$(边角边)判定定理,$\triangle ACE\cong\triangle BCD$。
因为全等三角形的对应角相等,所以$\angle CAE=\angle CBD$。
2. (2)
首先,计算$AE$的长度:
已知$AC = 2\sqrt{2}$,$CE = 1$,在$Rt\triangle ACE$中,根据勾股定理$a^{2}+b^{2}=c^{2}$(这里$a = CE$,$b = AC$,$c = AE$),则$AE=\sqrt{AC^{2}+CE^{2}}=\sqrt{(2\sqrt{2})^{2}+1^{2}}=\sqrt{8 + 1}=3$。
同理,在$Rt\triangle BCD$中,$BC = AC = 2\sqrt{2}$,$CD = CE = 1$,$BD=\sqrt{BC^{2}+CD^{2}}=\sqrt{(2\sqrt{2})^{2}+1^{2}} = 3$。
然后,因为$\triangle ACE\cong\triangle BCD$,$F$是$BD$中点,$G$是$AE$中点:
根据直角三角形斜边中线定理:直角三角形斜边的中线等于斜边的一半。在$Rt\triangle BCD$中,$CF=\frac{1}{2}BD$;在$Rt\triangle ACE$中,$CG=\frac{1}{2}AE$。
所以$CF = CG=\frac{3}{2}$。
又因为$\angle CAE=\angle CBD$,$\angle AHC=\angle BHF$,$\angle ACB = 90^{\circ}$,所以$\angle FCG = 90^{\circ}$。
最后,计算$\triangle CGF$的面积:
根据三角形面积公式$S=\frac{1}{2}ab$(这里$a = CF$,$b = CG$,且$\angle FCG = 90^{\circ}$)。
则$S_{\triangle CGF}=\frac{1}{2}×\frac{3}{2}×\frac{3}{2}=\frac{9}{8}$。
综上,(1)得证;(2)$\triangle CGF$的面积为$\frac{9}{8}$。
查看更多完整答案,请扫码查看


