1. [2023秋·康平县期末]“保护生态环境,建设美好家园”是学校开展环保类社团活动的宗旨.为了解某校全体学生参加该学校五个环保类社团项目的意愿,随机抽取了40名学生进行问卷调查,每人只能从中选择一个项目,现将问卷调查结果绘制成不完整的统计图表:
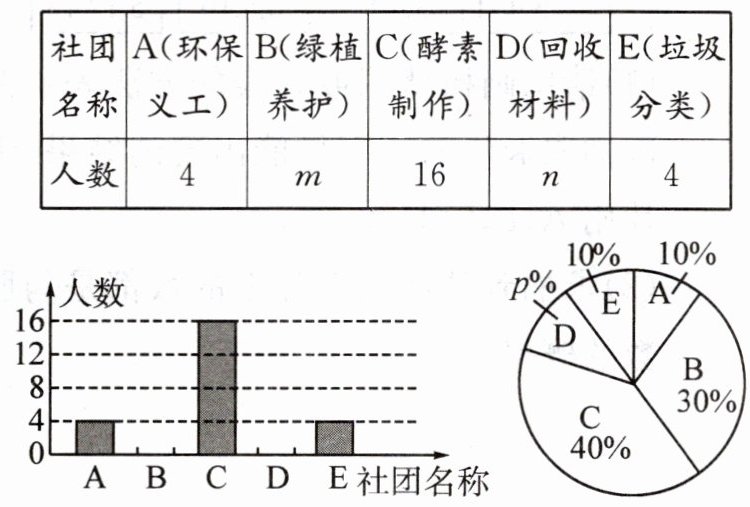
请你根据以上信息解答下列问题:
(1)填空:m=
(2)请用画树状图或列表法求随机抽取该校两名同学选择同一环保类社团项目的概率.

请你根据以上信息解答下列问题:
(1)填空:m=
12
;n=4
;p=10
;扇形统计图中D(回收材料)部分扇形的圆心角为36
°.(2)请用画树状图或列表法求随机抽取该校两名同学选择同一环保类社团项目的概率.
$\frac{1}{5}$
答案:
(1)12 4 10 36
(2)$\frac{1}{5}$
(1)12 4 10 36
(2)$\frac{1}{5}$
2. [2023秋·沈阳期中]李老师为了了解所教班级学生完成数学课前预习的具体情况,对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A.很好;B.较好;C.一般;D.不合格.并将调查结果绘制成以下两幅不完整的统计图.
请你根据统计图解答下列问题:
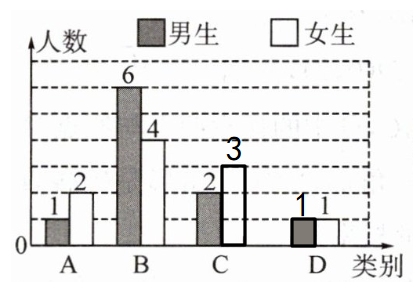
(1)请计算出C类女生的人数和D类男生的人数,并将条形统计图补充完整;
(2)为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树状图法求出所选的两位同学恰好是两位男同学的概率.
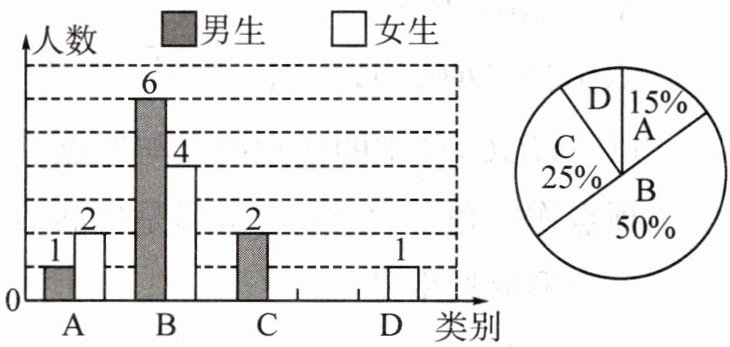
请你根据统计图解答下列问题:
(1)请计算出C类女生的人数和D类男生的人数,并将条形统计图补充完整;
(2)为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树状图法求出所选的两位同学恰好是两位男同学的概率.

答案:
(1)
首先,计算总人数:
已知$B$类人数为$6 + 4=10$人,$B$类占比$50\%$,设总人数为$x$,根据公式$\frac{10}{x}=50\%$(即$\frac{10}{x}=\frac{1}{2}$),可得$x = 20$人。
因为$C$类占比$25\%$,所以$C$类人数为$20×25\%=5$人,已知$C$类男生$2$人,那么$C$类女生人数为$5 - 2=3$人。
又因为$A$类占比$15\%$,所以$A$类人数为$20×15\% = 3$人,$D$类人数为$20-(3 + 10+5)=2$人,已知$D$类女生$1$人,所以$D$类男生人数为$2 - 1=1$人。
(2)
$A$类学生:$A$类有$3$人,其中男生$1$人,女生$2$人;$D$类学生:$D$类有$2$人,其中男生$1$人,女生$1$人。
画树状图:
设$A$类男生为$M_1$,$A$类女生为$F_1,F_2$;$D$类男生为$M_2$,$D$类女生为$F_3$。
树状图的第一层:从$A$类选,有$M_1,F_1,F_2$三种情况。
若从$A$类选$M_1$,第二层从$D$类选有$M_2,F_3$两种情况;若从$A$类选$F_1$,第二层从$D$类选有$M_2,F_3$两种情况;若从$A$类选$F_2$,第二层从$D$类选有$M_2,F_3$两种情况。
总共的情况数$n = 3×2=6$种。
所选两位同学恰好是两位男同学的情况只有$1$种($M_1$和$M_2$)。
根据概率公式$P=\frac{m}{n}$($m$是所求事件发生的情况数,$n$是总情况数),所以$P=\frac{1}{6}$。
综上,(1)$C$类女生人数为$3$人,$D$类男生人数为$1$人;(2)所选的两位同学恰好是两位男同学的概率为$\frac{1}{6}$。
(1)
首先,计算总人数:
已知$B$类人数为$6 + 4=10$人,$B$类占比$50\%$,设总人数为$x$,根据公式$\frac{10}{x}=50\%$(即$\frac{10}{x}=\frac{1}{2}$),可得$x = 20$人。
因为$C$类占比$25\%$,所以$C$类人数为$20×25\%=5$人,已知$C$类男生$2$人,那么$C$类女生人数为$5 - 2=3$人。
又因为$A$类占比$15\%$,所以$A$类人数为$20×15\% = 3$人,$D$类人数为$20-(3 + 10+5)=2$人,已知$D$类女生$1$人,所以$D$类男生人数为$2 - 1=1$人。

(2)
$A$类学生:$A$类有$3$人,其中男生$1$人,女生$2$人;$D$类学生:$D$类有$2$人,其中男生$1$人,女生$1$人。
画树状图:
设$A$类男生为$M_1$,$A$类女生为$F_1,F_2$;$D$类男生为$M_2$,$D$类女生为$F_3$。
树状图的第一层:从$A$类选,有$M_1,F_1,F_2$三种情况。
若从$A$类选$M_1$,第二层从$D$类选有$M_2,F_3$两种情况;若从$A$类选$F_1$,第二层从$D$类选有$M_2,F_3$两种情况;若从$A$类选$F_2$,第二层从$D$类选有$M_2,F_3$两种情况。
总共的情况数$n = 3×2=6$种。
所选两位同学恰好是两位男同学的情况只有$1$种($M_1$和$M_2$)。
根据概率公式$P=\frac{m}{n}$($m$是所求事件发生的情况数,$n$是总情况数),所以$P=\frac{1}{6}$。
综上,(1)$C$类女生人数为$3$人,$D$类男生人数为$1$人;(2)所选的两位同学恰好是两位男同学的概率为$\frac{1}{6}$。
查看更多完整答案,请扫码查看


