5. 如图,在菱形$ABCD$中,对角线$AC$,$BD$相交于点$O$,$DE// AC$,$AE// BD$.
(1)求证:四边形$AODE$是矩形;
(2)连接$CE$,若$AB = 2\sqrt{3}$,$\angle BCD = 120^{\circ}$,求$CE$的长.

(1)求证:四边形$AODE$是矩形;
(2)连接$CE$,若$AB = 2\sqrt{3}$,$\angle BCD = 120^{\circ}$,求$CE$的长.

答案:
1. (1)证明:
因为$DE// AC$,$AE// BD$,
根据平行四边形的判定定理(两组对边分别平行的四边形是平行四边形),所以四边形$AODE$是平行四边形。
又因为四边形$ABCD$是菱形,根据菱形的性质(菱形的对角线互相垂直),所以$AC\perp BD$,即$\angle AOD = 90^{\circ}$。
再根据矩形的判定定理(有一个角是直角的平行四边形是矩形),所以平行四边形$AODE$是矩形。
2. (2)解:
因为四边形$ABCD$是菱形,$AB = 2\sqrt{3}$,所以$AB=BC = CD = DA=2\sqrt{3}$。
因为$\angle BCD = 120^{\circ}$,$AB// CD$,所以$\angle ABC=60^{\circ}$。
所以$\triangle ABC$是等边三角形(有一个角是$60^{\circ}$的等腰三角形是等边三角形),则$AC = AB = 2\sqrt{3}$。
因为四边形$ABCD$是菱形,所以$AC\perp BD$,$OA=\frac{1}{2}AC=\sqrt{3}$,$OB = OD$。
在$Rt\triangle AOB$中,根据勾股定理$a^{2}+b^{2}=c^{2}$(这里$c = AB = 2\sqrt{3}$,$a = OA=\sqrt{3}$),则$OB=\sqrt{AB^{2}-OA^{2}}=\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}=\sqrt{12 - 3}=3$,所以$OD = 3$。
因为四边形$AODE$是矩形,所以$AE = OD = 3$,$DE = OA=\sqrt{3}$,$\angle EAC = 90^{\circ}$。
在$Rt\triangle AEC$中,$AC = 2\sqrt{3}$,$AE = 3$,根据勾股定理$CE=\sqrt{AE^{2}+AC^{2}}$。
把$AE = 3$,$AC = 2\sqrt{3}$代入可得:$CE=\sqrt{3^{2}+(2\sqrt{3})^{2}}=\sqrt{9 + 12}=\sqrt{21}$。
综上,(1)得证;(2)$CE$的长为$\sqrt{21}$。
因为$DE// AC$,$AE// BD$,
根据平行四边形的判定定理(两组对边分别平行的四边形是平行四边形),所以四边形$AODE$是平行四边形。
又因为四边形$ABCD$是菱形,根据菱形的性质(菱形的对角线互相垂直),所以$AC\perp BD$,即$\angle AOD = 90^{\circ}$。
再根据矩形的判定定理(有一个角是直角的平行四边形是矩形),所以平行四边形$AODE$是矩形。
2. (2)解:
因为四边形$ABCD$是菱形,$AB = 2\sqrt{3}$,所以$AB=BC = CD = DA=2\sqrt{3}$。
因为$\angle BCD = 120^{\circ}$,$AB// CD$,所以$\angle ABC=60^{\circ}$。
所以$\triangle ABC$是等边三角形(有一个角是$60^{\circ}$的等腰三角形是等边三角形),则$AC = AB = 2\sqrt{3}$。
因为四边形$ABCD$是菱形,所以$AC\perp BD$,$OA=\frac{1}{2}AC=\sqrt{3}$,$OB = OD$。
在$Rt\triangle AOB$中,根据勾股定理$a^{2}+b^{2}=c^{2}$(这里$c = AB = 2\sqrt{3}$,$a = OA=\sqrt{3}$),则$OB=\sqrt{AB^{2}-OA^{2}}=\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}=\sqrt{12 - 3}=3$,所以$OD = 3$。
因为四边形$AODE$是矩形,所以$AE = OD = 3$,$DE = OA=\sqrt{3}$,$\angle EAC = 90^{\circ}$。
在$Rt\triangle AEC$中,$AC = 2\sqrt{3}$,$AE = 3$,根据勾股定理$CE=\sqrt{AE^{2}+AC^{2}}$。
把$AE = 3$,$AC = 2\sqrt{3}$代入可得:$CE=\sqrt{3^{2}+(2\sqrt{3})^{2}}=\sqrt{9 + 12}=\sqrt{21}$。
综上,(1)得证;(2)$CE$的长为$\sqrt{21}$。
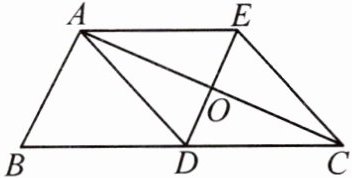
6. 如图,在$Rt\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AC = 2AB$,$AD$是$BC$边上的中线,过点$A$作$AE// BC$,过点$D$作$DE// AB$与$AC$,$AE$分别交于点$O$,$E$,连接$EC$.
(1)求证:四边形$ADCE$为菱形;
(2)设$OD = a$,求菱形$ADCE$的周长.
(1)求证:四边形$ADCE$为菱形;
(2)设$OD = a$,求菱形$ADCE$的周长.

答案:
1. (1)证明:
因为$AE// BC$,$DE// AB$,所以四边形$ABDE$是平行四边形。
则$AE = BD$。
在$Rt\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AD$是$BC$边上的中线,根据直角三角形斜边中线定理$AD = BD = CD$。
又因为$AE = BD$,所以$AE = CD$,且$AE// CD$。
所以四边形$ADCE$是平行四边形。
又因为$AD = CD$,根据菱形的判定定理(一组邻边相等的平行四边形是菱形),所以平行四边形$ADCE$是菱形。
2. (2)解:
因为四边形$ADCE$是菱形,所以$AC\perp DE$,$AO = CO$,$DO = EO$。
因为$DE// AB$,所以$\angle AOD=\angle BAC = 90^{\circ}$,$\triangle AOD\sim\triangle CAB$。
因为$AD$是$BC$边上的中线,所以$AB = 2OD$(由$\triangle AOD\sim\triangle CAB$,相似比$\frac{OD}{AB}=\frac{1}{2}$,因为$AC = 2AB$,$AO=\frac{1}{2}AC$)。
已知$OD = a$,则$AB = 2a$,$AC = 2AB = 4a$。
在$Rt\triangle AOD$中,根据勾股定理$AD=\sqrt{AO^{2}+OD^{2}}$,因为$AO=\frac{1}{2}AC = 2a$,$OD = a$,所以$AD=\sqrt{(2a)^{2}+a^{2}}=\sqrt{4a^{2}+a^{2}}=\sqrt{5a^{2}}=\sqrt{5}a$。
菱形$ADCE$的周长$C = 4AD$。
所以$C = 4\sqrt{5}a$。
综上,(1)证明如上;(2)菱形$ADCE$的周长为$4\sqrt{5}a$。
因为$AE// BC$,$DE// AB$,所以四边形$ABDE$是平行四边形。
则$AE = BD$。
在$Rt\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AD$是$BC$边上的中线,根据直角三角形斜边中线定理$AD = BD = CD$。
又因为$AE = BD$,所以$AE = CD$,且$AE// CD$。
所以四边形$ADCE$是平行四边形。
又因为$AD = CD$,根据菱形的判定定理(一组邻边相等的平行四边形是菱形),所以平行四边形$ADCE$是菱形。
2. (2)解:
因为四边形$ADCE$是菱形,所以$AC\perp DE$,$AO = CO$,$DO = EO$。
因为$DE// AB$,所以$\angle AOD=\angle BAC = 90^{\circ}$,$\triangle AOD\sim\triangle CAB$。
因为$AD$是$BC$边上的中线,所以$AB = 2OD$(由$\triangle AOD\sim\triangle CAB$,相似比$\frac{OD}{AB}=\frac{1}{2}$,因为$AC = 2AB$,$AO=\frac{1}{2}AC$)。
已知$OD = a$,则$AB = 2a$,$AC = 2AB = 4a$。
在$Rt\triangle AOD$中,根据勾股定理$AD=\sqrt{AO^{2}+OD^{2}}$,因为$AO=\frac{1}{2}AC = 2a$,$OD = a$,所以$AD=\sqrt{(2a)^{2}+a^{2}}=\sqrt{4a^{2}+a^{2}}=\sqrt{5a^{2}}=\sqrt{5}a$。
菱形$ADCE$的周长$C = 4AD$。
所以$C = 4\sqrt{5}a$。
综上,(1)证明如上;(2)菱形$ADCE$的周长为$4\sqrt{5}a$。
7. 如图,在$□ ABCD$中,$BC = 2AB$,$AB\perp AC$,分别在边$BC$,$AD$上的点$E$,$F$关于$AC$对称,$AC$与$EF$相交于点$O$,连接$AE$,$CF$,$DE$.
(1)试判断四边形$AECF$的形状,并说明理由;
(2)求证:$AE\perp DE$.

(1)试判断四边形$AECF$的形状,并说明理由;
(2)求证:$AE\perp DE$.

答案:
1. (1)
解:四边形$AECF$是菱形。
理由:
因为四边形$ABCD$是平行四边形,所以$AD// BC$,则$\angle FAO=\angle ECO$。
又因为点$E$,$F$关于$AC$对称,所以$AO = CO$,$EF\perp AC$,$\angle AOF=\angle COE = 90^{\circ}$。
在$\triangle AOF$和$\triangle COE$中,$\left\{\begin{array}{l}\angle FAO=\angle ECO\\AO = CO\\\angle AOF=\angle COE\end{array}\right.$,根据$ASA$(角 - 边 - 角)定理可得$\triangle AOF\cong\triangle COE$。
所以$AF = CE$。
又因为$AF// CE$,所以四边形$AECF$是平行四边形。
又因为$EF\perp AC$,根据“对角线互相垂直的平行四边形是菱形”,所以平行四边形$AECF$是菱形。
2. (2)
证明:
设$AB = x$,因为$BC = 2AB$,所以$BC = 2x$。
在$Rt\triangle ABC$中,$AB\perp AC$,根据勾股定理$AC=\sqrt{BC^{2}-AB^{2}}$,将$BC = 2x$,$AB = x$代入可得$AC=\sqrt{(2x)^{2}-x^{2}}=\sqrt{4x^{2}-x^{2}}=\sqrt{3x^{2}}=\sqrt{3}x$。
因为四边形$AECF$是菱形,所以$AE = CE$。
又因为$BC = 2AB$,$AB\perp AC$,$\angle ACB = 30^{\circ}$(在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于$30^{\circ}$,这里$AB=\frac{1}{2}BC$),所以$\angle B = 60^{\circ}$。
因为$AE = BE$($AE = CE$,$BC = 2AB$,$AB = BE$),所以$\triangle ABE$是等边三角形,则$AE = AB$,$\angle AEB = 60^{\circ}$,所以$\angle AEC = 120^{\circ}$。
因为四边形$ABCD$是平行四边形,$AD = BC$,$AD// BC$,$AB = CD$,又$AE = AB$,所以$AE = CD$。
因为$CE = AE$,$BC = 2AB$,所以$BE = AB = AE$,$CE = AB$,$AD = 2AB$,$AF = CE$,所以$FD = AB$,即$AE = FD$。
又因为$AD// BC$,所以$\angle DCE=\angle ADC$。
在$\triangle ADE$和$\triangle DCE$中,$\left\{\begin{array}{l}AE = CD\\\angle AED=\angle DCE\\ED = DE\end{array}\right.$($SAS$:边角边,$\angle AED = 180^{\circ}-\angle AEB=120^{\circ}$,$\angle DCE = 180^{\circ}-\angle BCD$,$\angle BCD = 60^{\circ}$,$\angle DCE = 120^{\circ}$)。
所以$\triangle ADE\cong\triangle DCE$,则$\angle ADE=\angle CDE$。
因为$AD// BC$,$\angle AEB = 60^{\circ}$,所以$\angle EAD=\angle AEB = 60^{\circ}$。
又因为$AD = 2AB$,$AE = AB$,所以$AD = 2AE$。
在$\triangle ADE$中,设$AE = a$,$AD = 2a$,过$E$作$EH\perp AD$于$H$。
因为$\angle EAH = 60^{\circ}$,$\angle AHE = 90^{\circ}$,所以$\angle AEH = 30^{\circ}$,则$AH=\frac{1}{2}AE=\frac{1}{2}a$,$EH=\sqrt{AE^{2}-AH^{2}}=\sqrt{a^{2}-\left(\frac{1}{2}a\right)^{2}}=\frac{\sqrt{3}}{2}a$,$HD=AD - AH=2a-\frac{1}{2}a=\frac{3}{2}a$。
根据勾股定理$DE=\sqrt{EH^{2}+HD^{2}}=\sqrt{\left(\frac{\sqrt{3}}{2}a\right)^{2}+\left(\frac{3}{2}a\right)^{2}}=\sqrt{\frac{3}{4}a^{2}+\frac{9}{4}a^{2}}=\sqrt{3}a$。
再根据勾股定理逆定理,$AE^{2}+DE^{2}=a^{2}+3a^{2}=4a^{2}$,$AD^{2}=(2a)^{2}=4a^{2}$。
所以$AE^{2}+DE^{2}=AD^{2}$,根据勾股定理逆定理可得$\angle AED = 90^{\circ}$,即$AE\perp DE$。
另一种方法:
(2)证明:
因为四边形$AECF$是菱形,所以$AE = CE$,$\angle EAC=\angle ECA$。
因为四边形$ABCD$是平行四边形,$AD = BC$,$AD// BC$,$AB = CD$。
设$AB = x$,则$BC = 2x$,在$Rt\triangle ABC$中,$\angle B = 60^{\circ}$,$\angle ACB = 30^{\circ}$。
因为$AE = BE$($AE = CE$,$BC = 2AB$),所以$\triangle ABE$是等边三角形,$AE = AB$,$\angle BAE = 60^{\circ}$。
因为$AD// BC$,所以$\angle EAD=\angle AEB = 60^{\circ}$,$AD = 2AB$,$AE = AB$,所以$AD = 2AE$。
连接$AC$,$BD$交于点$O$(平行四边形对角线互相平分),因为$AB\perp AC$,$O$是$BD$中点,$E$是$BC$中点($AE = CE$),所以$OE// CD$,$OE=\frac{1}{2}CD$(三角形中位线定理)。
又因为$AE = AB = CD$,$AD = 2AB$,$\overrightarrow{DE}=\overrightarrow{DC}+\overrightarrow{CE}$,$\overrightarrow{AE}=\overrightarrow{AB}$。
因为$\angle DAB = 120^{\circ}$($\angle B = 60^{\circ}$,$AD// BC$),$\vert\overrightarrow{AD}\vert = 2\vert\overrightarrow{AE}\vert$,$\vert\overrightarrow{AE}\vert=\vert\overrightarrow{CD}\vert$。
根据向量数量积公式$\overrightarrow{AE}\cdot\overrightarrow{DE}=\overrightarrow{AE}\cdot(\overrightarrow{DC}+\overrightarrow{CE})$,因为$\overrightarrow{AE}=\overrightarrow{DC}$,$\overrightarrow{CE}=-\overrightarrow{AE}$($AE = CE$,方向相反)。
$\overrightarrow{AE}\cdot\overrightarrow{DE}=\overrightarrow{AE}\cdot\overrightarrow{DC}+\overrightarrow{AE}\cdot\overrightarrow{CE}=\vert\overrightarrow{AE}\vert^{2}-\vert\overrightarrow{AE}\vert^{2}=0$。
因为$\overrightarrow{AE}\cdot\overrightarrow{DE} = 0$,所以$\overrightarrow{AE}\perp\overrightarrow{DE}$,即$AE\perp DE$。
综上,(1)四边形$AECF$是菱形;(2)$AE\perp DE$得证。
解:四边形$AECF$是菱形。
理由:
因为四边形$ABCD$是平行四边形,所以$AD// BC$,则$\angle FAO=\angle ECO$。
又因为点$E$,$F$关于$AC$对称,所以$AO = CO$,$EF\perp AC$,$\angle AOF=\angle COE = 90^{\circ}$。
在$\triangle AOF$和$\triangle COE$中,$\left\{\begin{array}{l}\angle FAO=\angle ECO\\AO = CO\\\angle AOF=\angle COE\end{array}\right.$,根据$ASA$(角 - 边 - 角)定理可得$\triangle AOF\cong\triangle COE$。
所以$AF = CE$。
又因为$AF// CE$,所以四边形$AECF$是平行四边形。
又因为$EF\perp AC$,根据“对角线互相垂直的平行四边形是菱形”,所以平行四边形$AECF$是菱形。
2. (2)
证明:
设$AB = x$,因为$BC = 2AB$,所以$BC = 2x$。
在$Rt\triangle ABC$中,$AB\perp AC$,根据勾股定理$AC=\sqrt{BC^{2}-AB^{2}}$,将$BC = 2x$,$AB = x$代入可得$AC=\sqrt{(2x)^{2}-x^{2}}=\sqrt{4x^{2}-x^{2}}=\sqrt{3x^{2}}=\sqrt{3}x$。
因为四边形$AECF$是菱形,所以$AE = CE$。
又因为$BC = 2AB$,$AB\perp AC$,$\angle ACB = 30^{\circ}$(在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于$30^{\circ}$,这里$AB=\frac{1}{2}BC$),所以$\angle B = 60^{\circ}$。
因为$AE = BE$($AE = CE$,$BC = 2AB$,$AB = BE$),所以$\triangle ABE$是等边三角形,则$AE = AB$,$\angle AEB = 60^{\circ}$,所以$\angle AEC = 120^{\circ}$。
因为四边形$ABCD$是平行四边形,$AD = BC$,$AD// BC$,$AB = CD$,又$AE = AB$,所以$AE = CD$。
因为$CE = AE$,$BC = 2AB$,所以$BE = AB = AE$,$CE = AB$,$AD = 2AB$,$AF = CE$,所以$FD = AB$,即$AE = FD$。
又因为$AD// BC$,所以$\angle DCE=\angle ADC$。
在$\triangle ADE$和$\triangle DCE$中,$\left\{\begin{array}{l}AE = CD\\\angle AED=\angle DCE\\ED = DE\end{array}\right.$($SAS$:边角边,$\angle AED = 180^{\circ}-\angle AEB=120^{\circ}$,$\angle DCE = 180^{\circ}-\angle BCD$,$\angle BCD = 60^{\circ}$,$\angle DCE = 120^{\circ}$)。
所以$\triangle ADE\cong\triangle DCE$,则$\angle ADE=\angle CDE$。
因为$AD// BC$,$\angle AEB = 60^{\circ}$,所以$\angle EAD=\angle AEB = 60^{\circ}$。
又因为$AD = 2AB$,$AE = AB$,所以$AD = 2AE$。
在$\triangle ADE$中,设$AE = a$,$AD = 2a$,过$E$作$EH\perp AD$于$H$。
因为$\angle EAH = 60^{\circ}$,$\angle AHE = 90^{\circ}$,所以$\angle AEH = 30^{\circ}$,则$AH=\frac{1}{2}AE=\frac{1}{2}a$,$EH=\sqrt{AE^{2}-AH^{2}}=\sqrt{a^{2}-\left(\frac{1}{2}a\right)^{2}}=\frac{\sqrt{3}}{2}a$,$HD=AD - AH=2a-\frac{1}{2}a=\frac{3}{2}a$。
根据勾股定理$DE=\sqrt{EH^{2}+HD^{2}}=\sqrt{\left(\frac{\sqrt{3}}{2}a\right)^{2}+\left(\frac{3}{2}a\right)^{2}}=\sqrt{\frac{3}{4}a^{2}+\frac{9}{4}a^{2}}=\sqrt{3}a$。
再根据勾股定理逆定理,$AE^{2}+DE^{2}=a^{2}+3a^{2}=4a^{2}$,$AD^{2}=(2a)^{2}=4a^{2}$。
所以$AE^{2}+DE^{2}=AD^{2}$,根据勾股定理逆定理可得$\angle AED = 90^{\circ}$,即$AE\perp DE$。
另一种方法:
(2)证明:
因为四边形$AECF$是菱形,所以$AE = CE$,$\angle EAC=\angle ECA$。
因为四边形$ABCD$是平行四边形,$AD = BC$,$AD// BC$,$AB = CD$。
设$AB = x$,则$BC = 2x$,在$Rt\triangle ABC$中,$\angle B = 60^{\circ}$,$\angle ACB = 30^{\circ}$。
因为$AE = BE$($AE = CE$,$BC = 2AB$),所以$\triangle ABE$是等边三角形,$AE = AB$,$\angle BAE = 60^{\circ}$。
因为$AD// BC$,所以$\angle EAD=\angle AEB = 60^{\circ}$,$AD = 2AB$,$AE = AB$,所以$AD = 2AE$。
连接$AC$,$BD$交于点$O$(平行四边形对角线互相平分),因为$AB\perp AC$,$O$是$BD$中点,$E$是$BC$中点($AE = CE$),所以$OE// CD$,$OE=\frac{1}{2}CD$(三角形中位线定理)。
又因为$AE = AB = CD$,$AD = 2AB$,$\overrightarrow{DE}=\overrightarrow{DC}+\overrightarrow{CE}$,$\overrightarrow{AE}=\overrightarrow{AB}$。
因为$\angle DAB = 120^{\circ}$($\angle B = 60^{\circ}$,$AD// BC$),$\vert\overrightarrow{AD}\vert = 2\vert\overrightarrow{AE}\vert$,$\vert\overrightarrow{AE}\vert=\vert\overrightarrow{CD}\vert$。
根据向量数量积公式$\overrightarrow{AE}\cdot\overrightarrow{DE}=\overrightarrow{AE}\cdot(\overrightarrow{DC}+\overrightarrow{CE})$,因为$\overrightarrow{AE}=\overrightarrow{DC}$,$\overrightarrow{CE}=-\overrightarrow{AE}$($AE = CE$,方向相反)。
$\overrightarrow{AE}\cdot\overrightarrow{DE}=\overrightarrow{AE}\cdot\overrightarrow{DC}+\overrightarrow{AE}\cdot\overrightarrow{CE}=\vert\overrightarrow{AE}\vert^{2}-\vert\overrightarrow{AE}\vert^{2}=0$。
因为$\overrightarrow{AE}\cdot\overrightarrow{DE} = 0$,所以$\overrightarrow{AE}\perp\overrightarrow{DE}$,即$AE\perp DE$。
综上,(1)四边形$AECF$是菱形;(2)$AE\perp DE$得证。
查看更多完整答案,请扫码查看


