《2025年全效学习学业评价方案九年级数学上册北师大版》

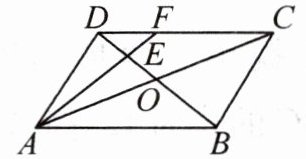
1. 如图，在$□ ABCD$中，$AC$与$BD$相交于点$O$，点$E$为$OD$的中点，连接$AE$并延长，交$DC$于点$F$，则$DF:FC=( )$D

A. $1:4$
B. $1:3$
C. $2:3$
D. $1:2$

答案： D

2. 如图，在$//ogram ABCD$中，点$E$在边$BC$上，点$F$在边$AD$的延长线上，且$DF=BE$，$EF$与$CD$交于点$G$.
(1)求证：$BD// EF$；
(2)若$\frac{DG}{GC}=\frac{2}{3}$，$BE=4$，求$EC$的长.

答案： 1. （1）证明：
因为四边形$ABCD$是平行四边形，所以$AD// BC$。
又因为$DF = BE$，所以四边形$BEFD$是平行四边形（一组对边平行且相等的四边形是平行四边形）。
所以$BD// EF$（平行四边形的对边平行）。
2. （2）解：
因为$AD// BC$，所以$\triangle DFG\sim\triangle CEG$。
根据相似三角形的性质，$\frac{DG}{GC}=\frac{DF}{EC}$。
已知$\frac{DG}{GC}=\frac{2}{3}$，$DF = BE = 4$。
设$EC=x$，则$\frac{2}{3}=\frac{4}{x}$。
交叉相乘得：$2x = 12$，解得$x = 6$。
所以$EC$的长为$6$。

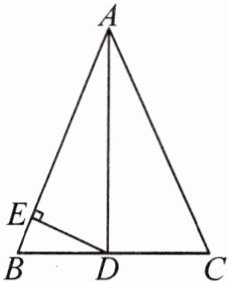
3. 如图，在$\triangle ABC$中，$AB=AC$，$AD$为$BC$边上的中线，$DE\perp AB$于点$E$.
(1)求证：$\triangle BDE\backsim\triangle CAD$；
(2)若$AB=13$，$BC=10$，求线段$DE$的长.

答案： 1. （1）证明：
因为$AB = AC$，$AD$为$BC$边上的中线，根据等腰三角形三线合一的性质，所以$AD\perp BC$，$\angle B=\angle C$。
又因为$DE\perp AB$，所以$\angle BED=\angle CDA = 90^{\circ}$。
在$\triangle BDE$和$\triangle CAD$中，$\left\{\begin{array}{l}\angle B=\angle C\\\angle BED=\angle CDA\end{array}\right.$。
根据两角分别相等的两个三角形相似，所以$\triangle BDE\backsim\triangle CAD$。
2. （2）解：
因为$AB = AC = 13$，$BC = 10$，$AD$是$BC$边上的中线，所以$BD=\frac{1}{2}BC = 5$。
在$Rt\triangle ABD$中，根据勾股定理$a^{2}+b^{2}=c^{2}$（这里$c = AB$，$a = BD$，$b = AD$），则$AD=\sqrt{AB^{2}-BD^{2}}$。
把$AB = 13$，$BD = 5$代入可得：$AD=\sqrt{13^{2}-5^{2}}=\sqrt{169 - 25}=\sqrt{144}=12$。
因为$\triangle BDE\backsim\triangle CAD$，所以$\frac{DE}{AD}=\frac{BD}{AC}$。
已知$AD = 12$，$BD = 5$，$AC = 13$，则$DE=\frac{BD\cdot AD}{AC}$。
把$BD = 5$，$AD = 12$，$AC = 13$代入可得：$DE=\frac{5×12}{13}=\frac{60}{13}$。
综上，（1）已证$\triangle BDE\backsim\triangle CAD$；（2）$DE$的长为$\frac{60}{13}$。

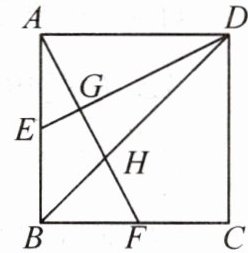
4. 如图，在正方形$ABCD$中，$E$，$F$分别是边$AB$和$BC$的中点，连接$AF$，$DE$，$BD$，$AF$分别交$DE$，$BD$于点$G$，$H$，求$AG:GH:HF$的值.

答案： $6:4:5$