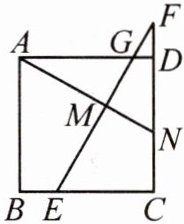
11. 如图,在正方形 $ABCD$ 中,$E$ 是边 $BC$ 上的一点,点 $F$ 在边 $CD$ 的延长线上,且 $BE = DF$,连接 $EF$ 交边 $AD$ 于点 $G$,过点 $A$ 作 $AN\perp EF$,垂足为 $M$,交边 $CD$ 于点 $N$。若 $BE = 5$,$CN = 8$,求线段 $AN$ 的长。

答案:
$4\sqrt{34}$
12. 如图 1,在矩形 $ABCD$ 中,$AB = CD = 8cm$,$AD = BC = 10cm$,点 $P$ 从点 $A$ 出发,沿 $A\to B\to C\to D$ 的路线运动,到点 $D$ 停止;点 $Q$ 从点 $D$ 出发,沿 $D\to C\to B\to A$ 的路线运动,到点 $A$ 停止。若点 $P$,$Q$ 同时出发,点 $P$ 的速度为 $1cm/s$,点 $Q$ 的速度为 $3cm/s$,运动 $a s$ 后,点 $P$,$Q$ 同时改变速度,点 $P$ 的速度变为 $b cm/s$,点 $Q$ 的速度变为 $d cm/s$,直到停止。图 2 是点 $P$ 出发 $x s$ 后,$\triangle APD$ 的面积 $S_1$(单位:$cm^2$)与运动时间 $x$(单位:$s$)的关系图象;图 3 是点 $Q$ 出发 $x s$ 后,$\triangle AQD$ 的面积 $S_2$(单位:$cm^2$)与运动时间 $x$(单位:$s$)的关系图象。
(1)根据图象得:$a =$
(2)设点 $P$ 已行的路程为 $y_1$(单位:$cm$),点 $Q$ 还剩的路程为 $y_2$(单位:$cm$),当 $x > a$ 时,请分别求出 $y_1$,$y_2$ 和运动时间 $x$ 的关系式;
(3)当 $x =$
(1)根据图象得:$a =$
6
,$b =$4
,$c =$11
,$d =$1
;(2)设点 $P$ 已行的路程为 $y_1$(单位:$cm$),点 $Q$ 还剩的路程为 $y_2$(单位:$cm$),当 $x > a$ 时,请分别求出 $y_1$,$y_2$ 和运动时间 $x$ 的关系式;
$y_{1}=4x-18(6<x\leqslant11)$;$y_{2}=14-x(6<x\leqslant14)$
(3)当 $x =$
$\frac{8}{5}$,5或$\frac{66}{7}$
时,$\triangle PBQ$ 为等腰三角形。
答案:
(1)6 4 11 1
(2)$y_{1}=4x-18(6<x\leqslant11)$;$y_{2}=14-x(6<x\leqslant14)$.
(3)$\frac{8}{5}$,5或$\frac{66}{7}$
(1)6 4 11 1
(2)$y_{1}=4x-18(6<x\leqslant11)$;$y_{2}=14-x(6<x\leqslant14)$.
(3)$\frac{8}{5}$,5或$\frac{66}{7}$
查看更多完整答案,请扫码查看


