1. 如图,正方形 $ABCD$ 的边长为 $4$,$\angle DAC$ 的平分线交 $DC$ 于点 $E$。若点 $P$,$Q$ 分别是 $AD$ 和 $AE$ 上的动点,则 $DQ + PQ$ 的最小值是
$ 2 \sqrt { 2 } $
。
答案:
$ 2 \sqrt { 2 } $
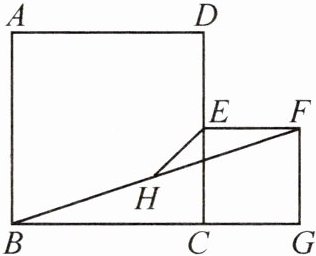
2. 如图,点 $G$ 是正方形 $ABCD$ 的 $BC$ 边延长线上一点,以 $CG$ 为边作正方形 $CGFE$,连接 $BF$,取线段 $BF$ 的中点 $H$,连接 $EH$。若 $AB = 4$,则线段 $EH$ 的最小值为______
$\sqrt{2}$
。
答案:
$ \sqrt { 2 } $
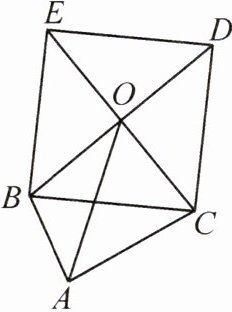
3. 如图,在 $\triangle ABC$ 中,$AB = 3$,$AC = 4$,以 $BC$ 为边在三角形外作正方形 $BCDE$,连接 $BD$,$CE$ 交于点 $O$,则线段 $AO$ 的最大值为______
$ \frac { 7 \sqrt { 2 } } { 2 } $
。
答案:
$ \frac { 7 \sqrt { 2 } } { 2 } $
4. 如图,在正方形 $ABCD$ 中,$AB = 4$,$AC$ 与 $BD$ 相交于点 $O$,$M$ 是 $AO$ 的中点,$P$,$Q$ 为对角线 $BD$ 上的两点。若 $PQ = \sqrt{2}$,则 $PM + CQ$ 的最小值为
$ 2 \sqrt { 5 } $
。
答案:
$ 2 \sqrt { 5 } $
5. 如图,已知正方形 $ABCD$ 的边长为 $6$,$F$ 是正方形内一点,连接 $CF$,$DF$,且 $\angle ADF = \angle DCF$,$E$ 是 $AD$ 边上一动点,连接 $EB$,$EF$,则 $EB + EF$ 的最小值为
$ 3 \sqrt { 13 } - 3 $
。
答案:
$ 3 \sqrt { 13 } - 3 $
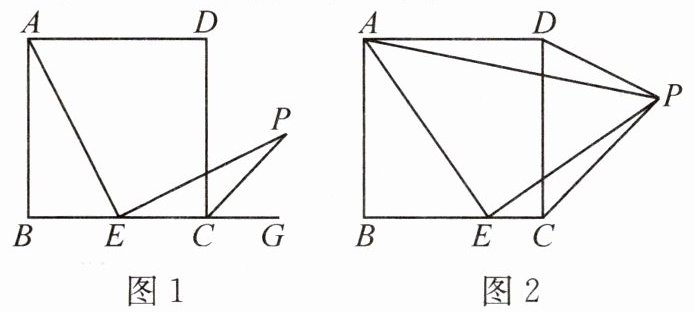
6. (1)如图 1,在正方形 $ABCD$ 中,$E$ 是 $BC$ 的中点,$AE \perp EP$,$EP$ 与正方形的外角 $\angle DCG$ 的平分线交于点 $P$。试猜想 $AE$ 与 $EP$ 的数量关系,并加以证明。
(2)如图 2,在正方形 $ABCD$ 中,$E$ 为 $BC$ 边上一动点(点 $E$,$B$ 不重合),$\triangle AEP$ 是等腰直角三角形,$\angle AEP = 90^{\circ}$,连接 $CP$,求 $\angle DCP$ 的度数。
(3)在(2)的条件下,连接 $DP$。若 $AB = 4$,求 $\triangle ADP$ 周长的最小值。
(2)如图 2,在正方形 $ABCD$ 中,$E$ 为 $BC$ 边上一动点(点 $E$,$B$ 不重合),$\triangle AEP$ 是等腰直角三角形,$\angle AEP = 90^{\circ}$,连接 $CP$,求 $\angle DCP$ 的度数。
(3)在(2)的条件下,连接 $DP$。若 $AB = 4$,求 $\triangle ADP$ 周长的最小值。

答案:
1. (1)
猜想:$AE = EP$。
证明:
取$AB$中点$F$,连接$EF$。
因为四边形$ABCD$是正方形,所以$AB = BC$,$\angle B=\angle BCD = 90^{\circ}$。
因为$E$是$BC$中点,$F$是$AB$中点,所以$BF = BE$,$AF = EC$。
则$\angle BFE = 45^{\circ}$,所以$\angle AFE = 135^{\circ}$。
因为$CP$平分$\angle DCG$,所以$\angle PCG = 45^{\circ}$,$\angle ECP = 135^{\circ}$。
又因为$\angle BAE+\angle AEB = 90^{\circ}$,$\angle AEB+\angle PEC = 90^{\circ}$,所以$\angle BAE=\angle PEC$。
在$\triangle AFE$和$\triangle ECP$中:
$\left\{\begin{array}{l}\angle AFE=\angle ECP\\AF = EC\\\angle FAE=\angle CEP\end{array}\right.$
根据$ASA$(角 - 边 - 角)定理,$\triangle AFE\cong\triangle ECP$。
所以$AE = EP$。
2. (2)
过$P$作$PH\perp BC$交$BC$延长线于$H$,作$PM\perp CD$于$M$。
因为$\angle AEP = 90^{\circ}$,$\angle B = 90^{\circ}$,$\angle BAE+\angle AEB = 90^{\circ}$,$\angle AEB+\angle PEH = 90^{\circ}$,所以$\angle BAE=\angle PEH$。
又因为$AE = EP$,$\angle B=\angle H = 90^{\circ}$,所以$\triangle ABE\cong\triangle EHP(AAS)$。
则$BE = PH$,$AB = EH$。
因为$AB = BC$,所以$BC = EH$,即$BE = CH$。
所以$PH = CH$,又$PH\perp CH$,$PM\perp CD$,$\angle HCM = 90^{\circ}$,所以四边形$PMCH$是正方形。
所以$\angle DCP = 45^{\circ}$。
3. (3)
因为$\angle DCP = 45^{\circ}$,所以点$P$在与$CD$成$45^{\circ}$角的射线上。
作$A$关于直线$CP$的对称点$A'$。
连接$A'D$交$CP$于$P'$,当$P$与$P'$重合时,$\triangle ADP$周长最小。
因为$AB = 4$,$AD = 4$。
由对称性质可知$A'C = AC=\sqrt{4^{2}+4^{2}} = 4\sqrt{2}$,$\angle A'CD=\angle ACD + \angle ACA'=45^{\circ}+45^{\circ}=90^{\circ}$。
所以$A'D=\sqrt{(4\sqrt{2})^{2}+4^{2}}=\sqrt{32 + 16}=\sqrt{48}=4\sqrt{3}$。
$\triangle ADP$周长$=AD + DP+AP=AD + DP + A'P$,其最小值为$AD + A'D$。
所以$\triangle ADP$周长最小值为$4 + 4\sqrt{3}$。
综上,(1)$AE = EP$;(2)$45^{\circ}$;(3)$4 + 4\sqrt{3}$。
猜想:$AE = EP$。
证明:
取$AB$中点$F$,连接$EF$。
因为四边形$ABCD$是正方形,所以$AB = BC$,$\angle B=\angle BCD = 90^{\circ}$。
因为$E$是$BC$中点,$F$是$AB$中点,所以$BF = BE$,$AF = EC$。
则$\angle BFE = 45^{\circ}$,所以$\angle AFE = 135^{\circ}$。
因为$CP$平分$\angle DCG$,所以$\angle PCG = 45^{\circ}$,$\angle ECP = 135^{\circ}$。
又因为$\angle BAE+\angle AEB = 90^{\circ}$,$\angle AEB+\angle PEC = 90^{\circ}$,所以$\angle BAE=\angle PEC$。
在$\triangle AFE$和$\triangle ECP$中:
$\left\{\begin{array}{l}\angle AFE=\angle ECP\\AF = EC\\\angle FAE=\angle CEP\end{array}\right.$
根据$ASA$(角 - 边 - 角)定理,$\triangle AFE\cong\triangle ECP$。
所以$AE = EP$。
2. (2)
过$P$作$PH\perp BC$交$BC$延长线于$H$,作$PM\perp CD$于$M$。
因为$\angle AEP = 90^{\circ}$,$\angle B = 90^{\circ}$,$\angle BAE+\angle AEB = 90^{\circ}$,$\angle AEB+\angle PEH = 90^{\circ}$,所以$\angle BAE=\angle PEH$。
又因为$AE = EP$,$\angle B=\angle H = 90^{\circ}$,所以$\triangle ABE\cong\triangle EHP(AAS)$。
则$BE = PH$,$AB = EH$。
因为$AB = BC$,所以$BC = EH$,即$BE = CH$。
所以$PH = CH$,又$PH\perp CH$,$PM\perp CD$,$\angle HCM = 90^{\circ}$,所以四边形$PMCH$是正方形。
所以$\angle DCP = 45^{\circ}$。
3. (3)
因为$\angle DCP = 45^{\circ}$,所以点$P$在与$CD$成$45^{\circ}$角的射线上。
作$A$关于直线$CP$的对称点$A'$。
连接$A'D$交$CP$于$P'$,当$P$与$P'$重合时,$\triangle ADP$周长最小。
因为$AB = 4$,$AD = 4$。
由对称性质可知$A'C = AC=\sqrt{4^{2}+4^{2}} = 4\sqrt{2}$,$\angle A'CD=\angle ACD + \angle ACA'=45^{\circ}+45^{\circ}=90^{\circ}$。
所以$A'D=\sqrt{(4\sqrt{2})^{2}+4^{2}}=\sqrt{32 + 16}=\sqrt{48}=4\sqrt{3}$。
$\triangle ADP$周长$=AD + DP+AP=AD + DP + A'P$,其最小值为$AD + A'D$。
所以$\triangle ADP$周长最小值为$4 + 4\sqrt{3}$。
综上,(1)$AE = EP$;(2)$45^{\circ}$;(3)$4 + 4\sqrt{3}$。
查看更多完整答案,请扫码查看


