7. 如图,四边形ABCD是正方形,E是平面内异于点A的任意一点,以线段AE为边作正方形AEFG,连接EB,GD.
(1)如图1,请判断EB与GD的位置关系,并证明你的结论;
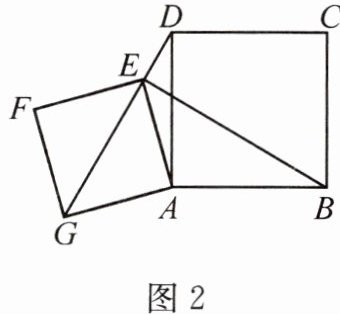
(2)如图2,若点E在线段DG上,$∠DAE=15^{\circ },AG=4$,求BE的长.
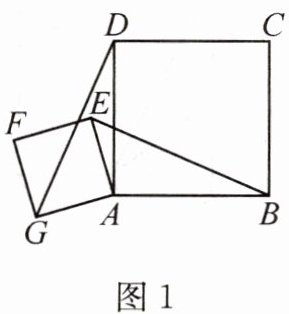
(1)如图1,请判断EB与GD的位置关系,并证明你的结论;
(2)如图2,若点E在线段DG上,$∠DAE=15^{\circ },AG=4$,求BE的长.


答案:
$(1)$ 判断$EB$与$GD$的位置关系并证明
解(证明):
因为四边形$ABCD$和四边形$AEFG$都是正方形,
所以$AB = AD$,$AE = AG$,$\angle BAD=\angle EAG = 90^{\circ}$。
$\angle BAD-\angle EAD=\angle EAG-\angle EAD$,即$\angle BAE=\angle DAG$。
在$\triangle BAE$和$\triangle DAG$中,
$\begin{cases}AB = AD\\\angle BAE=\angle DAG\\AE = AG\end{cases}$
根据$SAS$(边角边)定理可得$\triangle BAE\cong\triangle DAG$。
所以$\angle ABE=\angle ADG$。
设$AB$与$DG$相交于点$H$,
在$\triangle AHD$中,$\angle AHD + \angle ADG=90^{\circ}$,
因为$\angle ABE=\angle ADG$,$\angle AHD=\angle BHE$(对顶角相等),
所以在$\triangle BHE$中,$\angle BHE+\angle ABE = 90^{\circ}$,
则$\angle BEH=180^{\circ}-(\angle BHE+\angle ABE)=90^{\circ}$,
所以$EB\perp GD$。
$(2)$ 求$BE$的长
解:
因为四边形$AEFG$是正方形,$AG = 4$,所以$AE=AG = 4$,$\angle AEG = 45^{\circ}$。
因为$\angle DAE=15^{\circ}$,所以$\angle ADG=\angle ABE$(由$(1)$中$\triangle BAE\cong\triangle DAG$得到),
$\angle AED=\angle DAE+\angle ADG$(三角形外角性质),
又因为$\angle AED = 180^{\circ}-\angle AEG=180 - 45^{\circ}=135^{\circ}$,
所以$\angle ADG=\angle AED-\angle DAE=135^{\circ}-15^{\circ}=120^{\circ}$,则$\angle ABE = 30^{\circ}$。
过点$A$作$AM\perp BE$于点$M$,
在$Rt\triangle AEM$中,$\angle AEM = 45^{\circ}$,$AE = 4$,
根据$\sin\angle AEM=\frac{AM}{AE}$,$\cos\angle AEM=\frac{EM}{AE}$,可得$AM = EM=AE\sin45^{\circ}=4×\frac{\sqrt{2}}{2}=2\sqrt{2}$。
在$Rt\triangle ABM$中,$\angle ABE = 30^{\circ}$,$AM = 2\sqrt{2}$,
根据$\tan\angle ABE=\frac{AM}{BM}$,可得$BM=\frac{AM}{\tan30^{\circ}}=\frac{2\sqrt{2}}{\frac{\sqrt{3}}{3}} = 2\sqrt{6}$。
所以$BE=BM + EM=2\sqrt{6}+2\sqrt{2}$。
综上,$(1)$$\boldsymbol{EB\perp GD}$;$(2)$$\boldsymbol{BE = 2\sqrt{6}+2\sqrt{2}}$。
解(证明):
因为四边形$ABCD$和四边形$AEFG$都是正方形,
所以$AB = AD$,$AE = AG$,$\angle BAD=\angle EAG = 90^{\circ}$。
$\angle BAD-\angle EAD=\angle EAG-\angle EAD$,即$\angle BAE=\angle DAG$。
在$\triangle BAE$和$\triangle DAG$中,
$\begin{cases}AB = AD\\\angle BAE=\angle DAG\\AE = AG\end{cases}$
根据$SAS$(边角边)定理可得$\triangle BAE\cong\triangle DAG$。
所以$\angle ABE=\angle ADG$。
设$AB$与$DG$相交于点$H$,
在$\triangle AHD$中,$\angle AHD + \angle ADG=90^{\circ}$,
因为$\angle ABE=\angle ADG$,$\angle AHD=\angle BHE$(对顶角相等),
所以在$\triangle BHE$中,$\angle BHE+\angle ABE = 90^{\circ}$,
则$\angle BEH=180^{\circ}-(\angle BHE+\angle ABE)=90^{\circ}$,
所以$EB\perp GD$。
$(2)$ 求$BE$的长
解:
因为四边形$AEFG$是正方形,$AG = 4$,所以$AE=AG = 4$,$\angle AEG = 45^{\circ}$。
因为$\angle DAE=15^{\circ}$,所以$\angle ADG=\angle ABE$(由$(1)$中$\triangle BAE\cong\triangle DAG$得到),
$\angle AED=\angle DAE+\angle ADG$(三角形外角性质),
又因为$\angle AED = 180^{\circ}-\angle AEG=180 - 45^{\circ}=135^{\circ}$,
所以$\angle ADG=\angle AED-\angle DAE=135^{\circ}-15^{\circ}=120^{\circ}$,则$\angle ABE = 30^{\circ}$。
过点$A$作$AM\perp BE$于点$M$,
在$Rt\triangle AEM$中,$\angle AEM = 45^{\circ}$,$AE = 4$,
根据$\sin\angle AEM=\frac{AM}{AE}$,$\cos\angle AEM=\frac{EM}{AE}$,可得$AM = EM=AE\sin45^{\circ}=4×\frac{\sqrt{2}}{2}=2\sqrt{2}$。
在$Rt\triangle ABM$中,$\angle ABE = 30^{\circ}$,$AM = 2\sqrt{2}$,
根据$\tan\angle ABE=\frac{AM}{BM}$,可得$BM=\frac{AM}{\tan30^{\circ}}=\frac{2\sqrt{2}}{\frac{\sqrt{3}}{3}} = 2\sqrt{6}$。
所以$BE=BM + EM=2\sqrt{6}+2\sqrt{2}$。
综上,$(1)$$\boldsymbol{EB\perp GD}$;$(2)$$\boldsymbol{BE = 2\sqrt{6}+2\sqrt{2}}$。
8. 在正方形ABCD中,M为射线CD上一点(不与D重合),以CM为边,在正方形ABCD的异侧作正方形CFGM,连接BM,DF,直线BM与直线DF交于点E.
(1)如图1,若点M在CD的延长线上,求证:$DF=BM,DF⊥BM.$
(2)如图2,若点M移到边CD上.
①在(1)中的结论是否仍成立?(直接回答不需证明)
②连接BD,若$BD=BF$,且正方形CFGM的边长为1,求正方形ABCD的周长.
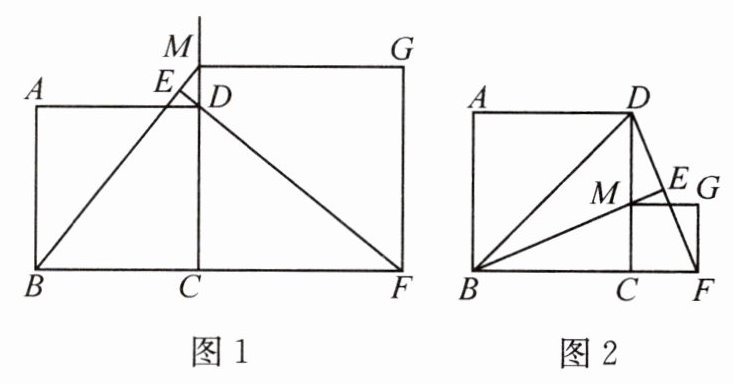
(1)如图1,若点M在CD的延长线上,求证:$DF=BM,DF⊥BM.$
(2)如图2,若点M移到边CD上.
①在(1)中的结论是否仍成立?(直接回答不需证明)
②连接BD,若$BD=BF$,且正方形CFGM的边长为1,求正方形ABCD的周长.

答案:
1. (1)证明:
因为四边形$ABCD$和四边形$CFGM$是正方形,
所以$BC = CD$,$CM = CF$,$\angle BCD=\angle DCF = 90^{\circ}$。
在$\triangle BCM$和$\triangle DCF$中,
根据$SAS$(边角边)判定定理,$\left\{\begin{array}{l}BC = CD\\\angle BCM=\angle DCF\\CM = CF\end{array}\right.$。
所以$\triangle BCM\cong\triangle DCF$。
则$BM = DF$,$\angle CBM=\angle CDF$。
又因为$\angle BMC+\angle CBM = 90^{\circ}$,$\angle BMC=\angle DME$(对顶角相等)。
所以$\angle DME+\angle CDF = 90^{\circ}$。
在$\triangle DME$中,$\angle DEM=180^{\circ}-(\angle DME + \angle CDF)=90^{\circ}$,即$DF\perp BM$。
2. (2)①
结论仍然成立,即$DF = BM$,$DF\perp BM$。
3. (2)②
设正方形$ABCD$的边长为$x$。
因为正方形$CFGM$的边长为$1$,所以$CF = CM = 1$,则$BM=\sqrt{BC^{2}+CM^{2}}=\sqrt{x^{2}+1}$。
因为四边形$ABCD$是正方形,所以$BD=\sqrt{2}x$。
又因为$BD = BF$,$BF=BC + CF=x + 1$。
所以$\sqrt{2}x=x + 1$。
移项可得$\sqrt{2}x-x = 1$,即$x(\sqrt{2}-1)=1$。
解得$x=\frac{1}{\sqrt{2}-1}=\sqrt{2}+1$。
那么正方形$ABCD$的周长$C = 4x=4(\sqrt{2}+1)=4\sqrt{2}+4$。
综上,(1)得证;(2)①结论成立;(2)②正方形$ABCD$的周长为$4\sqrt{2}+4$。
因为四边形$ABCD$和四边形$CFGM$是正方形,
所以$BC = CD$,$CM = CF$,$\angle BCD=\angle DCF = 90^{\circ}$。
在$\triangle BCM$和$\triangle DCF$中,
根据$SAS$(边角边)判定定理,$\left\{\begin{array}{l}BC = CD\\\angle BCM=\angle DCF\\CM = CF\end{array}\right.$。
所以$\triangle BCM\cong\triangle DCF$。
则$BM = DF$,$\angle CBM=\angle CDF$。
又因为$\angle BMC+\angle CBM = 90^{\circ}$,$\angle BMC=\angle DME$(对顶角相等)。
所以$\angle DME+\angle CDF = 90^{\circ}$。
在$\triangle DME$中,$\angle DEM=180^{\circ}-(\angle DME + \angle CDF)=90^{\circ}$,即$DF\perp BM$。
2. (2)①
结论仍然成立,即$DF = BM$,$DF\perp BM$。
3. (2)②
设正方形$ABCD$的边长为$x$。
因为正方形$CFGM$的边长为$1$,所以$CF = CM = 1$,则$BM=\sqrt{BC^{2}+CM^{2}}=\sqrt{x^{2}+1}$。
因为四边形$ABCD$是正方形,所以$BD=\sqrt{2}x$。
又因为$BD = BF$,$BF=BC + CF=x + 1$。
所以$\sqrt{2}x=x + 1$。
移项可得$\sqrt{2}x-x = 1$,即$x(\sqrt{2}-1)=1$。
解得$x=\frac{1}{\sqrt{2}-1}=\sqrt{2}+1$。
那么正方形$ABCD$的周长$C = 4x=4(\sqrt{2}+1)=4\sqrt{2}+4$。
综上,(1)得证;(2)①结论成立;(2)②正方形$ABCD$的周长为$4\sqrt{2}+4$。
查看更多完整答案,请扫码查看


