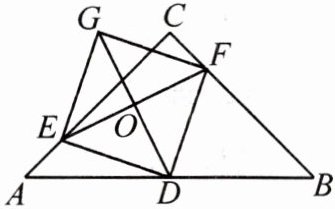
例 3 如图,在等腰直角三角形 $ABC$ 中,$\angle ACB = 90^{\circ}$,$AC = BC = 4$,$D$ 是 $AB$ 的中点,$E$,$F$ 分别是 $AC$,$BC$ 上的点(点 $E$ 不与点 $A$,$C$ 重合),且 $AE = CF$,连接 $EF$ 并取 $EF$ 的中点 $O$,连接 $DO$ 并延长至点 $G$,使 $GO = DO$,连接 $DE$,$DF$,$GE$,$GF$。
(1)求证:四边形 $EDFG$ 是正方形;
(2)当点 $E$ 在什么位置时,四边形 $EDFG$ 的面积最小?并求四边形 $EDFG$ 面积的最小值。
(1)求证:四边形 $EDFG$ 是正方形;
(2)当点 $E$ 在什么位置时,四边形 $EDFG$ 的面积最小?并求四边形 $EDFG$ 面积的最小值。

答案:
1. (1)**证明四边形$EDFG$是正方形**:
连接$CD$。
因为$\triangle ABC$是等腰直角三角形,$\angle ACB = 90^{\circ}$,$AC = BC = 4$,$D$是$AB$中点,根据等腰直角三角形三线合一性质,$CD = AD = BD$,$\angle A=\angle DCF = 45^{\circ}$,$CD\perp AB$。
又因为$AE = CF$,在$\triangle ADE$和$\triangle CDF$中,$\begin{cases}AD = CD\\\angle A=\angle DCF\\AE = CF\end{cases}$,根据$SAS$(边角边)定理,$\triangle ADE\cong\triangle CDF$。
所以$DE = DF$,$\angle ADE=\angle CDF$。
因为$\angle ADE+\angle CDE = 90^{\circ}$,所以$\angle CDF+\angle CDE=\angle EDF = 90^{\circ}$。
因为$O$是$EF$中点,$GO = DO$,所以四边形$EDFG$是平行四边形(对角线互相平分的四边形是平行四边形)。
又因为$DE = DF$,$\angle EDF = 90^{\circ}$,所以平行四边形$EDFG$是正方形(一组邻边相等且有一个角是直角的平行四边形是正方形)。
2. (2)**求四边形$EDFG$面积最小时$E$的位置及面积最小值**:
设$AE=x$,则$CF = x$,$CE=4 - x$。
在$Rt\triangle CEF$中,根据勾股定理$EF^{2}=CE^{2}+CF^{2}=(4 - x)^{2}+x^{2}$。
展开$(4 - x)^{2}+x^{2}=16-8x + x^{2}+x^{2}=2x^{2}-8x + 16$。
配方得$2x^{2}-8x + 16=2(x - 2)^{2}+8$。
因为四边形$EDFG$是正方形,其面积$S = DE^{2}$(正方形面积等于边长的平方),又因为$DE = DF$,$\angle EDF = 90^{\circ}$,$S=\frac{1}{2}EF^{2}$(正方形面积还可以用对角线乘积的一半表示,这里$EF$为正方形$EDFG$的对角线,$DE = DF$,$EF=\sqrt{2}DE$,$S = DE^{2}=\frac{1}{2}EF^{2}$)。
由$EF^{2}=2(x - 2)^{2}+8$,因为$2\gt0$,所以当$x = 2$时,$EF^{2}$取得最小值$8$。
此时$S=\frac{1}{2}×8 = 4$,即当$E$为$AC$中点时,四边形$EDFG$的面积最小,最小值为$4$。
综上,(1)已证得四边形$EDFG$是正方形;(2)当$E$为$AC$中点时,四边形$EDFG$面积最小,最小值为$4$。
连接$CD$。
因为$\triangle ABC$是等腰直角三角形,$\angle ACB = 90^{\circ}$,$AC = BC = 4$,$D$是$AB$中点,根据等腰直角三角形三线合一性质,$CD = AD = BD$,$\angle A=\angle DCF = 45^{\circ}$,$CD\perp AB$。
又因为$AE = CF$,在$\triangle ADE$和$\triangle CDF$中,$\begin{cases}AD = CD\\\angle A=\angle DCF\\AE = CF\end{cases}$,根据$SAS$(边角边)定理,$\triangle ADE\cong\triangle CDF$。
所以$DE = DF$,$\angle ADE=\angle CDF$。
因为$\angle ADE+\angle CDE = 90^{\circ}$,所以$\angle CDF+\angle CDE=\angle EDF = 90^{\circ}$。
因为$O$是$EF$中点,$GO = DO$,所以四边形$EDFG$是平行四边形(对角线互相平分的四边形是平行四边形)。
又因为$DE = DF$,$\angle EDF = 90^{\circ}$,所以平行四边形$EDFG$是正方形(一组邻边相等且有一个角是直角的平行四边形是正方形)。
2. (2)**求四边形$EDFG$面积最小时$E$的位置及面积最小值**:
设$AE=x$,则$CF = x$,$CE=4 - x$。
在$Rt\triangle CEF$中,根据勾股定理$EF^{2}=CE^{2}+CF^{2}=(4 - x)^{2}+x^{2}$。
展开$(4 - x)^{2}+x^{2}=16-8x + x^{2}+x^{2}=2x^{2}-8x + 16$。
配方得$2x^{2}-8x + 16=2(x - 2)^{2}+8$。
因为四边形$EDFG$是正方形,其面积$S = DE^{2}$(正方形面积等于边长的平方),又因为$DE = DF$,$\angle EDF = 90^{\circ}$,$S=\frac{1}{2}EF^{2}$(正方形面积还可以用对角线乘积的一半表示,这里$EF$为正方形$EDFG$的对角线,$DE = DF$,$EF=\sqrt{2}DE$,$S = DE^{2}=\frac{1}{2}EF^{2}$)。
由$EF^{2}=2(x - 2)^{2}+8$,因为$2\gt0$,所以当$x = 2$时,$EF^{2}$取得最小值$8$。
此时$S=\frac{1}{2}×8 = 4$,即当$E$为$AC$中点时,四边形$EDFG$的面积最小,最小值为$4$。
综上,(1)已证得四边形$EDFG$是正方形;(2)当$E$为$AC$中点时,四边形$EDFG$面积最小,最小值为$4$。
(3)点 $P$ 在直线 $DE$ 上,且 $\triangle PEF$ 为等腰三角形,则点 $P$ 的坐标为
$(2\sqrt{5},4\sqrt{5}+2)$或$(-2\sqrt{5},-4\sqrt{5}+2)$或$(2.5,7)$或$(8,18)$
。
答案:
(1)点F的坐标为$(8,8)$.
(2)存在,理由略.当$S_{\triangle QDE}=S_{\triangle CDE}$时,点Q的坐标为$(-6,0),(4,0)$.
(3)$(2\sqrt{5},4\sqrt{5}+2)$或$(-2\sqrt{5},-4\sqrt{5}+2)$或$(2.5,7)$或$(8,18)$
(1)点F的坐标为$(8,8)$.
(2)存在,理由略.当$S_{\triangle QDE}=S_{\triangle CDE}$时,点Q的坐标为$(-6,0),(4,0)$.
(3)$(2\sqrt{5},4\sqrt{5}+2)$或$(-2\sqrt{5},-4\sqrt{5}+2)$或$(2.5,7)$或$(8,18)$
查看更多完整答案,请扫码查看


