5. 如图,在正方形ABCD中,E,F分别是AB,BC的中点,CE,DF相交于点G,连接AG.求证:
(1)$CE⊥DF;$
(2)$∠AGE=∠CDF.$

(1)$CE⊥DF;$
(2)$∠AGE=∠CDF.$

答案:
【解析】:
(1) 因为四边形$ABCD$是正方形,所以$AB = BC = CD$,$\angle B=\angle BCD = 90^{\circ}$。
又因为$E$,$F$分别是$AB$,$BC$的中点,所以$BE=\frac{1}{2}AB$,$CF = \frac{1}{2}BC$,则$BE = CF$。
在$\triangle CBE$和$\triangle DCF$中,$\begin{cases}BC = CD\\\angle B=\angle BCD\\BE = CF\end{cases}$,根据$SAS$(边角边)定理可得$\triangle CBE\cong\triangle DCF$。
所以$\angle BCE=\angle CDF$。
因为$\angle BCE+\angle DCE = 90^{\circ}$,所以$\angle CDF+\angle DCE = 90^{\circ}$,在$\triangle DGC$中,$\angle DGC=180^{\circ}-(\angle CDF+\angle DCE)=90^{\circ}$,即$CE\perp DF$。
(2) 延长$CE$,$DA$交于点$M$。
因为$E$是$AB$的中点,$AB// CD$,所以$\angle MAE=\angle B = 90^{\circ}$,$\angle M=\angle BCE$。
在$\triangle AEM$和$\triangle BEC$中,$\begin{cases}\angle MAE=\angle B\\\angle M=\angle BCE\\AE = BE\end{cases}$,根据$AAS$(角角边)定理可得$\triangle AEM\cong\triangle BEC$,所以$AM = BC$。
因为$BC = AD$,所以$AM = AD$。
又因为$CE\perp DF$,所以$AG = AM = AD$,则$\angle M=\angle AGE$。
由
(1)知$\angle M=\angle BCE=\angle CDF$,所以$\angle AGE=\angle CDF$。
【答案】:
(1) 证明见上述解析,证得$CE\perp DF$。
(2) 证明见上述解析,证得$\angle AGE=\angle CDF$。
(1) 因为四边形$ABCD$是正方形,所以$AB = BC = CD$,$\angle B=\angle BCD = 90^{\circ}$。
又因为$E$,$F$分别是$AB$,$BC$的中点,所以$BE=\frac{1}{2}AB$,$CF = \frac{1}{2}BC$,则$BE = CF$。
在$\triangle CBE$和$\triangle DCF$中,$\begin{cases}BC = CD\\\angle B=\angle BCD\\BE = CF\end{cases}$,根据$SAS$(边角边)定理可得$\triangle CBE\cong\triangle DCF$。
所以$\angle BCE=\angle CDF$。
因为$\angle BCE+\angle DCE = 90^{\circ}$,所以$\angle CDF+\angle DCE = 90^{\circ}$,在$\triangle DGC$中,$\angle DGC=180^{\circ}-(\angle CDF+\angle DCE)=90^{\circ}$,即$CE\perp DF$。
(2) 延长$CE$,$DA$交于点$M$。
因为$E$是$AB$的中点,$AB// CD$,所以$\angle MAE=\angle B = 90^{\circ}$,$\angle M=\angle BCE$。
在$\triangle AEM$和$\triangle BEC$中,$\begin{cases}\angle MAE=\angle B\\\angle M=\angle BCE\\AE = BE\end{cases}$,根据$AAS$(角角边)定理可得$\triangle AEM\cong\triangle BEC$,所以$AM = BC$。
因为$BC = AD$,所以$AM = AD$。
又因为$CE\perp DF$,所以$AG = AM = AD$,则$\angle M=\angle AGE$。
由
(1)知$\angle M=\angle BCE=\angle CDF$,所以$\angle AGE=\angle CDF$。
【答案】:
(1) 证明见上述解析,证得$CE\perp DF$。
(2) 证明见上述解析,证得$\angle AGE=\angle CDF$。
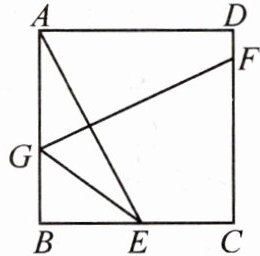
6. [2024·鹿城区开学]如图,在正方形ABCD中,E为BC边上的点,连接AE,作AE的垂直平分线交AB于点G,交CD于点F,连接GE.已知$\frac {BG}{BE}=\frac {3}{4}.$
(1)若正方形的边长为4,求BG的长;
(2)求证:$\frac {DF}{CF}=\frac {1}{7}.$
(1)若正方形的边长为4,求BG的长;
(2)求证:$\frac {DF}{CF}=\frac {1}{7}.$

答案:
1. (1)
设$BG = 3x$,因为$\frac{BG}{BE}=\frac{3}{4}$,所以$BE = 4x$。
因为$GF$是$AE$的垂直平分线,所以$AG = GE$。
已知正方形边长$AB = 4$,则$AG=AB - BG=4 - 3x$,$GE = 4 - 3x$。
在$Rt\triangle BGE$中,根据勾股定理$GE^{2}=BG^{2}+BE^{2}$,即$(4 - 3x)^{2}=(3x)^{2}+(4x)^{2}$。
展开式子:
$16-24x + 9x^{2}=9x^{2}+16x^{2}$。
移项可得$16x^{2}+24x - 16 = 0$,两边同时除以$8$得$2x^{2}+3x - 2 = 0$。
分解因式得$(2x - 1)(x + 2)=0$。
解得$x=\frac{1}{2}$或$x=-2$(边长不能为负舍去)。
所以$BG = 3x=\frac{3}{2}$。
2. (2)
证明:过点$F$作$FH\perp AB$于$H$。
因为四边形$ABCD$是正方形,所以$AB = BC = CD = DA$,$\angle B=\angle C=\angle D=\angle AHF = 90^{\circ}$,$FH = BC = AB$。
设$BG = 3a$,$BE = 4a$,则$GE=AG = AB - BG$,在$Rt\triangle BGE$中,$GE=\sqrt{BG^{2}+BE^{2}}=\sqrt{(3a)^{2}+(4a)^{2}} = 5a$,所以$AB=AG + BG=8a$。
因为$\angle AGE+\angle BGE = 90^{\circ}$,$\angle BGE+\angle BEG = 90^{\circ}$,所以$\angle AGE=\angle BEG$。
又因为$\angle B=\angle AHF = 90^{\circ}$,$FH = AB$,所以$\triangle ABE\cong\triangle FHG(AAS)$。
则$HG = BE = 4a$,$AH = AB - BH=AB - CF$,$DF = AH$。
因为$HG = BE = 4a$,$BG = 3a$,所以$AH=DF=a$,$CF=CD - DF=8a - a = 7a$。
所以$\frac{DF}{CF}=\frac{a}{7a}=\frac{1}{7}$。
综上,(1)$BG$的长为$\frac{3}{2}$;(2)证明如上。
设$BG = 3x$,因为$\frac{BG}{BE}=\frac{3}{4}$,所以$BE = 4x$。
因为$GF$是$AE$的垂直平分线,所以$AG = GE$。
已知正方形边长$AB = 4$,则$AG=AB - BG=4 - 3x$,$GE = 4 - 3x$。
在$Rt\triangle BGE$中,根据勾股定理$GE^{2}=BG^{2}+BE^{2}$,即$(4 - 3x)^{2}=(3x)^{2}+(4x)^{2}$。
展开式子:
$16-24x + 9x^{2}=9x^{2}+16x^{2}$。
移项可得$16x^{2}+24x - 16 = 0$,两边同时除以$8$得$2x^{2}+3x - 2 = 0$。
分解因式得$(2x - 1)(x + 2)=0$。
解得$x=\frac{1}{2}$或$x=-2$(边长不能为负舍去)。
所以$BG = 3x=\frac{3}{2}$。
2. (2)
证明:过点$F$作$FH\perp AB$于$H$。
因为四边形$ABCD$是正方形,所以$AB = BC = CD = DA$,$\angle B=\angle C=\angle D=\angle AHF = 90^{\circ}$,$FH = BC = AB$。
设$BG = 3a$,$BE = 4a$,则$GE=AG = AB - BG$,在$Rt\triangle BGE$中,$GE=\sqrt{BG^{2}+BE^{2}}=\sqrt{(3a)^{2}+(4a)^{2}} = 5a$,所以$AB=AG + BG=8a$。
因为$\angle AGE+\angle BGE = 90^{\circ}$,$\angle BGE+\angle BEG = 90^{\circ}$,所以$\angle AGE=\angle BEG$。
又因为$\angle B=\angle AHF = 90^{\circ}$,$FH = AB$,所以$\triangle ABE\cong\triangle FHG(AAS)$。
则$HG = BE = 4a$,$AH = AB - BH=AB - CF$,$DF = AH$。
因为$HG = BE = 4a$,$BG = 3a$,所以$AH=DF=a$,$CF=CD - DF=8a - a = 7a$。
所以$\frac{DF}{CF}=\frac{a}{7a}=\frac{1}{7}$。
综上,(1)$BG$的长为$\frac{3}{2}$;(2)证明如上。
查看更多完整答案,请扫码查看


