《2025年全效学习学业评价方案九年级数学上册北师大版》

9. 如图，在 $□ ABCD$ 中，对角线 $AC$，$BD$ 相交于点 $O$，$E$，$F$ 分别为 $OB$，$OD$ 的中点，延长 $AE$ 至点 $G$，使 $EG = AE$，连接 $CG$。
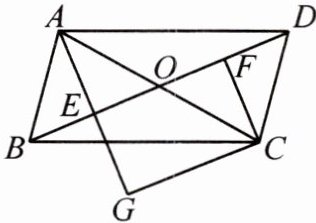
(1)求证：$\triangle ABE\cong\triangle CDF$。
(2)当 $AB$ 与 $AC$ 满足什么数量关系时，四边形 $EGCF$ 是矩形？请说明理由。

答案： 1. （1）证明：
因为四边形$ABCD$是平行四边形，所以$AB = CD$，$AB// CD$，$OB = OD$，$OA = OC$。
所以$\angle ABE=\angle CDF$。
又因为$E$，$F$分别为$OB$，$OD$的中点，所以$BE=\frac{1}{2}OB$，$DF = \frac{1}{2}OD$，则$BE = DF$。
在$\triangle ABE$和$\triangle CDF$中，$\begin{cases}AB = CD\\\angle ABE=\angle CDF\\BE = DF\end{cases}$。
根据$SAS$（边角边）定理，可得$\triangle ABE\cong\triangle CDF$。
2. （2）解：
当$AC = 2AB$时，四边形$EGCF$是矩形。
理由如下：
因为$AC = 2OA$，$AC = 2AB$，所以$AB = OA$。
因为$E$是$OB$的中点，所以$AG\perp OB$（等腰三角形三线合一），即$\angle AEG = 90^{\circ}$。
同理可证$CF\perp OD$。
因为$EG = AE$，$OA = OC$，所以$OE$是$\triangle ACG$的中位线。
根据三角形中位线定理：三角形的中位线平行于第三边，且等于第三边的一半，可得$OE// CG$，$OE=\frac{1}{2}CG$。
又因为$E$，$F$分别为$OB$，$OD$的中点，所以$EF=\frac{1}{2}BD$，且$OB = OD$，$OA = OC$，$AC\perp BD$（由$AB = OA$，$E$为$OB$中点推出$AG\perp OB$，同理$CF\perp OD$，进而$AC\perp BD$）。
因为$EG = AE$，$OA = OC$，所以$CG = 2OE$，又$EF=\frac{1}{2}BD$，$BD = 2OE$（平行四边形对角线互相平分，$E$为$OB$中点，$F$为$OD$中点，$EF=\frac{1}{2}(OB + OD)=\frac{1}{2}BD$，且$AC\perp BD$时，$OE=\frac{1}{2}AB$，$BD = 2AB$，这里$AC = 2AB$，$OA=AB$，$OB=\sqrt{OA^{2}-AE^{2}}$（$AE\perp OB$），通过平行四边形性质和中点关系），$EF = OE$，$CG// EF$。
又因为$\angle AEG = 90^{\circ}$，$CF\perp OD$，$AG// CF$（由$\triangle ABE\cong\triangle CDF$得$\angle BAE=\angle DCF$，$AB// CD$得$\angle BAC=\angle DCA$，所以$\angle EAC=\angle FCA$，所以$AG// CF$），$EG = AE$，$CF = AE$（$\triangle ABE\cong\triangle CDF$），所以$EG = CF$。
所以四边形$EGCF$是平行四边形（一组对边平行且相等的四边形是平行四边形），又因为$\angle AEG = 90^{\circ}$，所以四边形$EGCF$是矩形（有一个角是直角的平行四边形是矩形）。
综上，（1）已证$\triangle ABE\cong\triangle CDF$；（2）当$AC = 2AB$时，四边形$EGCF$是矩形。

10. 如图，在四边形 $ABCD$ 中，$AD// BC$，$\angle A = \angle D = 90^{\circ}$，$E$ 是 $AD$ 的中点，连接 $BE$，将 $\triangle ABE$ 沿 $BE$ 折叠后得到 $\triangle GBE$，且点 $G$ 在四边形 $ABCD$ 内部，延长 $BG$ 交 $DC$ 于点 $F$，连接 $EF$。
(1)求证：$\triangle EGF\cong\triangle EDF$；
(2)求证：$BG = CD$；
(3)若 $F$ 是 $CD$ 的中点，$BC = 8$，求 $CD$ 的长。

答案： 1. （1）证明：
因为$E$是$AD$的中点，所以$AE = DE$。
由折叠可知$AE = GE$，$\angle A=\angle BGE = 90^{\circ}$，所以$GE = DE$，$\angle EGF=\angle D = 90^{\circ}$。
在$Rt\triangle EGF$和$Rt\triangle EDF$中，$\left\{\begin{array}{l}EF = EF\\GE = DE\end{array}\right.$（$HL$定理：斜边和一条直角边对应相等的两个直角三角形全等）。
所以$\triangle EGF\cong\triangle EDF$。
2. （2）证明：
因为$AD// BC$，$\angle A=\angle D = 90^{\circ}$，所以$\angle C=\angle A=\angle D = 90^{\circ}$，四边形$ABCD$是矩形。
由（1）知$\triangle EGF\cong\triangle EDF$，所以$GF = DF$。
又因为$\triangle ABE\cong\triangle GBE$，所以$AB = GB$。
因为四边形$ABCD$是矩形，所以$AB = CD$，所以$BG = CD$。
3. （3）解：
设$DF = x$，因为$F$是$CD$的中点，所以$CD = 2x$，则$BG = 2x$，$GF = x$，$BF=BG + GF=3x$。
因为$BC = 8$，$\angle C = 90^{\circ}$，由勾股定理$BF^{2}=BC^{2}+CF^{2}$（$CF = DF=x$）。
即$(3x)^{2}=8^{2}+x^{2}$。
展开得$9x^{2}=64 + x^{2}$。
移项得$9x^{2}-x^{2}=64$，即$8x^{2}=64$。
两边同时除以$8$得$x^{2}=8$，解得$x = 2\sqrt{2}$（$x\gt0$）。
所以$CD = 2x = 4\sqrt{2}$。
综上，（1）证明见上述过程；（2）证明见上述过程；（3）$CD$的长为$4\sqrt{2}$。