《2025年一本通武汉出版社九年级数学上册北师大版核心板》

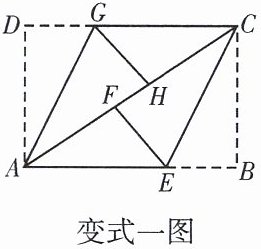
【变式一】如图,ABCD是矩形纸片,翻折∠B,∠D,使BC,AD恰好落在AC上. 设点F,H分别是B,D落在AC上的点,点E,G分别是折痕CE与AB,AG与CD的交点.
(1)求证：四边形AECG是平行四边形；
(2)若矩形的一边AB的长为3 cm,当BC的长为多少时,四边形AECG是菱形？

答案：
(1)证明：
∵四边形ABCD是矩形，
∴AB//CD，AD//BC，∠B=∠D=90°，
∴∠BAC=∠DCA，
由翻折性质得：∠GAH=∠DAG，∠ECF=∠BCE，
∵∠BAC=∠GAH+∠DAG，∠DCA=∠ECF+∠BCE，
∴∠GAH=∠ECF，
∴AG//CE，
又
∵AE//CG，
∴四边形AECG是平行四边形；
(2)解：设BC=x cm，AC=$\sqrt{AB^{2}+BC^{2}}=\sqrt{9+x^{2}}$ cm，
由翻折性质得：BF=EF，DF=GH，AF=AD=BC=x cm，CH=BC=x cm，
∵AC=AF+FH+CH，FH=AC - AF - CH=$\sqrt{9+x^{2}} - 2x$，
∵四边形AECG是菱形，
∴AE=CE，
设AE=CE=y cm，则BE=AB - AE=3 - y cm，
在Rt△BCE中，BE² + BC²=CE²，即(3 - y)² + x²=y²，
解得$y=\frac{x^{2}+9}{6}$，
∵AG//CE，AE//CG，
∴AG=CE=y，CG=AE=y，
在Rt△ADG中，DG=CD - CG=3 - y cm，AD=x cm，AG=y cm，
∴DG² + AD²=AG²，即(3 - y)² + x²=y²，与Rt△BCE中方程相同，
∵FH=0时，点F与点H重合，即$\sqrt{9+x^{2}} - 2x=0$，
解得$x=\sqrt{3}$(负值舍去)，
∴当BC的长为$\sqrt{3}$ cm时，四边形AECG是菱形。

【变式二】如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接AF,CE.
(1)求证：四边形AFCE为菱形；

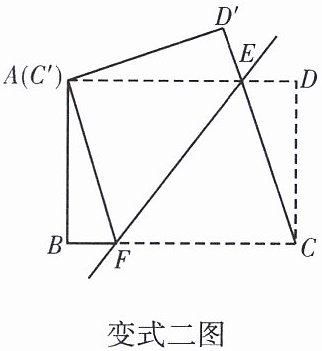
(2)设AE= a,ED= b,DC= c. 求证：$a^2= b^2+c^2.$

答案：
(1)证明：
∵矩形ABCD沿EF折叠，点C与点A重合，
∴OA=OC，EF⊥AC，AE=CE，AF=CF，
∵AD//BC，
∴∠AEO=∠CFO，
在△AOE和△COF中，
∠AEO=∠CFO，∠AOE=∠COF，OA=OC，
∴△AOE≌△COF(AAS)，
∴AE=CF，
∵AE=CE，AF=CF，
∴AE=CE=CF=AF，
∴四边形AFCE为菱形；
(2)证明：
∵四边形ABCD是矩形，
∴∠D=90°，
∵AE=a，ED=b，
∴AD=AE+ED=a+b，
∵四边形AFCE为菱形，
∴CE=AE=a，
在Rt△CDE中，CE²=ED²+DC²，
∴a²=b²+c²．