《2025年一本通武汉出版社九年级数学上册北师大版核心板》

8. 如图,在矩形 ABCD 中,∠BEF= 90°,则一定相似的三角形是 ………………… (B)
A.①和②
B.①和③
C.②和③
D.③和④

答案： 【解析】：
本题可根据矩形的性质以及相似三角形的判定条件来判断哪两个三角形一定相似。
在矩形$ABCD$中，$\angle A=\angle D = 90^{\circ}$，又因为$\angle BEF = 90^{\circ}$，所以$\angle AEB+\angle DEF = 90^{\circ}$。
在$\triangle ABE$中，$\angle ABE+\angle AEB = 90^{\circ}$，由此可得$\angle ABE=\angle DEF$。
因为$\angle A=\angle D$，$\angle ABE=\angle DEF$，根据两角分别相等的两个三角形相似，可知$\triangle ABE\sim\triangle DEF$，即图中的①和③相似。
逐一分析选项：
选项A：①是$\triangle ABE$，②是$\triangle EBF$，仅根据已知条件无法得出这两个三角形相似，所以该选项错误。
选项B：由前面的推理可知①$\triangle ABE$和③$\triangle DEF$相似，所以该选项正确。
选项C：②是$\triangle EBF$，③是$\triangle DEF$，仅根据已知条件无法得出这两个三角形相似，所以该选项错误。
选项D：③是$\triangle DEF$，④是$\triangle CFE$，仅根据已知条件无法得出这两个三角形相似，所以该选项错误。
【答案】：B

9. 如图,在四边形 ABCD 中,AB//CD,∠C= 90°,∠BDA= 90°,AB= a,BD= b,CD= c,BC= d,AD= e,则下列等式成立的是 ………………………………………………… (A)
A.$b^2= ac$
B.$b^2= ce$
C.be= ac
D.bd= ae

答案： 【解析】：
由于AB//CD，∠C= 90°，∠BDA= 90°，
可以得到两个直角三角形：△BCD和△DBA，
这两个三角形在∠BDC和∠DBA处都是直角，
且由于AB//CD，所以∠CBD=∠DBA（内错角相等），
因此，△BCD∽△DBA（AA相似），
根据相似三角形的性质，对应边成比例，即：$\frac{CD}{BD} = \frac{BD}{AB}$，
代入已知的边长，得到：$\frac{c}{b} = \frac{b}{a}$，
进一步整理，可以得到：$b^2 = ac$。
【答案】：A.$b^2= ac$。

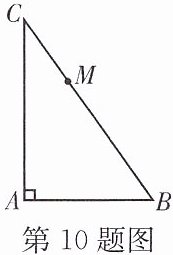
10. 如图,点 M 是 Rt△ABC 的斜边 BC 上异于 B,C 的一定点,过点 M 作直线截△ABC,使截得的三角形与△ABC 相似,这样的直线共有3条.

答案： 【解析】：本题主要考查三角形相似的判定条件。
过点M作直线$MN// AB$，交$AC$于点N，
由于$MN// AB$，
根据平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似，
所以$\bigtriangleup CMN\sim \bigtriangleup CBA$。
过点M作直线$MP// AC$，交$AB$于点P，
由于$MP// AC$，
同理可得$\bigtriangleup BMP\sim \bigtriangleup BCA$。
过点M分别作$AC$，$AB$的垂线$MD$，$ME$，垂足分别为D，E，
由于$\angle MDC=\angle MEB=90^\circ$，且$\angle C=\angle C$，$\angle B=\angle B$（公共角），
根据两角对应相等的两个三角形相似，
所以$\bigtriangleup CMD\sim \bigtriangleup CAB$，$\bigtriangleup BME\sim \bigtriangleup BCA$。
因此，这样的直线共有3种可能，但每种可能都对应两条直线（除了与直角边垂直的情况，它只对应一条直线但算作两种截法中的一种），
但由于与直角边垂直的直线算作一种截法，且它与其他情况不重复，
所以总共有3条不同的直线满足条件。
【答案】：3。

11. (24 西宁)【感知特例】(1)如图 1,点 A,B 在直线 l 上,AC⊥l,DB⊥l,垂足分别为 A,B,点 P 在线段 AB 上,且 PC⊥PD,垂足为 P. 结论：AC·BD= AP·BP.
证明：∵AC⊥l,BD⊥l,PC⊥PD,
∴∠CAP= ∠DBP= ∠CPD= 90°,
∴∠C+∠APC= 90°,
∠D+∠APC= 90°,
∴∠C= ∠D(同角的余角相等),
∴△APC∽△BDP(两角分别相等的两个三角形相似),
∴$\frac{AC}{BP}$= $\frac{AP}{BD}$(相似三角形对应边成比例),
即 AC·BD= AP·BP.
【建构模型】(2)如图 2,点 A,B 在直线 l 上,点 P 在线段 AB 上,且∠CAP= ∠DBP= ∠CPD,结论 AC·BD= AP·BP 仍成立吗？请说明理由.
(2) 成立，理由如下：
证明：∵∠CAP=∠DBP=∠CPD，
∴∠APC+∠C=180°-∠CAP，∠APC+∠DPB=180°-∠CPD，
∴∠C=∠DPB，
∴△APC∽△BDP（两角分别相等的两个三角形相似），
∴$\frac{AC}{BP}=\frac{AP}{BD}$（相似三角形对应边成比例），
即AC·BD=AP·BP
【解决问题】(3)如图 3,在△ABC 中,AC= BC= 5,AB= 8,点 P 和点 D 分别是线段 AB,BC 上的动点,始终满足∠CPD= ∠A. 设 AP 长为 x(0＜x＜8),当 x= 4 时,BD= $\frac{7}{5}$.

答案：
(1) ∠D；∠C；∠D；同角的余角相等；△BDP；两角分别相等的两个三角形相似；$\frac{AC}{BP}$；$\frac{AP}{BD}$；相似三角形对应边成比例
(2) 成立，理由如下：
证明：
∵∠CAP=∠DBP=∠CPD，
∴∠APC+∠C=180°-∠CAP，∠APC+∠DPB=180°-∠CPD，
∴∠C=∠DPB，
∴△APC∽△BDP（两角分别相等的两个三角形相似），
∴$\frac{AC}{BP}=\frac{AP}{BD}$（相似三角形对应边成比例），
即AC·BD=AP·BP
(3)$\frac{7}{5}$