《2025年一本通武汉出版社九年级数学上册北师大版核心板》

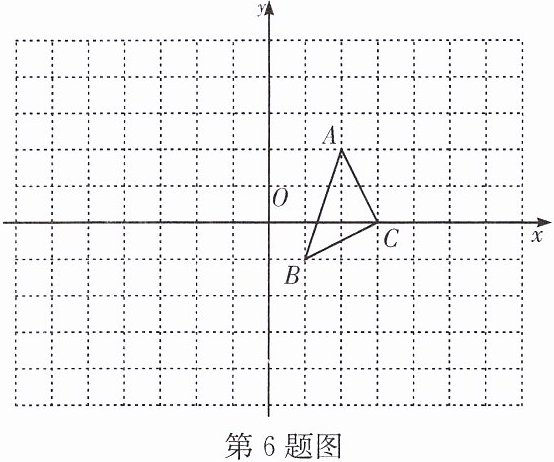
6. 如图,已知$A(2,2)$,$B(1,-1)$,$C(3,0)$.
(1)画出以点O为位似中心,将$\triangle ABC$放大到原来2倍的$\triangle A'B'C'$;
(2)分别写出$\triangle A'B'C'$三个顶点的坐标.

答案：
(1) 图略（分别在点O同侧和异侧画出放大2倍的位似图形）
(2) 情况一（同侧）：$A'(4,4)$，$B'(2,-2)$，$C'(6,0)$
情况二（异侧）：$A'(-4,-4)$，$B'(-2,2)$，$C'(-6,0)$

7. 如图,点D,E,F分别是$\triangle ABC(AB＞AC)$各边的中点,下列说法不正确的是 ………… (A)
A.AD平分$\angle BAC$
B.EF与AD相互平分
C.$2EF= BC$
D.$\triangle DEF是\triangle ABC$的位似图形

答案： 【解析】：本题可根据三角形中位线定理、相似三角形的判定与性质以及位似图形的定义来逐一分析选项。
选项A：
三角形中位线定理：三角形的中位线平行于三角形的第三边，并且等于第三边的一半。
已知点$D$，$E$，$F$分别是$\triangle ABC$各边的中点，仅根据这些条件，无法得出$AD$平分$\angle BAC$。
因为$AD$平分$\angle BAC$需要满足$\angle BAD = \angle CAD$，而题中并没有给出能证明这两个角相等的条件，所以该选项说法不正确。
选项B：
因为点$D$，$E$，$F$分别是$\triangle ABC$各边的中点，所以$DE$，$EF$，$DF$是$\triangle ABC$的中位线。
根据三角形中位线定理可得$DE// AC$，$EF// AB$，则四边形$AEDF$是平行四边形（两组对边分别平行的四边形是平行四边形）。
而平行四边形的对角线互相平分，$AD$与$EF$是平行四边形$AEDF$的对角线，所以$EF$与$AD$相互平分，该选项说法正确。
选项C：
由于$EF$是$\triangle ABC$的中位线，根据三角形中位线定理：三角形的中位线平行于三角形的第三边，并且等于第三边的一半，可得$EF=\frac{1}{2}BC$，即$2EF = BC$，该选项说法正确。
选项D：
位似图形的定义：如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形。
因为点$D$，$E$，$F$分别是$\triangle ABC$各边的中点，所以$\triangle DEF\sim\triangle ABC$（三边对应成比例的两个三角形相似），且$\frac{DE}{AC}=\frac{EF}{AB}=\frac{DF}{BC}=\frac{1}{2}$。
同时，连接$AF$，$BD$，$CE$，它们相交于一点（三角形的重心），并且$\triangle DEF$与$\triangle ABC$的对应边互相平行（由中位线定理可知），满足位似图形的定义，所以$\triangle DEF$是$\triangle ABC$的位似图形，该选项说法正确。
【答案】：A

8. 如图是一个简易的幻灯机,幻灯片与屏幕平行,光源到幻灯片的距离是30 cm,幻灯片到屏幕的距离是1.5 m,幻灯片上小树的高度是10 cm,则屏幕上小树的高度是 …………………… (C)
A.50 cm
B.500 cm
C.60 cm
D.600 cm

答案： 【解析】：本题可根据相似三角形的性质来求解屏幕上小树的高度。
由于幻灯片与屏幕平行，光源发出的光线形成的两个三角形是相似的。
相似三角形对应边成比例，设屏幕上小树的高度是$x cm$。
已知光源到幻灯片的距离是$30cm$，幻灯片到屏幕的距离是$1.5m = 150cm$，幻灯片上小树的高度是$10cm$。
根据相似三角形对应边成比例可得：$\frac{10}{x}=\frac{30}{30 + 150}$。
【答案】：
解：设屏幕上小树的高度是$x cm$。
因为$1.5m = 150cm$，由相似三角形对应边成比例可得：
$\frac{10}{x}=\frac{30}{30 + 150}$
$\frac{10}{x}=\frac{30}{180}$
$\frac{10}{x}=\frac{1}{6}$
$x = 60$
所以屏幕上小树的高度是$60cm$，答案选C。

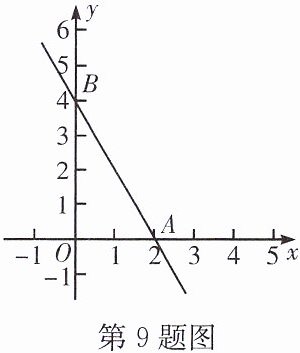
9. 如果两个一次函数$y= k_1x+b_1和y= k_2x+b_2满足k_1= k_2$,$b_1\neq b_2$,那么称这两个一次函数为"平行一次函数".如图,已知函数$y= -2x+4$的图象与x轴,y轴分别交于A,B两点,一次函数$y= kx+b与y= -2x+4$是"平行一次函数".
(1)若函数$y= kx+b$的图象过点(3,1),求b的值;
(2)若函数$y= kx+b的图象与两坐标轴围成的三角形和\triangle AOB$构成位似图形,位似中心为原点,位似比为1:2,求函数$y= kx+b$的表达式.

答案：
(1)解：因为一次函数$y=kx+b$与$y=-2x+4$是“平行一次函数”，所以$k=-2$，则函数为$y=-2x+b$。
又因为函数$y=-2x+b$的图象过点$(3,1)$，将$x=3$，$y=1$代入$y=-2x+b$，得$1=-2×3+b$，解得$b=7$。
(2)解：对于函数$y=-2x+4$，当$y=0$时，$0=-2x+4$，解得$x=2$，所以$A(2,0)$；当$x=0$时，$y=4$，所以$B(0,4)$。
因为函数$y=kx+b$与$y=-2x+4$是“平行一次函数”，所以$k=-2$，函数为$y=-2x+b$。
设函数$y=-2x+b$与$x$轴交于点$C(m,0)$，与$y$轴交于点$D(0,n)$。
当$y=0$时，$0=-2m+b$，解得$m=\frac{b}{2}$，所以$C(\frac{b}{2},0)$；当$x=0$时，$y=b$，所以$D(0,b)$。
因为$\triangle COD$和$\triangle AOB$构成位似图形，位似中心为原点，位似比为$1:2$。
情况一：位似图形在位似中心同侧，所以$\frac{OC}{OA}=\frac{OD}{OB}=\frac{1}{2}$。
$OA=2$，$OB=4$，则$OC=\frac{1}{2}OA=1$，$OD=\frac{1}{2}OB=2$。
所以$|\frac{b}{2}|=1$，$|b|=2$。因为同侧，$b$与$4$同号，所以$b=2$，函数表达式为$y=-2x+2$。
情况二：位似图形在位似中心两侧，所以$\frac{OC}{OA}=\frac{OD}{OB}=\frac{1}{2}$，但坐标符号相反。
则$OC=\frac{1}{2}OA=1$，$OD=\frac{1}{2}OB=2$，但$C$、$D$在坐标轴负半轴，所以$|\frac{b}{2}|=1$，$|b|=2$，此时$b=-2$，函数表达式为$y=-2x-2$。
综上，函数$y=-2x+b$的表达式为$y=-2x+2$或$y=-2x-2$。