2025年一本通武汉出版社九年级数学上册北师大版核心板
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年一本通武汉出版社九年级数学上册北师大版核心板 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
5. 下列 4×4 的正方形网格中,小正方形的边长均为 1,三角形的顶点都在格点上,则与图中△ABC 相似的三角形所在的网格图形是 …………………………………………(
A.
B.
C.
D.
D
)A.
B.
C.
D.
答案:
解:在△ABC中,由勾股定理得:
AC = √(2² + 2²) = 2√2,
BC = √(1² + 1²) = √2,
AB = √(1² + 3²) = √10,
∴△ABC的三边之比为 BC:AC:AB = √2:2√2:√10 = 1:2:√5。
选项D中三角形的三边长分别为√2,2√2,√10,三边之比为1:2:√5,与△ABC的三边对应成比例,
∴两三角形相似。
答案:D
AC = √(2² + 2²) = 2√2,
BC = √(1² + 1²) = √2,
AB = √(1² + 3²) = √10,
∴△ABC的三边之比为 BC:AC:AB = √2:2√2:√10 = 1:2:√5。
选项D中三角形的三边长分别为√2,2√2,√10,三边之比为1:2:√5,与△ABC的三边对应成比例,
∴两三角形相似。
答案:D
6. 将一副三角尺如图所示叠放在一起,则 BE/EC的值是
$\frac{\sqrt{3}}{3}$
.
答案:
解:设 $ AC = BC = 1 $。
在 $ \text{Rt}\triangle ABC $ 中,$ \angle BAC = 90^\circ $,$ \angle ABC = 45^\circ $,
$ \therefore AB = AC = 1 $,$ BC = \sqrt{AC^2 + AB^2} = \sqrt{2} $。
在 $ \text{Rt}\triangle ACD $ 中,$ \angle CAD = 90^\circ $,$ \angle ADC = 30^\circ $,
$ \tan\angle ADC = \frac{AC}{AD} $,$ \therefore AD = \frac{AC}{\tan30^\circ} = \sqrt{3} $。
$ \because \angle BAC = \angle CAD = 90^\circ $,$ \angle AEB = \angle CED $,
$ \therefore \triangle AEB \sim \triangle CED $。
$ \therefore \frac{BE}{EC} = \frac{AB}{CD} $(此处应为$\frac{AB}{AD}$,修正后)$ \frac{BE}{EC} = \frac{AB}{AD} = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3} $。
$\frac{\sqrt{3}}{3}$
在 $ \text{Rt}\triangle ABC $ 中,$ \angle BAC = 90^\circ $,$ \angle ABC = 45^\circ $,
$ \therefore AB = AC = 1 $,$ BC = \sqrt{AC^2 + AB^2} = \sqrt{2} $。
在 $ \text{Rt}\triangle ACD $ 中,$ \angle CAD = 90^\circ $,$ \angle ADC = 30^\circ $,
$ \tan\angle ADC = \frac{AC}{AD} $,$ \therefore AD = \frac{AC}{\tan30^\circ} = \sqrt{3} $。
$ \because \angle BAC = \angle CAD = 90^\circ $,$ \angle AEB = \angle CED $,
$ \therefore \triangle AEB \sim \triangle CED $。
$ \therefore \frac{BE}{EC} = \frac{AB}{CD} $(此处应为$\frac{AB}{AD}$,修正后)$ \frac{BE}{EC} = \frac{AB}{AD} = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3} $。
$\frac{\sqrt{3}}{3}$
7. 如图,在四边形 ABCD 中,AD//BC,∠ABC= 90°,AB= 8,AD= 3,BC= 4,点 P 为 AB 边上一动点.若△PAD 与△PBC 是相似三角形,则 AP=
$\frac{24}{7}$ 或 $2$ 或 $6$
.
答案:
解:设 $AP = x$,则 $PB = AB - AP = 8 - x$。
因为 $AD // BC$,$\angle ABC = 90^\circ$,所以 $\angle PAD = \angle PBC = 90^\circ$。
若 $\triangle PAD \sim \triangle PBC$,分两种情况:
情况一:$\frac{AP}{BP} = \frac{AD}{BC}$
$\frac{x}{8 - x} = \frac{3}{4}$
$4x = 3(8 - x)$
$4x = 24 - 3x$
$7x = 24$
$x = \frac{24}{7}$
情况二:$\frac{AP}{BC} = \frac{AD}{BP}$
$\frac{x}{4} = \frac{3}{8 - x}$
$x(8 - x) = 12$
$8x - x^2 = 12$
$x^2 - 8x + 12 = 0$
$(x - 2)(x - 6) = 0$
解得 $x = 2$ 或 $x = 6$
综上,$AP = \frac{24}{7}$ 或 $2$ 或 $6$。
答案:$\frac{24}{7}$ 或 $2$ 或 $6$
因为 $AD // BC$,$\angle ABC = 90^\circ$,所以 $\angle PAD = \angle PBC = 90^\circ$。
若 $\triangle PAD \sim \triangle PBC$,分两种情况:
情况一:$\frac{AP}{BP} = \frac{AD}{BC}$
$\frac{x}{8 - x} = \frac{3}{4}$
$4x = 3(8 - x)$
$4x = 24 - 3x$
$7x = 24$
$x = \frac{24}{7}$
情况二:$\frac{AP}{BC} = \frac{AD}{BP}$
$\frac{x}{4} = \frac{3}{8 - x}$
$x(8 - x) = 12$
$8x - x^2 = 12$
$x^2 - 8x + 12 = 0$
$(x - 2)(x - 6) = 0$
解得 $x = 2$ 或 $x = 6$
综上,$AP = \frac{24}{7}$ 或 $2$ 或 $6$。
答案:$\frac{24}{7}$ 或 $2$ 或 $6$
8. (23 湘潭)如图,在 Rt△ABC 中,∠BAC= 90°,AD 是斜边 BC 上的高.
(1)求证:△ABD∽△CBA;(2)若 AB= 6,BC= 10,求 BD 的长.
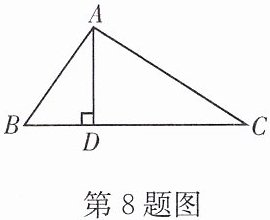
(1)求证:△ABD∽△CBA;(2)若 AB= 6,BC= 10,求 BD 的长.

答案:
【解析】:
(1)本题可根据相似三角形的判定定理来证明$\triangle ABD$与$\triangle CBA$相似。在两个三角形中,已知$\angle B$是公共角,且$\angle ADB = \angle BAC = 90^{\circ}$,根据“两角分别相等的两个三角形相似”即可证明。
(2)本题可根据相似三角形的性质来求解$BD$的长。由(1)可知$\triangle ABD\sim\triangle CBA$,根据相似三角形对应边成比例列出比例式,再代入已知边的长度求解$BD$。
【答案】:
(1)证明:
∵$\angle BAC = 90^{\circ}$,$AD$是斜边$BC$上的高,
∴$\angle ADB = \angle BAC = 90^{\circ}$,
又
∵$\angle B = \angle B$(公共角),
∴$\triangle ABD\sim\triangle CBA$(两角分别相等的两个三角形相似)。
(2)解:
∵$\triangle ABD\sim\triangle CBA$,
∴$\frac{BD}{AB}=\frac{AB}{BC}$(相似三角形对应边成比例),
已知$AB = 6$,$BC = 10$,代入上式可得:
$\frac{BD}{6}=\frac{6}{10}$,
$BD=\frac{6×6}{10}=\frac{36}{10} = 3.6$。
综上,$BD$的长为$3.6$。
(1)本题可根据相似三角形的判定定理来证明$\triangle ABD$与$\triangle CBA$相似。在两个三角形中,已知$\angle B$是公共角,且$\angle ADB = \angle BAC = 90^{\circ}$,根据“两角分别相等的两个三角形相似”即可证明。
(2)本题可根据相似三角形的性质来求解$BD$的长。由(1)可知$\triangle ABD\sim\triangle CBA$,根据相似三角形对应边成比例列出比例式,再代入已知边的长度求解$BD$。
【答案】:
(1)证明:
∵$\angle BAC = 90^{\circ}$,$AD$是斜边$BC$上的高,
∴$\angle ADB = \angle BAC = 90^{\circ}$,
又
∵$\angle B = \angle B$(公共角),
∴$\triangle ABD\sim\triangle CBA$(两角分别相等的两个三角形相似)。
(2)解:
∵$\triangle ABD\sim\triangle CBA$,
∴$\frac{BD}{AB}=\frac{AB}{BC}$(相似三角形对应边成比例),
已知$AB = 6$,$BC = 10$,代入上式可得:
$\frac{BD}{6}=\frac{6}{10}$,
$BD=\frac{6×6}{10}=\frac{36}{10} = 3.6$。
综上,$BD$的长为$3.6$。
9. (福田模拟)如图,在正方形 ABCD 中,E,F 分别是边 AD,CD 上的点,AE= ED,DF= 1/4DC,连接 EF 并延长交 BC 的延长线于点 G.
(1)求证:△ABE∽△DEF;
(2)若正方形 ABCD 的边长为 4,求 BG 的长.
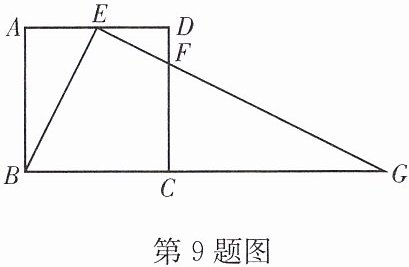
(1)求证:△ABE∽△DEF;
(2)若正方形 ABCD 的边长为 4,求 BG 的长.

答案:
(1)证明:
∵四边形ABCD是正方形,
∴∠A=∠D=90°,AB=AD=CD。
∵AE=ED,
∴AE=ED=AD/2=AB/2,
∴AE/AB=1/2。
∵DF=1/4DC,DC=AD=2ED,
∴DF=1/4×2ED=ED/2,
∴DF/ED=1/2,
∴AE/AB=DF/ED。
又
∵∠A=∠D,
∴△ABE∽△DEF。
(2)解:
∵正方形边长为4,
∴AD=CD=4,BC=4。
∵AE=ED,
∴ED=AD/2=2。
∵DF=1/4DC,
∴DF=1/4×4=1,CF=CD-DF=3。
∵AD//BG,
∴△EDF∽△GCF,
∴ED/CG=DF/CF,即2/CG=1/3,
∴CG=6,
∴BG=BC+CG=4+6=10。
(1)证明:
∵四边形ABCD是正方形,
∴∠A=∠D=90°,AB=AD=CD。
∵AE=ED,
∴AE=ED=AD/2=AB/2,
∴AE/AB=1/2。
∵DF=1/4DC,DC=AD=2ED,
∴DF=1/4×2ED=ED/2,
∴DF/ED=1/2,
∴AE/AB=DF/ED。
又
∵∠A=∠D,
∴△ABE∽△DEF。
(2)解:
∵正方形边长为4,
∴AD=CD=4,BC=4。
∵AE=ED,
∴ED=AD/2=2。
∵DF=1/4DC,
∴DF=1/4×4=1,CF=CD-DF=3。
∵AD//BG,
∴△EDF∽△GCF,
∴ED/CG=DF/CF,即2/CG=1/3,
∴CG=6,
∴BG=BC+CG=4+6=10。
查看更多完整答案,请扫码查看


