《2025年一本通武汉出版社九年级数学上册北师大版核心板》

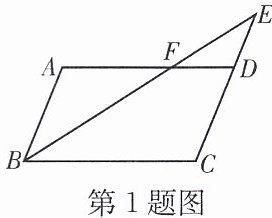
1. 如图,四边形 ABCD 是平行四边形,则图中与△DEF 相似的三角形是△CEB.

答案： 【解析】：本题可根据平行四边形的性质以及相似三角形的判定定理来找出与$\triangle DEF$相似的三角形。
已知四边形$ABCD$是平行四边形，则$AD// BC$，$AB// CD$。
因为$AD// BC$，所以$\angle EDF = \angle EBC$（两直线平行，内错角相等），$\angle E$为公共角。
根据两角分别相等的两个三角形相似，可得$\triangle DEF\sim\triangle CEB$。
【答案】：$\triangle CEB$

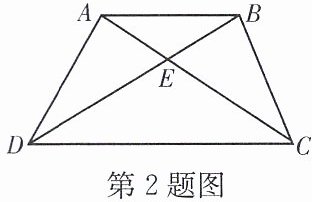
2. 如图,在四边形 ABCD 中,AB//CD,BD 与 AC 交于点 E,△AED 与△BEC 相似吗？有如下解答：
证明：∵AB//CD,
∴∠ABE= ∠CDE,∠BAE= ∠DCE.
∴△AEB∽△CED,∴AE/DE= BE/CE
又∵∠AED= ∠BEC,∴△AED∽△BEC.
请判断解答是否正确,并说明理由.

答案： 【解析】：本题考查相似三角形的判定定理，该解答试图通过先证明$\triangle AEB$和$\triangle CED$相似，进而推导出$\frac{AE}{DE}=\frac{BE}{CE}$，再结合$\angle AED=\angle BEC$来证明$\triangle AED$和$\triangle BEC$相似。然而，这种方法存在逻辑上的错误，因为相似三角形的对应边成比例和对应角相等是同时满足的，不能通过一个三角形的相似性来推导出另一个三角形的相似性，除非这两个三角形有直接的相似关系或者通过其他方式证明它们的对应边成比例和对应角相等。
正确的证明方法应该是直接利用相似三角形的判定定理，如两边成比例且夹角相等，或者两角对应相等。在本题中，由于$AB// CD$，可以得到$\angle ABE=\angle CDE$和$\angle BAE=\angle DCE$，但这只能证明$\triangle AEB$和$\triangle CED$相似，不能直接证明$\triangle AED$和$\triangle BEC$相似。
实际上，要证明$\triangle AED$和$\triangle BEC$相似，需要利用平行线分线段成比例定理，得到$\frac{AE}{CE}=\frac{DE}{BE}$，再结合$\angle AED=\angle BEC$（对顶角相等），才能根据相似三角形的判定定理得出$\triangle AED\sim\triangle BEC$。
因此，该解答的逻辑推理是错误的。
【答案】：不正确，见解析

3. 如图,在△ABC 中,点 D,E 分别在 AB,AC 上,AD·AB= AE·AC.
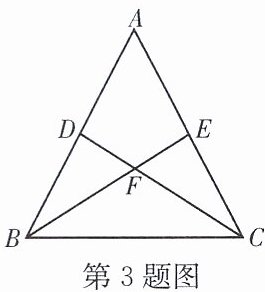
求证:(1)△ABE∽△ACD；(2)FD·FC= FB·FE.

答案： 【解析】：
本题主要考查相似三角形的判定定理以及相似三角形对应边成比例的性质。
对于（1），需要证明两个三角形相似，根据已知条件$AD\cdot AB = AE\cdot AC$，通过变形得到对应边的比例关系，再结合公共角来证明$\triangle ABE$与$\triangle ACD$相似。
对于（2），由（1）得出相似三角形后，利用相似三角形对应边成比例得到比例式，然后通过交叉相乘来证明$FD\cdot FC = FB\cdot FE$。
【答案】：
证明：
(1)
∵$AD\cdot AB = AE\cdot AC$，
∴$\frac{AD}{AC}=\frac{AE}{AB}$。
又
∵$\angle A$是$\triangle ABE$与$\triangle ACD$的公共角，即$\angle A = \angle A$。
根据“两边成比例且夹角相等的两个三角形相似”，
∴$\triangle ABE\sim\triangle ACD$。
(2)
由（1）知$\triangle ABE\sim\triangle ACD$，
∴$\angle B = \angle C$。
∵$\angle BFD$与$\angle CFE$是对顶角，
∴$\angle BFD = \angle CFE$。
∴$\triangle BFD\sim\triangle CFE$。
∴$\frac{FD}{FE}=\frac{FB}{FC}$。
交叉相乘可得$FD\cdot FC = FB\cdot FE$。

4. 如图是边长为 1 的小正方形组成的网格,△ABC 的顶点都在网格点上.
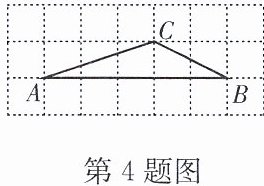
(1)在 AB 上找出格点 P,连接 PC,当 BP= 时,△BCP∽△BAC；
(2)利用"三边对应成比例的两个三角形相似"证明(1)中结论.

答案：