2025年一本通武汉出版社九年级数学上册北师大版核心板
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年一本通武汉出版社九年级数学上册北师大版核心板 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1.(龙华模拟)如图,某中学有一块长30 m,宽20 m的矩形空地,计划在这块空地上划出三分之二的区域种花,设花带的宽度为x m,则可列方程为 …………………………………………………………………… (
A.(30-x)(20-x)= 2/3×20×30
B.(30-2x)(20-x)= 1/3×20×30
C.30x+2×20x= 1/3×20×30
D.(30-2x)(20-x)= 2/3×20×30
B
)A.(30-x)(20-x)= 2/3×20×30
B.(30-2x)(20-x)= 1/3×20×30
C.30x+2×20x= 1/3×20×30
D.(30-2x)(20-x)= 2/3×20×30
答案:
解:矩形空地面积为 $30×20$ 平方米,种花区域面积为 $\frac{2}{3}×30×20$ 平方米。
由图可知,未种花区域为矩形,其长为 $30 - 2x$ 米,宽为 $20 - x$ 米,未种花区域面积为 $(30 - 2x)(20 - x)$ 平方米。
因为种花区域面积占三分之二,所以未种花区域面积占三分之一,即 $(30 - 2x)(20 - x) = \frac{1}{3}×30×20$。
答案:B
由图可知,未种花区域为矩形,其长为 $30 - 2x$ 米,宽为 $20 - x$ 米,未种花区域面积为 $(30 - 2x)(20 - x)$ 平方米。
因为种花区域面积占三分之二,所以未种花区域面积占三分之一,即 $(30 - 2x)(20 - x) = \frac{1}{3}×30×20$。
答案:B
2.如图,在Rt△ABC中,∠C= 90°,点P,Q同时由A,B两点出发,分别沿AC,BC方向向点C匀速移动,速度都是1 m/s.x s后△PCQ的面积为Rt△ACB面积的一半,下面所列方程正确的是……………………………………………… (
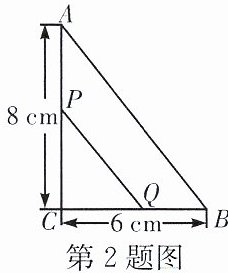
A.1/2(8-x)(6-x)= 1/2×8×6×1/2
B.1/2(8-x)(6-x)= 1/2×8×6
C.1/2(8-x)(6-x)= 8×6
D.1/2(8-x)(6-x)= 2×8×6
A
)
A.1/2(8-x)(6-x)= 1/2×8×6×1/2
B.1/2(8-x)(6-x)= 1/2×8×6
C.1/2(8-x)(6-x)= 8×6
D.1/2(8-x)(6-x)= 2×8×6
答案:
【解析】:本题可先分别表示出$PC$、$CQ$的长度,再根据三角形面积公式表示出$\triangle PCQ$的面积,最后结合已知条件列出方程。
步骤一:求出$AC$、$BC$的长度以及$\triangle ABC$的面积
已知在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 8cm$,$BC = 6cm$。
根据直角三角形面积公式$S=\frac{1}{2}ab$(其中$a$、$b$为直角边),可得$\triangle ABC$的面积为:
$S_{\triangle ABC}=\frac{1}{2}× AC× BC=\frac{1}{2}× 8× 6$ $cm^2$。
步骤二:求出$PC$、$CQ$的长度
因为点$P$、$Q$同时由$A$、$B$两点出发,速度都是$1m/s$,$x s$后,$AP = x m$,$BQ = x m$。
那么$PC = AC - AP = (8 - x)cm$,$CQ = BC - BQ = (6 - x)cm$。
步骤三:求出$\triangle PCQ$的面积
同样根据直角三角形面积公式,可得$\triangle PCQ$的面积为:
$S_{\triangle PCQ}=\frac{1}{2}× PC× CQ=\frac{1}{2}(8 - x)(6 - x)$ $cm^2$。
步骤四:根据已知条件列出方程
已知$x s$后$\triangle PCQ$的面积为$Rt\triangle ACB$面积的一半,即$S_{\triangle PCQ}=\frac{1}{2}S_{\triangle ABC}$。
将$S_{\triangle ABC}=\frac{1}{2}× 8× 6$,$S_{\triangle PCQ}=\frac{1}{2}(8 - x)(6 - x)$代入$S_{\triangle PCQ}=\frac{1}{2}S_{\triangle ABC}$,可得:
$\frac{1}{2}(8 - x)(6 - x)=\frac{1}{2}×\frac{1}{2}× 8× 6$,化简后为$\frac{1}{2}(8 - x)(6 - x)=\frac{1}{2}× 8× 6×\frac{1}{2}$。
【答案】:A
步骤一:求出$AC$、$BC$的长度以及$\triangle ABC$的面积
已知在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 8cm$,$BC = 6cm$。
根据直角三角形面积公式$S=\frac{1}{2}ab$(其中$a$、$b$为直角边),可得$\triangle ABC$的面积为:
$S_{\triangle ABC}=\frac{1}{2}× AC× BC=\frac{1}{2}× 8× 6$ $cm^2$。
步骤二:求出$PC$、$CQ$的长度
因为点$P$、$Q$同时由$A$、$B$两点出发,速度都是$1m/s$,$x s$后,$AP = x m$,$BQ = x m$。
那么$PC = AC - AP = (8 - x)cm$,$CQ = BC - BQ = (6 - x)cm$。
步骤三:求出$\triangle PCQ$的面积
同样根据直角三角形面积公式,可得$\triangle PCQ$的面积为:
$S_{\triangle PCQ}=\frac{1}{2}× PC× CQ=\frac{1}{2}(8 - x)(6 - x)$ $cm^2$。
步骤四:根据已知条件列出方程
已知$x s$后$\triangle PCQ$的面积为$Rt\triangle ACB$面积的一半,即$S_{\triangle PCQ}=\frac{1}{2}S_{\triangle ABC}$。
将$S_{\triangle ABC}=\frac{1}{2}× 8× 6$,$S_{\triangle PCQ}=\frac{1}{2}(8 - x)(6 - x)$代入$S_{\triangle PCQ}=\frac{1}{2}S_{\triangle ABC}$,可得:
$\frac{1}{2}(8 - x)(6 - x)=\frac{1}{2}×\frac{1}{2}× 8× 6$,化简后为$\frac{1}{2}(8 - x)(6 - x)=\frac{1}{2}× 8× 6×\frac{1}{2}$。
【答案】:A
3.一直角三角形两条直角边长的和为7,面积为6,求斜边的长.
答案:
解:设一条直角边长为$x$,则另一条直角边长为$7 - x$。
根据题意,得$\frac{1}{2}x(7 - x) = 6$,
整理,得$x^2 - 7x + 12 = 0$,
解得$x_1 = 3$,$x_2 = 4$。
当$x = 3$时,另一条直角边长为$7 - 3 = 4$;
当$x = 4$时,另一条直角边长为$7 - 4 = 3$。
所以两直角边长分别为3和4。
根据勾股定理,斜边长为$\sqrt{3^2 + 4^2} = 5$。
答:斜边的长为5。
根据题意,得$\frac{1}{2}x(7 - x) = 6$,
整理,得$x^2 - 7x + 12 = 0$,
解得$x_1 = 3$,$x_2 = 4$。
当$x = 3$时,另一条直角边长为$7 - 3 = 4$;
当$x = 4$时,另一条直角边长为$7 - 4 = 3$。
所以两直角边长分别为3和4。
根据勾股定理,斜边长为$\sqrt{3^2 + 4^2} = 5$。
答:斜边的长为5。
4.如图,在Rt△ABC中,∠C= 90°,AC= 30 cm,BC= 25 cm.动点P从点C出发,沿CA方向运动,速度是2 cm/s;动点Q从点B出发,沿BC方向运动,速度是1 cm/s.
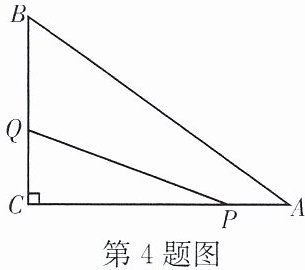
(1)若设运动时间为x s,则图中的线段CP=
(2)几秒后,△PCQ为等腰三角形?
(3)几秒后,P,Q两点相距25 cm?

(1)若设运动时间为x s,则图中的线段CP=
2x cm
,PA=(30 - 2x)cm
,BQ=x cm
,QC=(25 - x)cm
.(2)几秒后,△PCQ为等腰三角形?
解:当△PCQ是等腰三角形时,CP = CQ,即2x = 25 - x,x=25/3,∴25/3s后,△PCQ是等腰三角形。
(3)几秒后,P,Q两点相距25 cm?
解:当P,Q两点相距25cm时,(2x)²+(25 - x)²=25²,4x²+625 - 50x + x²=625,5x²-50x = 0,5x(x - 10)=0,x = 0(舍)或x = 10,∴10s后P,Q两点相距25cm。
答案:
【解析】:
本题主要考查一元二次方程的应用,通过动点问题设立未知数,再根据等腰三角形的性质以及勾股定理列出方程求解。
(1)已知动点$P$从点$C$出发,速度是$2cm/s$,运动时间为$x s$,根据路程$=$速度$×$时间,可得$CP = 2x cm$。
因为$AC = 30cm$,所以$PA=(30 - 2x)cm$。
动点$Q$从点$B$出发,速度是$1cm/s$,运动时间为$x s$,则$BQ = x cm$。
又因为$BC = 25cm$,所以$QC=(25 - x)cm$。
(2)当$\triangle PCQ$为等腰三角形时,$CP = CQ$,即$2x = 25 - x$,移项可得$2x + x = 25$,$3x = 25$,解得$x=\frac{25}{3}$。
(3)在$Rt\triangle PCQ$中,根据勾股定理$PC^{2}+QC^{2}=PQ^{2}$,已知$PQ = 25cm$,$PC = 2x cm$,$QC=(25 - x)cm$,则可列出方程$(2x)^{2}+(25 - x)^{2}=25^{2}$。
展开式子得$4x^{2}+625 - 50x + x^{2}=625$,
合并同类项得$5x^{2}-50x = 0$,提取公因式$5x$得$5x(x - 10)=0$,
则$5x = 0$或$x - 10 = 0$,解得$x = 0$(舍去,因为$x = 0$时,动点刚开始运动,不符合题意)或$x = 10$。
【答案】:
(1)$2x cm$;$(30 - 2x)cm$;$x cm$;$(25 - x)cm$
(2)解:当$\triangle PCQ$是等腰三角形时,$CP = CQ$,
即$2x = 25 - x$,$x=\frac{25}{3}$,
$\therefore\frac{25}{3}s$后,$\triangle PCQ$是等腰三角形。
(3)解:当$P$,$Q$两点相距$25cm$时,
$(2x)^{2}+(25 - x)^{2}=25^{2}$
$4x^{2}+625 - 50x + x^{2}=625$
$5x^{2}-50x = 0$
$5x(x - 10)=0$
$x = 0$(舍)或$x = 10$
$\therefore 10s$后$P$,$Q$两点相距$25cm$。
本题主要考查一元二次方程的应用,通过动点问题设立未知数,再根据等腰三角形的性质以及勾股定理列出方程求解。
(1)已知动点$P$从点$C$出发,速度是$2cm/s$,运动时间为$x s$,根据路程$=$速度$×$时间,可得$CP = 2x cm$。
因为$AC = 30cm$,所以$PA=(30 - 2x)cm$。
动点$Q$从点$B$出发,速度是$1cm/s$,运动时间为$x s$,则$BQ = x cm$。
又因为$BC = 25cm$,所以$QC=(25 - x)cm$。
(2)当$\triangle PCQ$为等腰三角形时,$CP = CQ$,即$2x = 25 - x$,移项可得$2x + x = 25$,$3x = 25$,解得$x=\frac{25}{3}$。
(3)在$Rt\triangle PCQ$中,根据勾股定理$PC^{2}+QC^{2}=PQ^{2}$,已知$PQ = 25cm$,$PC = 2x cm$,$QC=(25 - x)cm$,则可列出方程$(2x)^{2}+(25 - x)^{2}=25^{2}$。
展开式子得$4x^{2}+625 - 50x + x^{2}=625$,
合并同类项得$5x^{2}-50x = 0$,提取公因式$5x$得$5x(x - 10)=0$,
则$5x = 0$或$x - 10 = 0$,解得$x = 0$(舍去,因为$x = 0$时,动点刚开始运动,不符合题意)或$x = 10$。
【答案】:
(1)$2x cm$;$(30 - 2x)cm$;$x cm$;$(25 - x)cm$
(2)解:当$\triangle PCQ$是等腰三角形时,$CP = CQ$,
即$2x = 25 - x$,$x=\frac{25}{3}$,
$\therefore\frac{25}{3}s$后,$\triangle PCQ$是等腰三角形。
(3)解:当$P$,$Q$两点相距$25cm$时,
$(2x)^{2}+(25 - x)^{2}=25^{2}$
$4x^{2}+625 - 50x + x^{2}=625$
$5x^{2}-50x = 0$
$5x(x - 10)=0$
$x = 0$(舍)或$x = 10$
$\therefore 10s$后$P$,$Q$两点相距$25cm$。
查看更多完整答案,请扫码查看


