《2025年一本通武汉出版社九年级数学上册北师大版核心板》

【变式三】如图,有一正方形的纸片ABCD,边长为3,点E是DC边上一点,且DE= 1/3DC,把△ADE沿AE折叠,使△ADE落在△AFE的位置,延长EF交BC边于点G,连接AG.
(1)求∠GAE的度数；

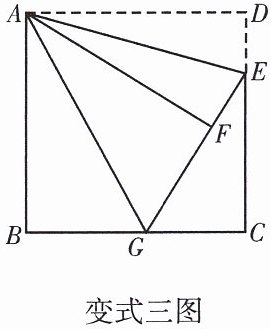
(2)求证：BG+DE= GE；
(3)求证：BG= CG；
(4)求S△ECG.

答案： 【解析】：
(1)本题可根据正方形的性质、折叠的性质以及全等三角形的判定和性质来求解$\angle GAE$的度数。
先根据正方形边长和$DE$与$DC$的关系求出$DE$、$EC$的长度，再通过证明$\triangle ADG\cong\triangle AFG$得到$\angle DAG = \angle FAG$，结合$\angle DAF$是由$\triangle ADE$折叠得到，进而求出$\angle GAE$的度数。
(2)本题可通过证明$\triangle ABG\cong\triangle AFG$，得到$BG = FG$，再结合$EF = DE$，从而证明$BG + DE = GE$。
(3)本题可通过设未知数，利用勾股定理建立方程来证明$BG = CG$。
设$BG = x$，表示出$CG$、$EG$的长度，在$Rt\triangle ECG$中根据勾股定理列出方程，求解得到$BG$与$CG$的关系。
(4)本题可先求出$CG$、$EG$的长度，再根据三角形面积公式求出$S_{\triangle ECG}$。
【答案】：
(1)
解：
$\because$四边形$ABCD$是边长为$3$的正方形，
$\therefore AD = AB = BC = CD = 3$，$\angle D=\angle B=\angle BCD = 90^{\circ}$。
$\because DE=\frac{1}{3}DC$，
$\therefore DE = 1$，$EC = 2$。
由折叠可知：$\triangle ADE\cong\triangle AFE$，
$\therefore\angle D=\angle AFE = \angle AFG = 90^{\circ}$，$AD = AF$，$\angle DAE = \angle FAE$。
$\because AD = AB$，
$\therefore AF = AB$。
在$Rt\triangle ABG$和$Rt\triangle AFG$中
$\begin{cases}AG = AG\\AB = AF\end{cases}$
$\therefore Rt\triangle ABG\cong Rt\triangle AFG(HL)$，
$\therefore\angle BAG = \angle FAG$。
$\because\angle DAE+\angle FAE+\angle FAG+\angle BAG = 90^{\circ}$，
$\therefore 2\angle FAE + 2\angle FAG = 90^{\circ}$，
$\therefore\angle GAE = \angle FAE + \angle FAG = 45^{\circ}$。
(2)
证明：
由
(1)可知$Rt\triangle ABG\cong Rt\triangle AFG$，
$\therefore BG = FG$。
$\because\triangle ADE\cong\triangle AFE$，
$\therefore DE = EF$。
$\because GE = EF + FG$，
$\therefore GE = DE + BG$，
即$BG + DE = GE$。
(3)
证明：
设$BG = x$，则$CG = 3 - x$，$GE = EF + FG = DE + BG = 1 + x$。
在$Rt\triangle ECG$中，根据勾股定理$EC^{2}+CG^{2}=GE^{2}$，
即$2^{2}+(3 - x)^{2}=(1 + x)^{2}$，
$4 + 9 - 6x + x^{2}=1 + 2x + x^{2}$，
$13 - 6x = 1 + 2x$，
$8x = 12$，
解得$x = \frac{3}{2}$。
$\therefore CG = 3 - \frac{3}{2}=\frac{3}{2}$，
$\therefore BG = CG$。
(4)
解：
由
(3)可知$CG = \frac{3}{2}$，$EG = 1 + \frac{3}{2}=\frac{5}{2}$，$EC = 2$。
$\therefore S_{\triangle ECG}=\frac{1}{2}× EC× CG=\frac{1}{2}× 2×\frac{3}{2}=\frac{3}{2}$。

【变式四】如图,在正方形ABCD中,点E为BC上一点,连接DE,把△DEC沿DE折叠得到△DEF,延长EF交AB于点G,连接DG.
(1)当点E为BC的中点时,连接BF.

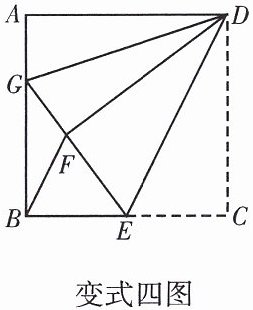
①求证：BF//DE；
②若正方形的边长为6,求线段AG的长.
(2)当BE∶EC=2∶1时,DE= DG.

答案：
(1)①证明：
∵△DEC沿DE折叠得到△DEF，
∴DC=DF，∠CDE=∠FDE，∠C=∠DFE=90°。
∵四边形ABCD是正方形，
∴AD=DC=BC，∠ADC=∠C=90°，
∴AD=DF。
在Rt△ADG和Rt△FDG中，AD=DF，DG=DG，
∴Rt△ADG≌Rt△FDG（HL），
∴∠ADG=∠FDG。
设∠CDE=∠FDE=x，则∠ADG=∠FDG=(90°-2x)/2=45°-x，
∴∠GDE=∠FDG+∠FDE=45°。
∵E为BC中点，BC=6，
∴EC=EF=3，BE=3。设AG=FG=y，则BG=6-y，GE=3+y。
在Rt△BGE中，BG²+BE²=GE²，即(6-y)²+3²=(3+y)²，解得y=2，
∴AG=2，BG=4。
∵BE=EF=3，
∴∠EBF=∠EFB。
∵∠GEB=∠EBF+∠EFB=2∠EBF，∠GEB=180°-∠GED-∠FED=180°-45°-∠CDE=135°-x，∠CDE=x，∠DEC=90°-x，
∴∠FED=∠DEC=90°-x，
∴∠GEB=180°-∠GED-∠FED=180°-45°-(90°-x)=45°+x，
∴135°-x=45°+x，解得x=45°，
∴∠EBF=(135°-45°)/2=45°，
∴∠EBF=∠GDE=45°，
∴BF//DE。
②解：由①得AG=2。
(2)解：设BE∶EC=k，设EC=a，则BE=ka，BC=DC=DF=(k+1)a。
由折叠知EF=EC=a，∠DFE=90°。设AG=FG=b，则BG=(k+1)a-b，GE=a+b。
在Rt△BGE中，BG²+BE²=GE²，即[(k+1)a-b]²+(ka)²=(a+b)²，化简得b=(k²a)/2(k+1)。
∵DE=DG，DE²=DC²+EC²=(k+1)²a²+a²=(k²+2k+2)a²，DG²=AD²+AG²=(k+1)²a²+b²，
∴(k²+2k+2)a²=(k+1)²a²+[k⁴a²/4(k+1)²]，化简得k⁴-4k²-4k=0，k(k³-4k-4)=0，解得k=2（k＞0），
∴BE∶EC=2∶1。
答案：
(1)①见证明；②2；
(2)2∶1。