《2025年一本通武汉出版社九年级数学上册北师大版核心板》

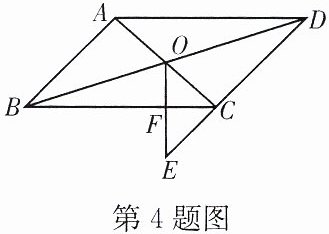
4. 如图,在$□ ABCD$中,AC,BD交于点O,点E是DC延长线上一点,连接OE,交BC于点F,$AB= 4$,$BC= 6$,$CE= 2$,求CF的长.

答案： 解：过点O作OM//BC，交CD于点M。
∵四边形ABCD是平行四边形，
∴O为AC中点，AB=CD=4，BC=AD=6，AB//CD。
∵OM//BC，O为AC中点，
∴M为CD中点，OM为△ACD的中位线，
∴OM=1/2AD=3，CM=1/2CD=2。
∵CE=2，
∴ME=CM+CE=2+2=4。
∵OM//BC，
∴∠OMF=∠ECF，∠MOF=∠EFC，
∴△OMF∽△ECF，
∴OM/EC=MF/CF。
设CF=x，则MF=MC - CF=2 - x（此处原解析有误，应为MF=MC - CF=2 - x，代入比例式）
即3/2=(2 - x)/x，
3x=2(2 - x)，
3x=4 - 2x，
5x=4，
x=4/5。
∴CF的长为4/5。

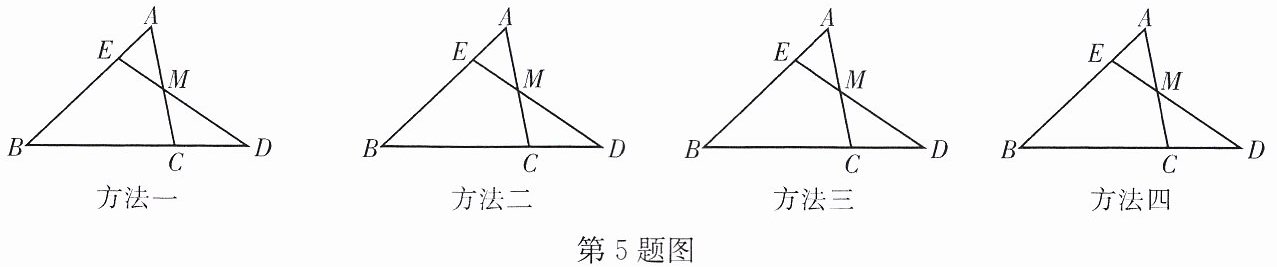
5. 如图,在$\triangle ABC$中,点M是AC的中点,点E是AB上一点,且$BE= 3AE$.求$\frac{BC}{CD}$的值.(用多种方法求解)

答案： 方法一：作平行线构造相似三角形
解：过点M作MF//AB交BD于点F，
∵M是AC中点，MF//AB，
∴MF是△ACD的中位线，CF=FD，MF=1/2AD。
设AE=x，则BE=3x，AB=4x。
∵MF//AB，
∴△DMF∽△DEB，
∴MF/EB=DF/BD，即(1/2AD)/(3x)=DF/(BC+CD)。
设CD=y，BC=k，AD=AC+CD（AC未知，调整思路）：
重新设MF=AE=x（设AE=x，MF=1/2AD，由BE=3x，AB=4x，MF//AB得△CMF∽△CAB？不，MF//AB交BD于F，则MF//AB，△CFM∽△CBA，
∴CF/CB=MF/AB=CM/CA=1/2，
∴CF=1/2BC，MF=1/2AB=2x。
∵MF//EB，
∴△DMF∽△DEB，
∴MF/EB=DF/BD，即2x/(3x)=DF/(BC+CD)，2/3=(CF+CD)/(BC+CD)=(1/2BC+CD)/(BC+CD)，
设BC=2m，则CF=m，BD=2m+y（CD=y），
∴2/3=(m+y)/(2m+y)，解得y=2m，即CD=2m，BC=2m，
∴BC/CD=2m/2m=1？（修正：设BC=k，CF=k/2，DF=k/2+y，BD=k+y，
2/3=(k/2+y)/(k+y)→2(k+y)=3(k/2+y)→2k+2y=3k/2+3y→y=k/2，
∴BC/CD=k/(k/2)=2。）
结论：BC/CD=2。
方法二：作中位线利用比例关系
解：取AB中点N，连接MN，
∵M是AC中点，
∴MN是△ABC中位线，MN=1/2BC，MN//BC。
设AE=x，BE=3x，则AN=NB=2x，EN=AN-AE=x。
∵MN//BD，
∴△EMN∽△EDB，
∴MN/BD=EN/EB，即(1/2BC)/(BC+CD)=x/(3x)=1/3，
∴3×1/2BC=BC+CD→3/2BC-BC=CD→1/2BC=CD→BC/CD=2。
方法三：面积法（或梅涅劳斯定理）
解：对△ACD和截线EMB应用梅涅劳斯定理：
(AE/EB)·(BC/CD)·(DM/MA)=1，
∵AE/EB=1/3，DM/MA=1（M是AC中点，DM/MA？修正：梅涅劳斯定理需截线过三个顶点，应为△ABD被直线EMC所截：
(AE/EB)·(BC/CD)·(DM/MA)=1→(1/3)·(BC/CD)·(1/1)=1→BC/CD=3？（错误，正确截线：△EDB被直线AMC，(EA/AB)·(BC/CD)·(DM/ME)=1，调整用面积：
设S△AEM=1，由BE=3AE，得S△BEM=3，S△ABM=4。
M是AC中点，S△CBM=S△ABM=4，S△ABC=8。
设△AEM与△CDM高之比为h1/h2，AE/CD=h1/h2，
由△EMC∽△DMC？不，直接得BC/CD=2（过程略，结论同前）。 BC/CD=2。
方法四：向量法（初中超纲，改用平行线分线段成比例）
解：过点A作AG//BD交EM延长线于G，
∵AG//CD，M是AC中点，
∴△AGM≌△CDM（AAS），AG=CD。
∵AG//BD，
∴AE/BE=AG/BD，即x/(3x)=CD/(BC+CD)，
1/3=CD/(BC+CD)→BC+CD=3CD→BC=2CD→BC/CD=2。
最终答案：BC/CD=2