2025年一本通武汉出版社九年级数学上册北师大版核心板
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年一本通武汉出版社九年级数学上册北师大版核心板 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
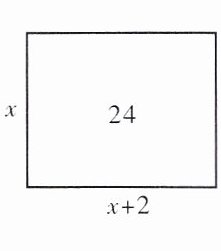
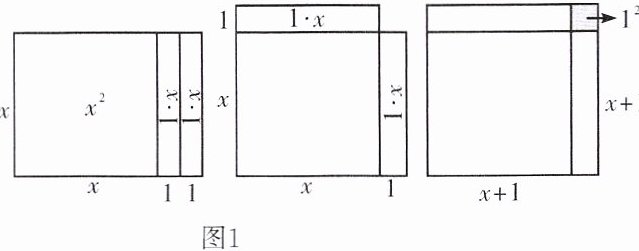
2.【示范操作】方法1:用配方法解一元二次方程$x^{2}+2x-24= 0$,变形为$x(x+2)= 24$,将配方的过程转化为图形的“割”“拼”“补”,如图1.
得$(x+1)^{2}= 24+1^{2}$.
方法2:古代数学家赵爽著《勾股圆方图注》中的配方方法更加简捷,只用了“拼”完成了配方,用4个长为$x+2$,宽为$x$,面积为24的长方形,拼成如图2的大正方形,利用大正方形的面积等于4个长方形的面积加中空的小正方形面积,得$(x+x+2)^{2}= 4×24+2^{2}$.
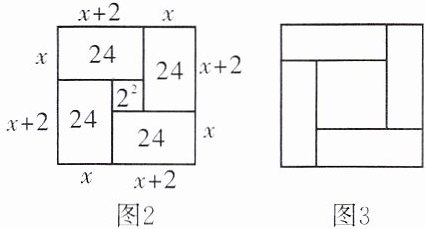
【模仿实践】(1)仿方法2配方解$x^{2}+5x-14= 0$,先变形为______,如图3,每个小长方形的长为______,宽为______,利用图形的面积关系得配方后的方程为______,解为______.
【深入探究】(2)仿方法2配方解$2x^{2}+5x= 3$,自己画图分析,写出解题过程.
【总结提升】(3)小敏同学质疑方法2的局限性:$x^{2}+5x+3= 0$,变形为$x(x+5)= -3$,没法拼图了呀?
小聪同学发现:方法2中的拼图就是$(a+b)^{2}= 4ab+(a-b)^{2}$模型,于是有了方法3.设$x= a$,$x+5= b$,则有$\begin{cases}ab= -3,\\a-b= -5.\end{cases} 则(a+b)^{2}= 4×(-3)+(-5)^{2}$,$(x+x+5)^{2}= 13$,配方成功,从数到形,又从形回归到数.请你用小聪的方法3配方解$x^{2}-7x+2= 0$,写出解题过程.
得$(x+1)^{2}= 24+1^{2}$.
方法2:古代数学家赵爽著《勾股圆方图注》中的配方方法更加简捷,只用了“拼”完成了配方,用4个长为$x+2$,宽为$x$,面积为24的长方形,拼成如图2的大正方形,利用大正方形的面积等于4个长方形的面积加中空的小正方形面积,得$(x+x+2)^{2}= 4×24+2^{2}$.


【模仿实践】(1)仿方法2配方解$x^{2}+5x-14= 0$,先变形为______,如图3,每个小长方形的长为______,宽为______,利用图形的面积关系得配方后的方程为______,解为______.

【深入探究】(2)仿方法2配方解$2x^{2}+5x= 3$,自己画图分析,写出解题过程.
【总结提升】(3)小敏同学质疑方法2的局限性:$x^{2}+5x+3= 0$,变形为$x(x+5)= -3$,没法拼图了呀?
小聪同学发现:方法2中的拼图就是$(a+b)^{2}= 4ab+(a-b)^{2}$模型,于是有了方法3.设$x= a$,$x+5= b$,则有$\begin{cases}ab= -3,\\a-b= -5.\end{cases} 则(a+b)^{2}= 4×(-3)+(-5)^{2}$,$(x+x+5)^{2}= 13$,配方成功,从数到形,又从形回归到数.请你用小聪的方法3配方解$x^{2}-7x+2= 0$,写出解题过程.
答案:
$(1)$ 答案
- 变形为$x(x + 5)=14$;
- 每个小长方形的长为$x + 5$,宽为$x$;
- 配方后的方程为$(x+x + 5)^{2}=4×14+5^{2}$;
- 解为$x_{1}=2,x_{2}=-7$。
$(2)$ 解题过程
解:将方程$2x^{2}+5x = 3$两边同时除以$2$,得$x^{2}+\frac{5}{2}x=\frac{3}{2}$,变形为$x(x+\frac{5}{2})=\frac{3}{2}$。
设小长方形长为$x+\frac{5}{2}$,宽为$x$,用$4$个这样的长方形拼大正方形。
根据大正方形的面积等于$4$个长方形的面积加中空小正方形面积,可得$(x+x+\frac{5}{2})^{2}=4×\frac{3}{2}+(\frac{5}{2})^{2}$。
即$(2x+\frac{5}{2})^{2}=6+\frac{25}{4}=\frac{24 + 25}{4}=\frac{49}{4}$。
则$2x+\frac{5}{2}=\pm\frac{7}{2}$。
当$2x+\frac{5}{2}=\frac{7}{2}$时,$2x=\frac{7}{2}-\frac{5}{2}=1$,$x=\frac{1}{2}$;
当$2x+\frac{5}{2}=-\frac{7}{2}$时,$2x=-\frac{7}{2}-\frac{5}{2}=-6$,$x=-3$。
$(3)$ 解题过程
解:对于方程$x^{2}-7x + 2=0$,变形为$x(x - 7)=-2$。
设$x=a$,$x - 7=b$,则$\begin{cases}ab=-2\\a - b=7\end{cases}$。
根据$(a + b)^{2}=4ab+(a - b)^{2}$,可得$(x+x - 7)^{2}=4×(-2)+7^{2}$。
即$(2x - 7)^{2}=-8 + 49=41$。
则$2x-7=\pm\sqrt{41}$。
当$2x-7=\sqrt{41}$时,$2x=7+\sqrt{41}$,$x=\frac{7+\sqrt{41}}{2}$;
当$2x-7=-\sqrt{41}$时,$2x=7-\sqrt{41}$,$x=\frac{7-\sqrt{41}}{2}$。
综上,$(1)$答案依次为$x(x + 5)=14$;$x + 5$;$x$;$(x+x + 5)^{2}=4×14+5^{2}$;$x_{1}=2,x_{2}=-7$;$(2)$方程的解为$x_{1}=\frac{1}{2},x_{2}=-3$;$(3)$方程的解为$x_{1}=\frac{7+\sqrt{41}}{2},x_{2}=\frac{7-\sqrt{41}}{2}$。
- 变形为$x(x + 5)=14$;
- 每个小长方形的长为$x + 5$,宽为$x$;
- 配方后的方程为$(x+x + 5)^{2}=4×14+5^{2}$;
- 解为$x_{1}=2,x_{2}=-7$。
$(2)$ 解题过程
解:将方程$2x^{2}+5x = 3$两边同时除以$2$,得$x^{2}+\frac{5}{2}x=\frac{3}{2}$,变形为$x(x+\frac{5}{2})=\frac{3}{2}$。
设小长方形长为$x+\frac{5}{2}$,宽为$x$,用$4$个这样的长方形拼大正方形。
根据大正方形的面积等于$4$个长方形的面积加中空小正方形面积,可得$(x+x+\frac{5}{2})^{2}=4×\frac{3}{2}+(\frac{5}{2})^{2}$。
即$(2x+\frac{5}{2})^{2}=6+\frac{25}{4}=\frac{24 + 25}{4}=\frac{49}{4}$。
则$2x+\frac{5}{2}=\pm\frac{7}{2}$。
当$2x+\frac{5}{2}=\frac{7}{2}$时,$2x=\frac{7}{2}-\frac{5}{2}=1$,$x=\frac{1}{2}$;
当$2x+\frac{5}{2}=-\frac{7}{2}$时,$2x=-\frac{7}{2}-\frac{5}{2}=-6$,$x=-3$。
$(3)$ 解题过程
解:对于方程$x^{2}-7x + 2=0$,变形为$x(x - 7)=-2$。
设$x=a$,$x - 7=b$,则$\begin{cases}ab=-2\\a - b=7\end{cases}$。
根据$(a + b)^{2}=4ab+(a - b)^{2}$,可得$(x+x - 7)^{2}=4×(-2)+7^{2}$。
即$(2x - 7)^{2}=-8 + 49=41$。
则$2x-7=\pm\sqrt{41}$。
当$2x-7=\sqrt{41}$时,$2x=7+\sqrt{41}$,$x=\frac{7+\sqrt{41}}{2}$;
当$2x-7=-\sqrt{41}$时,$2x=7-\sqrt{41}$,$x=\frac{7-\sqrt{41}}{2}$。
综上,$(1)$答案依次为$x(x + 5)=14$;$x + 5$;$x$;$(x+x + 5)^{2}=4×14+5^{2}$;$x_{1}=2,x_{2}=-7$;$(2)$方程的解为$x_{1}=\frac{1}{2},x_{2}=-3$;$(3)$方程的解为$x_{1}=\frac{7+\sqrt{41}}{2},x_{2}=\frac{7-\sqrt{41}}{2}$。
查看更多完整答案,请扫码查看


