2025年一本通武汉出版社九年级数学上册北师大版核心板
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年一本通武汉出版社九年级数学上册北师大版核心板 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
如果两个相似多边形任意一组对应顶点P,P'所在的直线都经过同一点O,且有
$\frac{OP}{OP'}=k$
$(k\neq0)$,那么这样的两个多边形叫做位似多边形,点O叫做位似中心
,k就是这两个多边形的相似比.
答案:
$\frac{OP}{OP'}=k$;位似中心
1. 在如图所示的四个图案中,位似图形有 …………………………………………… (
A.1个
B.2个
C.3个
D.4个
C
)A.1个
B.2个
C.3个
D.4个
答案:
C
2. 如图,两个三角形是位似图形,它们的位似中心是 ……………………………… (
A.点P
B.点O
C.点M
D.点N
A
)A.点P
B.点O
C.点M
D.点N
答案:
解:位似图形的对应点连线交于位似中心。观察图形,连接两个三角形的对应顶点,其连线交于点P。
答案:A
答案:A
3. 如图,将$\triangle ABC的三边缩小到原来的\frac{1}{2}$,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,得到$\triangle DEF$,则下列说法错误的是 …………………………………………… (
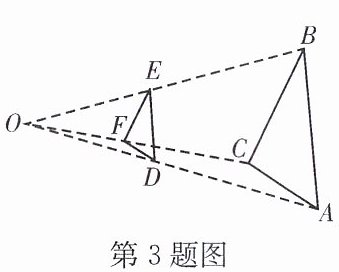
A.$\triangle ABC与\triangle DEF$是位似图形
B.$\triangle ABC与\triangle DEF$是相似图形
C.$\triangle ABC与\triangle DEF$的面积之比为4:1
D.$\triangle ABC与\triangle DEF$的周长之比为1:2
D
)
A.$\triangle ABC与\triangle DEF$是位似图形
B.$\triangle ABC与\triangle DEF$是相似图形
C.$\triangle ABC与\triangle DEF$的面积之比为4:1
D.$\triangle ABC与\triangle DEF$的周长之比为1:2
答案:
【解析】:本题可根据位似图形、相似图形的定义以及相似三角形的性质来逐一分析选项。
选项A:判断$\triangle ABC$与$\triangle DEF$是否为位似图形
位似图形的定义为:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形。
在本题中,任取一点$O$,$\triangle ABC$的三边缩小到原来的$\frac{1}{2}$得到$\triangle DEF$,且$D$,$E$,$F$分别是$AO$,$BO$,$CO$的中点,所以$\triangle ABC$与$\triangle DEF$对应顶点的连线相交于点$O$,对应边互相平行,满足位似图形的定义,因此$\triangle ABC$与$\triangle DEF$是位似图形,该选项正确。
选项B:判断$\triangle ABC$与$\triangle DEF$是否为相似图形
相似图形的定义为:形状相同的图形叫做相似图形。
由于$\triangle DEF$是将$\triangle ABC$的三边缩小到原来的$\frac{1}{2}$得到的,所以$\triangle ABC$与$\triangle DEF$的形状相同,满足相似图形的定义,因此$\triangle ABC$与$\triangle DEF$是相似图形,该选项正确。
选项C:求$\triangle ABC$与$\triangle DEF$的面积之比
相似三角形面积比等于相似比的平方。
已知$\triangle DEF$是将$\triangle ABC$的三边缩小到原来的$\frac{1}{2}$得到的,所以$\triangle ABC$与$\triangle DEF$的相似比为$2:1$,那么它们的面积之比为$2^2:1^2 = 4:1$,该选项正确。
选项D:求$\triangle ABC$与$\triangle DEF$的周长之比
相似三角形周长比等于相似比。
因为$\triangle ABC$与$\triangle DEF$的相似比为$2:1$,所以它们的周长之比为$2:1$,而不是$1:2$,该选项错误。
【答案】:D
选项A:判断$\triangle ABC$与$\triangle DEF$是否为位似图形
位似图形的定义为:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形。
在本题中,任取一点$O$,$\triangle ABC$的三边缩小到原来的$\frac{1}{2}$得到$\triangle DEF$,且$D$,$E$,$F$分别是$AO$,$BO$,$CO$的中点,所以$\triangle ABC$与$\triangle DEF$对应顶点的连线相交于点$O$,对应边互相平行,满足位似图形的定义,因此$\triangle ABC$与$\triangle DEF$是位似图形,该选项正确。
选项B:判断$\triangle ABC$与$\triangle DEF$是否为相似图形
相似图形的定义为:形状相同的图形叫做相似图形。
由于$\triangle DEF$是将$\triangle ABC$的三边缩小到原来的$\frac{1}{2}$得到的,所以$\triangle ABC$与$\triangle DEF$的形状相同,满足相似图形的定义,因此$\triangle ABC$与$\triangle DEF$是相似图形,该选项正确。
选项C:求$\triangle ABC$与$\triangle DEF$的面积之比
相似三角形面积比等于相似比的平方。
已知$\triangle DEF$是将$\triangle ABC$的三边缩小到原来的$\frac{1}{2}$得到的,所以$\triangle ABC$与$\triangle DEF$的相似比为$2:1$,那么它们的面积之比为$2^2:1^2 = 4:1$,该选项正确。
选项D:求$\triangle ABC$与$\triangle DEF$的周长之比
相似三角形周长比等于相似比。
因为$\triangle ABC$与$\triangle DEF$的相似比为$2:1$,所以它们的周长之比为$2:1$,而不是$1:2$,该选项错误。
【答案】:D
4. 如图,$\triangle ABC与\triangle A'B'C'$是位似图形,且位似比是1:2.若$AB= 2\ \text{cm}$,则$A'B'= $
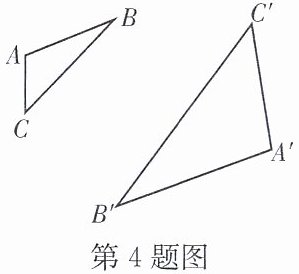
4
cm,请在图中画出位似中心O
答案:
【解析】:
本题考查的是位似图形的性质。
位似图形指的是两个图形不仅是相似图形,而且每组对应的点之间的连线都相交于一点,即位似中心。
位似比定义为对应边之间的比例。
由题意知,$\triangle ABC$与$\triangle A'B'C'$是位似图形,且位似比是$1:2$。
根据位似比,可以知道对应边的长度比也是$1:2$。
因为给定了$AB = 2 \text{cm}$,所以可以根据位似比计算出$A'B'$的长度。
$A'B' = AB × 2 = 2 \text{cm} × 2 = 4 \text{cm}$
对于位似中心的确定,由于位似中心是对应点连线的交点,可以通过延长$AB$和$A'B'$,找到它们的交点,即为位似中心$O$。
【答案】:
$A'B' = 4 \text{cm}$
位似中心$O$的确定:图略(可以通过延长$AB$和$A'B'$找到交点$O$)
本题考查的是位似图形的性质。
位似图形指的是两个图形不仅是相似图形,而且每组对应的点之间的连线都相交于一点,即位似中心。
位似比定义为对应边之间的比例。
由题意知,$\triangle ABC$与$\triangle A'B'C'$是位似图形,且位似比是$1:2$。
根据位似比,可以知道对应边的长度比也是$1:2$。
因为给定了$AB = 2 \text{cm}$,所以可以根据位似比计算出$A'B'$的长度。
$A'B' = AB × 2 = 2 \text{cm} × 2 = 4 \text{cm}$
对于位似中心的确定,由于位似中心是对应点连线的交点,可以通过延长$AB$和$A'B'$,找到它们的交点,即为位似中心$O$。
【答案】:
$A'B' = 4 \text{cm}$
位似中心$O$的确定:图略(可以通过延长$AB$和$A'B'$找到交点$O$)
5. 如图,$\triangle OAB$的顶点都在格点上,请在网格中画出$\triangle OAB$的一个位似图形,使两个图形以点O为位似中心,且所画图形与$\triangle OAB$的位似比为2:1.
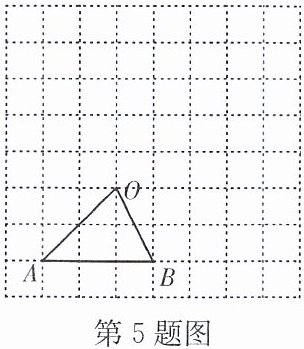

答案:
解:
1. 连接OA并延长至点A',使OA' = 2OA;
2. 连接OB并延长至点B',使OB' = 2OB;
3. 连接A'B',则△OA'B'即为所求位似图形。
(注:图形需在网格中按上述步骤画出,A'、B'分别为OA、OB延长线上距O两倍原长的格点。)
1. 连接OA并延长至点A',使OA' = 2OA;
2. 连接OB并延长至点B',使OB' = 2OB;
3. 连接A'B',则△OA'B'即为所求位似图形。
(注:图形需在网格中按上述步骤画出,A'、B'分别为OA、OB延长线上距O两倍原长的格点。)
查看更多完整答案,请扫码查看


