《2025年一本通武汉出版社九年级数学上册北师大版核心板》

6. (24西藏)如图,在Rt△ABC中,∠C= 90°,AC= 12,BC= 5,点P是边AB上任意一点,过点P作PD⊥AC,PE⊥BC,垂足分别为点D,E,连接DE,则DE的最小值是$\frac{60}{13}$.

答案： 解：在Rt△ABC中，∠C=90°，AC=12，BC=5，
由勾股定理得AB=$\sqrt{AC^2 + BC^2}=\sqrt{12^2 + 5^2}=13$。
∵PD⊥AC，PE⊥BC，∠C=90°，
∴四边形DCEP是矩形，
∴DE=CP。
当CP⊥AB时，CP最小。
∵S_{△ABC}=$\frac{1}{2}$AC·BC=$\frac{1}{2}$AB·CP，
∴CP=$\frac{AC·BC}{AB}=\frac{12×5}{13}=\frac{60}{13}$。
∴DE的最小值是$\frac{60}{13}$。
$\frac{60}{13}$

7. 小明参加了检测雕塑底座正面四边形ABCD(如图)是不是一个矩形的实践活动.
【实践测量】小明用卷尺测量AD= BC= 60厘米,AB= CD= 80厘米,对角线BD= 100厘米.
【探究验证】(1)小明通过计算验证四边形ABCD是一个矩形,请你写出他的验证过程；
【问题解决】(2)爱脑筋的小华同学说如果卷尺是没有刻度的,他也有办法检验四边形ABCD是不是矩形.请写出小华的检验方法并说明理由.

答案：
(1)证明：
∵AD=BC=60厘米，AB=CD=80厘米，
∴四边形ABCD是平行四边形。在△ABD中，AD²+AB²=60²+80²=3600+6400=10000，BD²=100²=10000，
∴AD²+AB²=BD²，
∴∠A=90°，
∴平行四边形ABCD是矩形。
(2)检验方法：用无刻度卷尺分别测量四边形ABCD的两组对边是否相等，再测量两条对角线是否相等。理由：若两组对边分别相等，则四边形是平行四边形；若平行四边形的对角线相等，则该平行四边形是矩形。

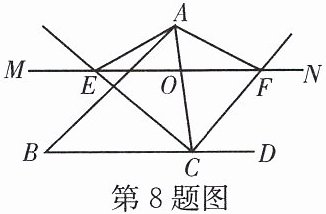
8. 如图,在△ABC中,O是边AC上一个动点,过点O作直线MN//BC.设MN交∠ACB的平分线于点E,交∠ACB外角的平分线于点F.
(1)求证:OE= OF；
(2)若CE= 12,CF= 5,求OC的长；
(3)连接AE,AF,当点O运动到什么位置时,四边形AECF是矩形？并说明理由.

答案： 【解析】：
(1)证明：
∵MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F，
∴∠2=∠5，∠4=∠6，
∵MN//BC，
∴∠1=∠5，∠3=∠6，
∴∠1=∠2，∠3=∠4，
∴EO=CO，FO=CO，
∴OE=OF。
(2)
∵CE，CF分别是∠ACB及∠ACB的外角的平分线，
∴∠ECF是直角三角形，
∵$OE=OF，OC=OE=OF$，
∴由勾股定理可得$EF= \sqrt{12^2+5^2}=13$，
∴$OC= \frac{1}{2}EF=6.5$。
(3)当点O运动到AC的中点时，四边形AECF是矩形。
理由如下：
连接AE，AF，当O为AC的中点时，$AO=CO$，
∵$EO=FO$，
∴四边形AECF是平行四边形，
∵$∠ECF=90^\circ$，
∴四边形AECF是矩形。
【答案】：
(1)证明见解析；
(2)$OC=6.5$；
(3)当点O运动到AC的中点时，四边形AECF是矩形，理由见解析。